4.1: Basic Definitions
- Page ID
- 19042
( \newcommand{\kernel}{\mathrm{null}\,}\)
We shall now consider functions whose domains and ranges are sets in some fixed (but otherwise arbitrary) metric spaces (S,ρ) and (T,ρ′), respectively. We write
f:A→(T,ρ′)
for a function f with Df=A⊆(S,ρ) and D′f⊆(T,ρ′).S is called the domain space, and T the range space, of f.
I. Given such a function, we often have to investigate its "local behavior" near some point p∈S. In particular, if p∈A=Df( so that f(p) is defined) we may ask: Is it possible to make the function values f(x) as near as we like ("ε− near") to f(p) by keeping x sufficiently close ( "close ′′) to p, i.e., inside some sufficiently small globe Gp(δ)? If this is the case, we say that f is continuous at p. More precisely, we formulate the following definition.
A function f:A→(T,ρ′), with A⊆(S,ρ), is said to be continuous at p iff p∈A and, moreover, for each ε>0 (no matter how small) there is δ>0 such that ρ′(f(x),f(p))<ε for all x∈A∩Gp(δ). In symbols,
(∀ε>0)(∃δ>0)(∀x∈A∩Gp(δ)){ρ′(f(x),f(p))<ε, or f(x)∈Gf(p)(ε)
If (1) fails, we say that f is discontinuous at p and call p a discontinuity point of f. This is also the case if p∉A (since f(p) is not defined).
If (1) holds for each p in a set B⊆A, we say that f is continuous on B. If this is the case for B=A, we simply say that f is continuous.
Sometimes we prefer to keep x near p but different from p. We then replace Gp(δ) in (1) by the set Gp(δ)−{p}, i.e., the globe without its center, denoted G¬p(δ) and called the deleted δ -globe about p. This is even necessary if p∉Df. Replacing f(p) in (1) by some q∈T, we then are led to the following definition.
Given f:A→(T,ρ′),A⊆(S,ρ),p∈S, and q∈T, we say that f(x) tends to q as x tends to p(f(x)→q as x→p) iff for each ε>0 there is δ>0 such that ρ′(f(x),q)<ε for all x∈A∩G¬p(δ). In symbols,
(∀ε>0)(∃δ>0)(∀x∈A∩G¬p(δ)){ρ′(f(x),q)<ε, i.e. f(x)∈Gq(ε)
This means that f(x) is ε -close to q when x is δ -close to p and x≠p.
If (2) holds for some q, we call q a limit of f at p. There may be no such q. We then say that f has no limit at p, or that this limit does not exist. If there is only one such q( for a given p), we write q=limx→pf(x).
Note 1. Formula (2) holds "vacuously" (see Chapter 1,8 §§1-3, end remark) if A∩G¬p(δ)=∅ for some δ>0. Then any q∈T is a limit at p, so a limit exists but is not unique. (We discard the case where T is a singleton.)
Note 2. However, uniqueness is ensured if A∩G¬p(δ)≠∅ for all δ>0, as we prove below.
Observe that by Corollary 6 of Chapter 3, §14, the set A clusters at p iff
(∀δ>0)A∩G¬p(δ)≠∅.( Explain! )
Thus we have the following corollary.
If A clusters at p in (S,ρ), then a function f:A→(T,p′) can have at most one limit at p; i.e.
limx→pf(x) is unique (if it exists).
In particular, this holds if A⊇(a,b)⊂E1(a<b) and p∈[a,b].
- Proof
-
Suppose f has two limits, q and r, at p. By the Hausdorff property,
Gq(ε)∩Gr(ε)=∅ for some ε>0.
Also, by (2), there are δ′,δ′′>0 such that
(∀x∈A∩G¬p(δ′))f(x)∈Gq(ε) and (∀x∈A∩G¬p(δ′′))f(x)∈Gr(ε)
Let δ=min(δ′,δ′′). Then for x∈A∩G¬p(δ),f(x) is in both Gq(ε) and Gr(ε), and such an x exists since A∩G¬p(δ)≠∅ by assumption.
But this is impossible since Gq(ε)∩Gr(ε)=∅ ( a contradiction!). ◻
For intervals, see Chapter 3, §14, Example ( h).
f is continuous at p(p∈Df) iff f(x)→f(p) as x→p.
- Proof
-
The straightforward proof from definitions is left to the reader.
Note 3. In formula (2), we excluded the case x=p by assuming that x∈A∩G¬p(δ). This makes the behavior of f at p itself irrelevant. Thus for the existence of a limit q at p, it does not matter whether p∈Df or whether f(p)=q. But both conditions are required for continuity at p (see Corollary 2 and Definition 1).
Note 4. Observe that if (1) or (2) holds for some δ, it certainly holds for any δ′≤δ. Thus we may always choose δ as small as we like. Moreover, as x is limited to Gp(δ), we may disregard, or change at will, the function values f(x) for x∉Gp(δ) ("local character of the limit notion").
II. Limits in E*. If S or T is E∗( or E1), we may let x→±∞ or f(x)→±∞. For a precise definition, we rewrite (2) in terms of globes Gp and Gq:
(∀Gq)(∃Gp)(∀x∈A∩G¬p)f(x)∈Gq.
This makes sense also if p=±∞ or q=±∞. We only have to use our conventions as to G±∞, or the metric ρ′ for E∗, as explained in Chapter 3, §11.
For example, consider
′′f(x)→q as x→+∞′′(A⊆S=E∗,p=+∞,q∈(T,ρ′)).
Here Gp has the form (a,+∞],a∈E1, and G¬p=(a,+∞), while Gq=Gq(ε), as usual. Noting that x∈G¬p means x>a(x∈E1), we can rewrite (2′) as
(∀ε>0)(∃a∈E1)(∀x∈A|x>a)f(x)∈Gq(ε), or ρ′(f(x),q)<ε.
This means that f(x) becomes arbitrarily close to q for large x(x>a).
Next consider 4f(x)→+∞ as x→−∞ " Here G¬p=(−∞,a) and Gq=(b,+∞]. Thus formula (2′) yields (with S=T=E∗, and x varying over Ei)
(∀b∈E1)(∃a∈E1)(∀x∈A|x<a)f(x)>b;
similarly in other cases, which we leave to the reader.
Note 5. In (3), we may take A=N (the naturals). Then f:N→(T,ρ′) is a sequence in T. Writing m for x, set um=f(m) and a=k∈N to obtain
(∀ε>0)(∃k)(∀m>k)um∈Gq(ε); i.e., ρ′(um,q)<ε.
This coincides with our definition of the limit q of a sequence {um} (see Chapter 3, §14). Thus limits of sequences are a special case of function limits. Theorems on sequences can be obtained from those on functions f:A→(T,ρ′) by simply taking A=N and S=E∗ as above.
Note 6. Formulas (3) and (4) make sense sense also if S=E1 (respectively, S=T=E1) since they do not involve any mention of ±∞. We shall use such formulas also for functions f:A→T, with A⊆S⊆E1 or T⊆E1, as the case may be.
III. Relative Limits and Continuity. Sometimes the desired result (1) or (2) does not hold in full, but only with A replaced by a smaller set B⊆A. Thus we may have
(∀ε>0)(∃δ>0)(∀x∈B∩G¬p(δ))f(x)∈Gq(ε).
In this case, we call q a relative limit of f at p over B and write
"f(x)→q as x→p over B"
or
limx→p,x∈Bf(x)=q( if q is unique );
B is called the path over which x tends to p. If, in addition, p∈Df and q=f(p), we say that f is relatively continuous at p over B; then (1) holds with A replaced by B. Again, if this holds for every p∈B, we say that f is relatively continuous on B. Clearly, if B=A=Df, this yields ordinary (nonrelative) limits and continuity. Thus relative limits and continuity are more general.
Note that for limits over a path B,x is chosen from B or B−{p} only. Thus the behavior of f outside B becomes irrelevant, and so we may arbitrarily redefine f on −B. For example, if p∉B but limx→p,x∈Bf(x)=q exists, we may define f(p)=q, thus making f relatively continuous at p( over B). We also may replace (S,ρ) by (B,ρ)( if p∈B), or restrict f to B, i.e., replace f by the function g:B→(T,ρ′) defined by g(x)=f(x) for x∈B (briefly, g=f on B).
A particularly important case is
A⊆S⊆E∗, e.g., S=E1.
Then inequalities are defined in S, so we may take
B={x∈A|x<p} (points in A, preceding p).
Then, writing Gq for Gq(ε) and a=p−δ, we obtain from formula (2)
(∀Gq)(∃a<p)(∀x∈A|a<x<p)f(x)∈Gq.
If (5) holds, we call q a left limit of f at p and write
"f(x)→q as x→p−"("x tends to p from the left′).
If, in addition, q=f(p), we say that f is left continuous at p. Similarly, taking
B={x∈A|x>p},
we obtain right limits and continuity. We write
f(x)→q as x→p+
iff q is a right limit of f at p, i.e., if (5) holds with all inequalities reversed.
If the set B in question clusters at p, the relative limit (if any) is unique. We then denote the left and right limit, respectively, by f(p−) and f(p+), and we write
limx→p−f(x)=f(p−) and limx→p+f(x)=f(p+).
With the previous notation, if f(x)→q as x→p over a path B, and also over D, then f(x)→q as x→p over B∪D.
Hence if Df⊆E∗ and p∈E∗, we have
q=limx→pf(x) iff q=f(p−)=f(p+).( Exercise! )
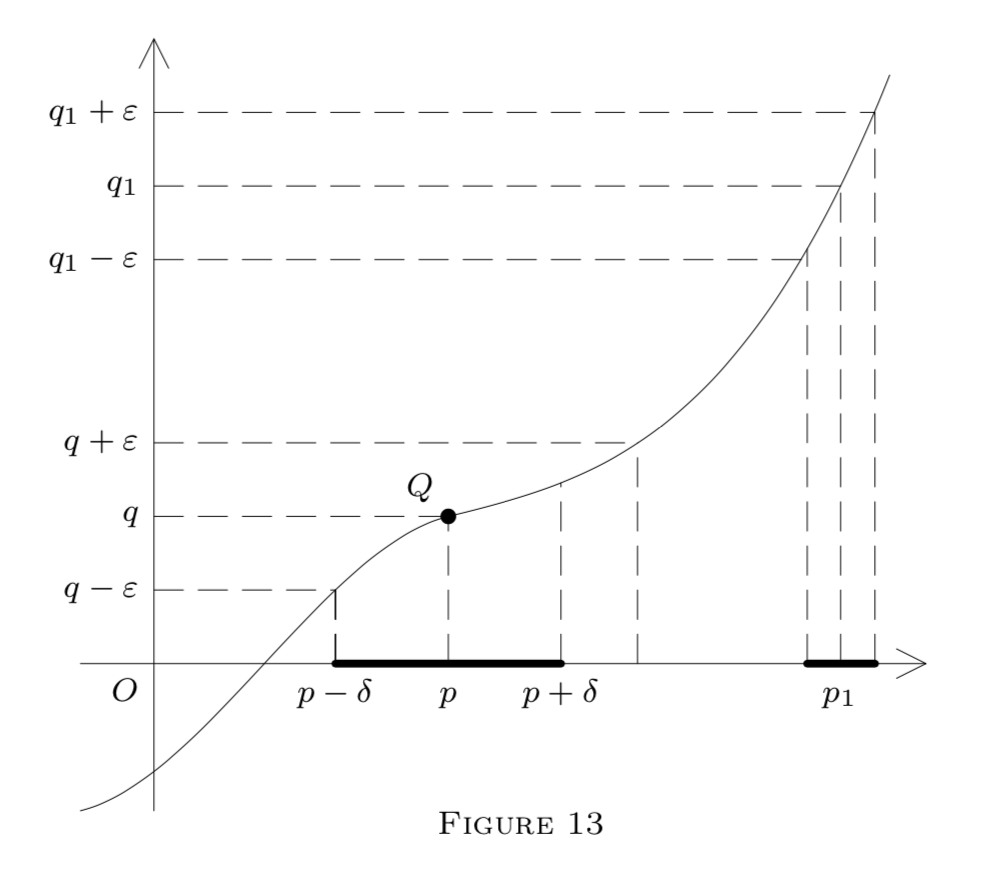
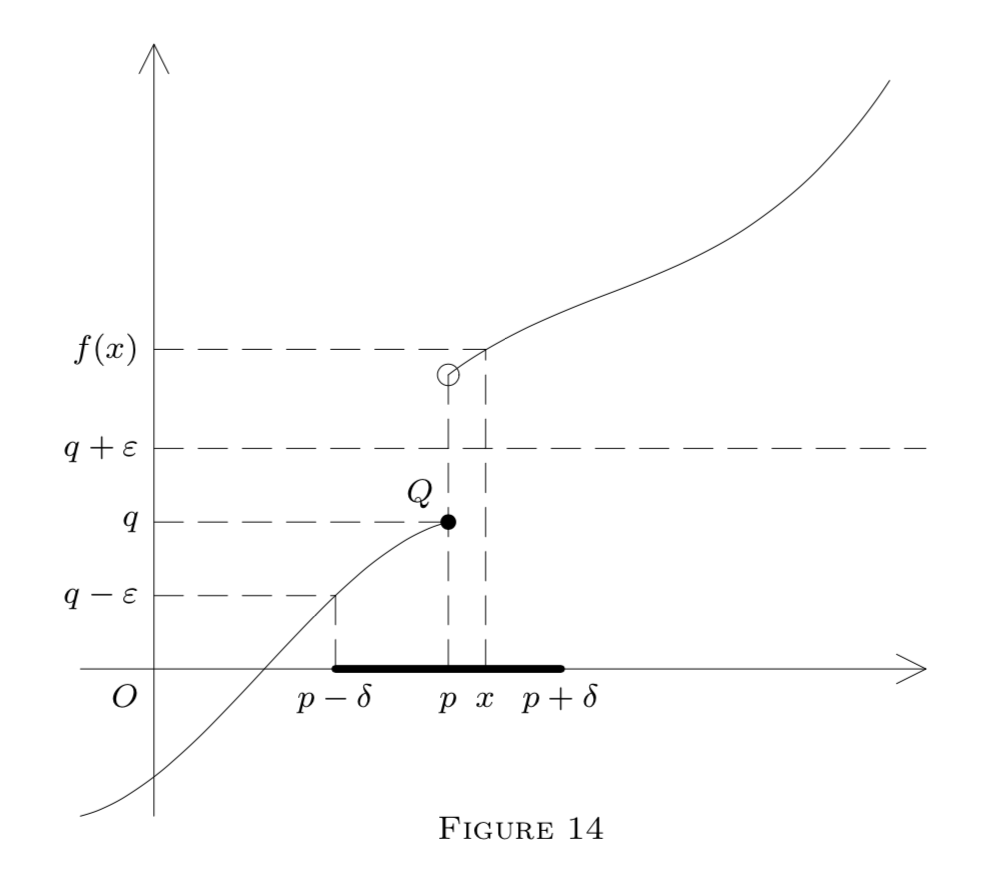
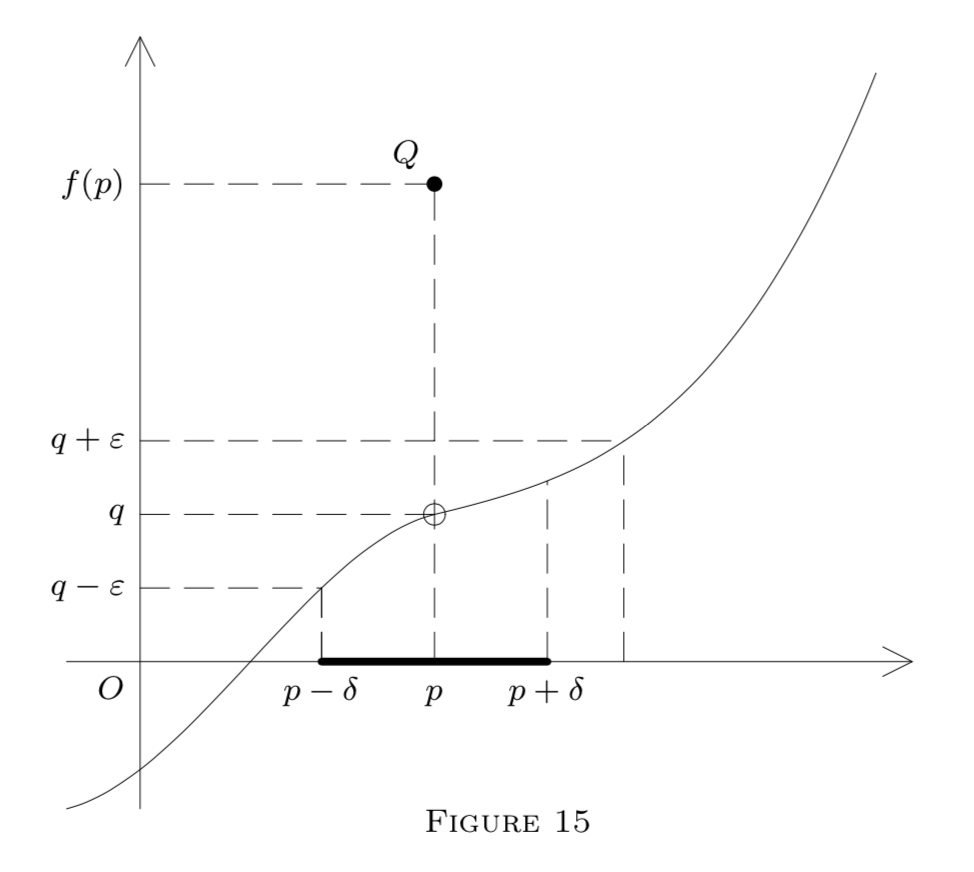
We now illustrate our definitions by a diagram in E2 representing a function f:E1→E1 by its graph, i.e., points (x,y) such that y=f(x).
Here
Gq(ε)=(q−ε,q+ε)
is an interval on the y -axis. The dotted lines show how to construct an interval
(p−δ,p+δ)=Gp
on the x -axis, satisfying formula (1) in Figure 13, formulas (5) and (6) in Figure 14, or formula (2) in Figure 15. The point Q in each diagram belongs to the graph; i.e., Q=(p,f(p)). In Figure 13,f is continuous at p( and also at p1 ). However, it is only left-continuous at p in Figure 14, and it is discontinuous at p in Figure 15, though f(p−) and f(p+) exist. (Why?)
(a) Let f:A→T be constant on B⊆A; i.e.
f(x)=q for a fixed q∈T and all x∈B.
Then f is relatively continuous on B, and f(x)→q as x \rightarrow p over B, at each p . (Given \varepsilon>0, take an arbitrary \delta>0. Then
\left(\forall x \in B \cap G_{\neg p}(\delta)\right) \quad f(x)=q \in G_{q}(\varepsilon),
as required; similarly for continuity.)
(b) Let f be the i dentity map on A \subset(S, \rho) ; i.e.,
(\forall x \in A) \quad f(x)=x.
Then, given \varepsilon>0, take \delta=\varepsilon to obtain, for p \in A,
\left(\forall x \in A \cap G_{p}(\delta)\right) \quad \rho(f(x), f(p))=\rho(x, p)<\delta=\varepsilon.
Thus by (1), f is continuous at any p \in A, hence on A.
(c) Define f : E^{1} \rightarrow E^{1} by
f(x)=1 \text{ if } x \text{ is rational, and } f(x)=0 \text{ otherwise.}
(This is the Dirichlet function, so named after Johann Peter Gustav Lejeune Dirichlet.)
No matter how small \delta is, the globe
G_{p}(\delta)=(p-\delta, p+\delta)
(even the deleted globe) contains both rationals and irrationals. Thus as x varies over G_{\neg p}(\delta), f(x) takes on both values, 0 and 1, many times and so gets out of any G_{q}(\varepsilon), with q \in E^{1}, \varepsilon<\frac{1}{2}.
Hence for any q, p \in E^{1}, formula (2) fails if we take \varepsilon=\frac{1}{4}, say. Thus f has no limit at any p \in E^{1} and hence is discontinuous everywhere! However, f is relatively continuous on the set R of all rationals by Example (\mathrm{a}).
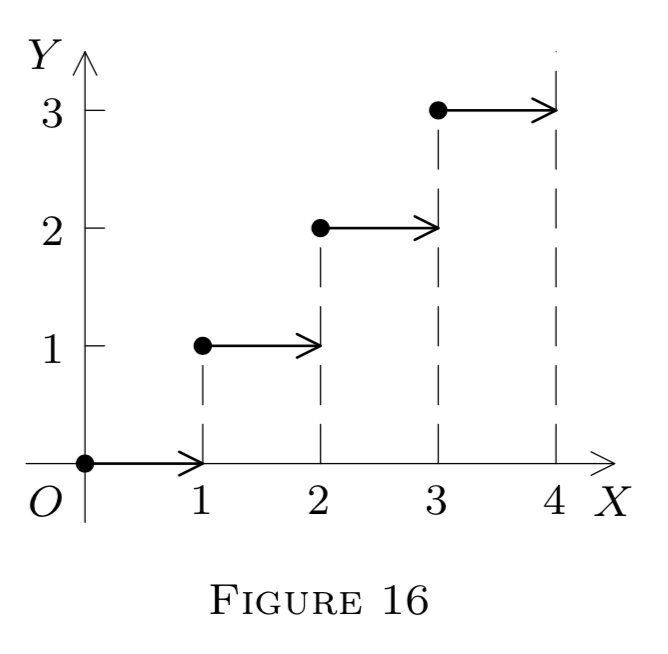
(d) Define f : E^{1} \rightarrow E^{1} by
f(x)=[x](=\text { the integral part of } x ; \text { see Chapter } 2, §10).
Thus f(x)=0 for x \in[0,1), f(x)=1 for x \in[1,2), etc. Then f is discontinuous at p if p is an integer (why?) but continuous at any other p\left(\text { restrict } f \text { to a small } G_{p}(\delta) \text { so as to make it constant) }\right.
However, left and right limits exist at each p \in E^{1}, even if p= n(\text { an integer }) . In fact,
f(x)=n, x \in(n, n+1)
and
f(x)=n-1, x \in(n-1, n),
hence f\left(n^{+}\right)=n and f\left(n^{-}\right)= n-1 ; f is right continuous on E^{1} . See Figure 16 .
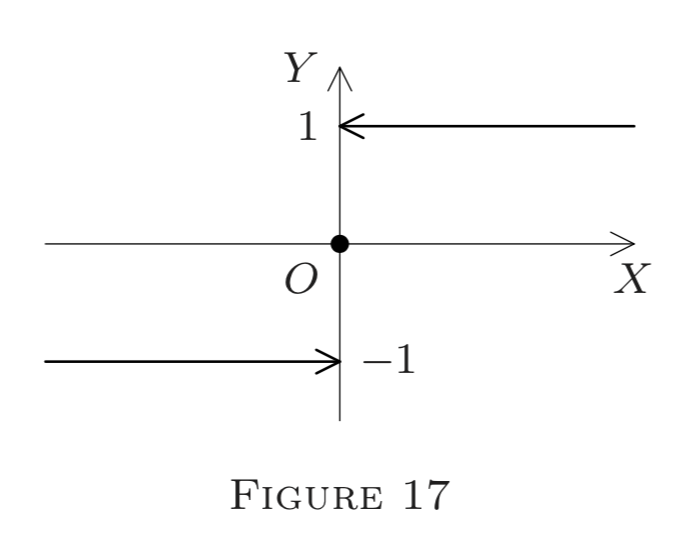
(e) Define f : E^{1} \rightarrow E^{1} by
f(x)=\frac{x}{|x|} \text{ if } x \neq 0, \text{ and } f(0)=0.
(This is the so-called signum function, often denoted by sgn.)
Then (Figure 17)
f(x)=-1 \text{ if } x<0
and
f(x)=1 \text{ if } x>0.
Thus, as in ( d ), we infer that f is discontinuous at 0, but continuous at each p \neq 0 . Also, f\left(0^{+}\right)=1 and f\left(0^{-}\right)=-1 . Redefining f(0)=1 or f(0)=-1, we can make f right (respectively, left) continuous at 0, but not both.
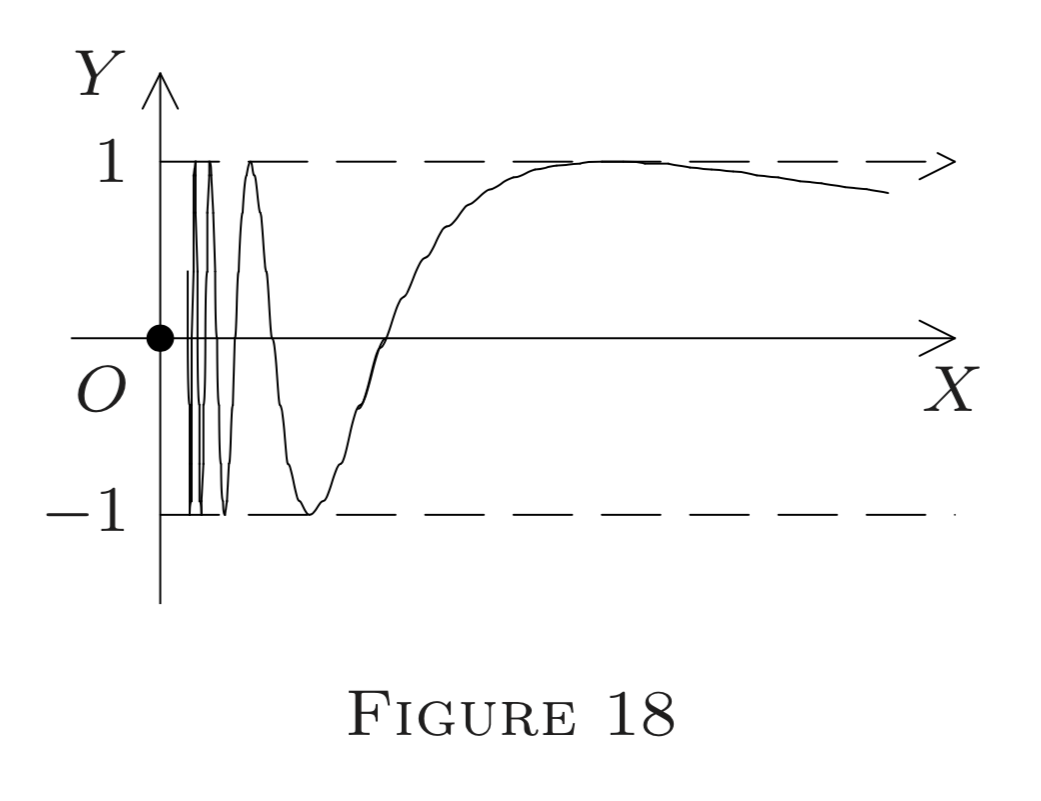
(f) Define f : E^{1} \rightarrow E^{1} by (see Figure 18)
f(x)=\sin \frac{1}{x} \text{ if } x \neq 0, \text{ and } f(0)=0.
Any globe G_{0}(\delta) about 0 contains points at which f(x)=1, as well as those at which f(x)=-1 or f(x)=0 (take x=2 /(n \pi) for large integers n ); in fact, the graph "oscillates" infinitely many times between -1 and 1 . Thus by the same argument as in (\mathrm{c}), f has no limit at 0 (not even a left or right limit) and hence is discontinuous at 0 . No attempt at redefining f at 0 can restore even left or right continuity, let alone ordinary continuity, at 0 .
(g) Define f : E^{2} \rightarrow E^{1} \mathrm{by}
f(\overline{0})=0 \text{ and } f(\overline{x})=\frac{x_{1} x_{2}}{x_{1}^{2}+x_{2}^{2}} \text{ if } \overline{x}=\left(x_{1}, x_{2}\right) \neq \overline{0}.
Let B be any line in E^{2} through \overline{0}, given parametrically by
\overline{x}=t \vec{u}, \quad t \in E^{1}, \vec{u} \text{ fixed (see Chapter 3, §§4-6 ),}
so x_{1}=t u_{1} and x_{2}=t u_{2} . As is easily seen, for \overline{x} \in B, f(\overline{x})=f(\overline{u}) (constant) if \overline{x} \neq \overline{0} . Hence
\left(\forall \overline{x} \in B \cap G_{\neg \overline{0}}(\delta)\right) \quad f(\overline{x})=f(\overline{u}),
i.e., \rho(f(\overline{x}), f(\overline{u}))=0<\varepsilon, for any \varepsilon>0 and any deleted globe about \overline{0}.
By \left(2^{\prime}\right), then, f(\overline{x}) \rightarrow f(\overline{u}) as \overline{x} \rightarrow \overline{0} over the path B . Thus f has a relative limit f(\overline{u}) at \overline{0}, over any line \overline{x}=t \overline{u}, but this limit is different for various choices of \overline{u}, i.e., for different lines through \overline{0} . No ordinary limit at \overline{0} exists (why?); f is not even relatively continuous at \overline{0} over the line \overline{x}=t \vec{u} unless f(\overline{u})=0 (which is the case only if the line is one of the coordinate axes (why?)).


