5.10: Sufficient Condition of Integrability. Regulated Functions
- Page ID
- 21246
This page is a draft and is under active development.
In this section, we shall determine a large family of functions that do have antiderivatives. First, we give a general definition, valid for any range space \((T, p)\) (not necessarily \(E).\) The domain space remains \(E^{1}\).
A function \(f : E^{1} \rightarrow(T, p)\) is said to be regulated on an interval \(I \subseteq E^{1},\) with endpoints \(a<b,\) iff the limits \(f\left(p^{-}\right)\) and \(f\left(p^{+}\right),\) other than \(\pm \infty,\) exist at each \(p \in I.\) However, at the endpoints \(a, b,\) if in \(I,\) we only require \(f\left(a^{+}\right)\) and \(f\left(b^{-}\right)\) to exist.
(a) If \(f\) is relatively continuous and finite on \(I,\) it is regulated.
(b) Every real monotone function is regulated (see Chapter 4, §5, Theorem 1).
(c) If \(f : E^{1} \rightarrow E^{n}\left(^{*} C^{n}\right)\) has bounded variation on \(I,\) it is regulated (§7, Theorem 4).
(d) The characteristic function of a set \(B,\) denoted \(C_{B},\) is defined by
\[C_{B}(x)=1 \text { if } x \in B \text { and } C_{B}=0 \text { on }-B.\]
For any interval \(J \subseteq E^{1}, C_{J}\) is regulated on \(E^{1}\).
(e) A function \(f\) is called a step function on \(I\) iff \(I\) can be represented as the union, \(I=\bigcup_{k} I_{k},\) of a sequence of disjoint intervals \(I_{k}\) such that \(f\) is constant and \(\neq \pm \infty\) on each \(I_{k}\). Note that some \(I_{k}\) may be singletons, \(\{p\}.\)
If the number of the \(I_{k}\) is finite, we call \(f\) a simple step function.
When the range space \(T\) is \(E,\) we can give the following convenient alternative definition. If, say, \(f=a_{k} \neq \pm \infty\) on \(I_{k},\) then
\[f=\sum_{k} a_{k} C_{I_{k}} \quad \text { on } I,\]
where \(C_{I_{k}}\) is as in (d). Note that \(\sum_{k} a_{k} C_{I_{k}}(x)\) always exists for disjoint \(I_{k}.\) (Why?)
Each simple step function is regulated. (Why?)
Let the functions \(f, g, h\) be real or complex (or let \(f, g\) be vector valued and h scalar valued).
If they are regulated on \(I,\) so are \(f \pm g, f h,\) and \(|f|;\) so also is \(f / h\) if \(h\) is bounded away from 0 on \(I,\) i.e., \((\exists \varepsilon>0)|h| \geq \varepsilon\) on \(I.\)
- Proof
-
The proof, based on the usual limit properties, is left to the reader.
We shall need two lemmas. One is the famous Heine-Borel lemma.
If a closed interval \(A=[a, b]\) in \(E^{1}\) (or \(E^{n})\) is covered by open sets \(G_{i}(i \in I),\) i.e.,
\[A \subseteq \bigcup_{i \in I} G_{i},\]
then \(A\) can be covered by a finite number of these \(G_{i}\).
- Proof
-
The proof was sketched in Problem 10 of Chapter 4, §6.
Note 1. This fails for nonclosed intervals \(A.\) For example, let
\[A=(0,1) \subseteq E^{1} \text { and } G_{n}=\left(\frac{1}{n}, 1\right).\]
Then
\[A=\bigcup_{n=1}^{\infty} G_{n}(\text { verify! }), \text { but not } A \subseteq \bigcup_{n=1}^{m} G_{n}\]
for any finite \(m.\) (Why?)
The lemma also fails for nonopen sets \(G_{i}.\) For example, cover \(A\) by singletons \(\{x\}, x \in A.\) Then none of the \(\{x\}\) can be dropped!
If a function \(f : E^{1} \rightarrow T\) is regulated on \(I=[a, b],\) then \(f\) can be uniformly approximated by simple step functions on \(I.\)
That is, for any \(\varepsilon>0,\) there is a simple step function \(g,\) with \(\rho(f, g) \leq \varepsilon\) on \(I;\) hence
\[\sup _{x \in I} \rho(f(x), g(x)) \leq \varepsilon.\]
- Proof
-
By assumption, \(f\left(p^{-}\right)\) exists for each \(p \in(a, b],\) and \(f\left(p^{+}\right)\) exists for \(p \in[a, b),\) all finite.
Thus, given \(\varepsilon>0\) and any \(p \in I,\) there is \(G_{p}(\delta\)) \((\delta\) depending on \(p\)) such that \(\rho(f(x), r)<\varepsilon\) whenever \(r=f\left(p^{-}\right)\) and \(x \in(p-\delta, p),\) and \(\rho(f(x), s)<\varepsilon\) whenever \(s=f\left(p^{+}\right)\) and \(x \in(p, p+\delta); x \in I\)
We choose such a \(G_{p}(\delta)\) for every \(p \in I.\) Then the open globes \(G_{p}=G_{p}(\delta)\) cover the closed interval \(I=[a, b],\) so by Lemma 1, \(I\) is covered by a finite number of such globes, say,
\[I \subseteq \bigcup_{k=1}^{n} G_{p_{k}}\left(\delta_{k}\right), \quad a \in G_{p_{1}}, a \leq p_{1}<p_{2}<\cdots<p_{n} \leq b.\]
We now define the step function \(g\) on \(I\) as follows.
If \(x=p_{k},\) we put
\[g(x)=f\left(p_{k}\right), \quad k=1,2, \ldots, \text{ } n.\]
If \(x \in\left[a, p_{1}\right),\) then
\[g(x)=f\left(p_{1}^{-}\right).\]
If \(x \in\left(p_{1}, p_{1}+\delta_{1}\right),\) then
\[g(x)=f\left(p_{1}^{+}\right).\]
More generally, if \(x\) is in \(G_{\neg p_{k}}\left(\delta_{k}\right)\) but in none of the \(G_{p_{i}}\left(\delta_{i}\right), i<k,\) we put
\[g(x)=f\left(p_{k}^{-}\right) \quad \text { if } x<p_{k}\]
and
\[g(x)=f\left(p_{k}^{+}\right) \quad \text { if } x>p_{k}.\]
Then by construction, \(\rho(f, g)<\varepsilon\) on each \(G_{p_{k}},\) hence on \(I. \quad \square\)
*Note 2. If \(T\) is complete, we can say more: \(f\) is regulated on \(I=[a, b]\) iff \(f\) is uniformly approximated by simple step functions on \(I\). (See Problem 2.)
If \(f : E^{1} \rightarrow E\) is regulated on an interval \(I \subseteq E^{1}\) and if \(E\) is complete, then \(\int f\) exists on \(I,\) exact at every continuity point of \(f\) in \(I^{0}\).
In particular, all continuous maps \(f : E^{1} \rightarrow E^{n}\left(^{*} C^{n}\right)\) have exact primitives.
- Proof
-
In view of Problem 14 of §5, it suffices to consider closed intervals.
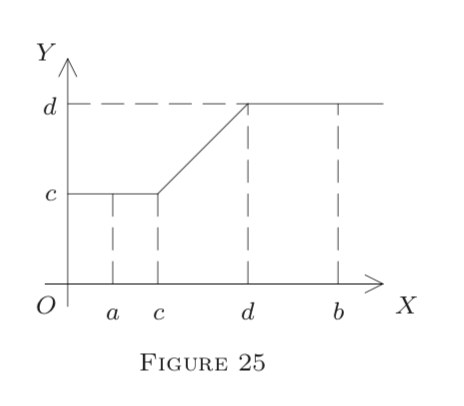
Thus let \(I=[a, b], a<b,\) in \(E^{1}.\) Suppose first that \(f\) is the characteristic function \(C_{J}\) of a subinterval \(J \subseteq I\) with endpoints \(c\) and \(d\) \((a \leq c \leq d \leq b),\) so \(f=1\) on \(J\) and \(f=0\) on \(I-J.\) We then define \(F(x)=x\) on \(J, F=c\) on \([a, c],\) and \(F=d\) on \([d, b]\) (see Figure 25). Thus \(F\) is continuous (why?), and \(F^{\prime}=f\) on \(I-\{a, b, c, d\}\) (why?). Hence \(F=\int f\) on \(I;\) i.e., characteristic functions are integrable.
Then, however, so is any simple step function
\[f=\sum_{k=1}^{m} a_{k} C_{I_{k}},\]
by repeated use of Corollary 1 in §5.
Finally, let \(f\) be any regulated function on \(I\). Then by Lemma 2, for any \(\varepsilon_{n}=\frac{1}{n},\) there is a simple step function \(g_{n}\) such that
\[\sup _{x \in I}\left|g_{n}(x)-f(x)\right| \leq \frac{1}{n}, \quad n=1,2, \ldots.\]
As \(\frac{1}{n} \rightarrow 0,\) this implies that \(g_{n} \rightarrow f\) (uniformly) on \(I\) (see Chapter 4, §12, Theorem 1). Also, by what was proved above, the step functions \(g_{n}\) have antiderivatives, hence so has \(f\) (Theorem 2 in §9); ; i.e., \(F=\int f\) exists on \(I,\) as claimed. Moreover, \(\int f\) is exact at continuity points of \(f\) in \(I^{0}\) (Problem 10 in §5). \(\quad \square\)
In view of the sufficient condition expressed in Theorem 2, we can now replace the assumption "\(\int f\) exists" in our previous theorems by "\(f\) is regulated" (provided \(E\) is complete). For example, let us now review Problems 7 and 8 in §5.
Let \(f : E^{1} \rightarrow E\) (\(E\) complete) and \(g : E^{1} \rightarrow E^{1}\) be regulated on \(I=[a, b],\) with \(g \geq 0\) on \(I.\) Then the following are true:
(i) There is a finite \(c \in E\) (called the "g-weighted mean of \(f\) on \(I\)") such that \(\int_{a}^{b} g f=c \int_{a}^{b} g\).
(ii) If \(f,\) too, is real and has the Darboux property on \(I,\) then \(c=f(q)\) for some \(q \in I.\)
- Proof
-
Indeed, as \(f\) and \(g\) are regulated, so is \(g f\) by Theorem 1. Hence by Theorem 2, \(\int f\) and \(\int g f\) exist on \(I.\) The rest follows as in Problems 7 and 8 of §5. \(\quad \square\)
Suppose \(f\) and \(g\) are real, \(f\) is monotone with \(f=\int f^{\prime}\) on \(I,\) and \(g\) is regulated on \(I; I=[a, b].\) Then
\[\int_{a}^{b} f g=f(a) \int_{a}^{q} g+f(b) \int_{q}^{b} g \text { for some } q \in I.\]
- Proof
-
To fix ideas, let \(f \uparrow;\) i.e., \(f^{\prime} \geq 0\) on \(I\).
The formula \(f=\int f^{\prime}\) means that \(f\) is relatively continuous (hence regulated) on \(I\) and differentiable on \(I-Q\) (\(Q\) countable). As \(g\) is regulated,
\[\int_{a}^{x} g=G(x)\]
does exist on \(I,\) so \(G\) has similar properties, with \(G(a)=\int_{a}^{a} g=0\).
By Theorems 1 and 2, \(\int f G^{\prime}=\int f g\) exists on \(I.\) (Why?) Hence by Corollary 5 in §5, so does \(\int G f^{\prime},\) and we have
\[\int_{a}^{b} f g=\int_{a}^{b} f G^{\prime}=f(x) G\left.(x)\right|_{a} ^{b}-\int_{a}^{b} G f^{\prime}=f(b) G(b)-\int_{a}^{b} G f^{\prime}.\]
Now \(G\) has the Darboux property on \(I\) (being relatively continuous), and \(f^{\prime} \geq 0.\) Also, \(\int G\) and \(\int G f^{\prime}\) exist on \(I.\) Thus by Problems 7 and 8 in §5,
\[\int_{a}^{b} G f^{\prime}=G(q) \int_{a}^{b} f^{\prime}=G(q) f\left.(x)\right|_{a} ^{b}, \quad q \in I.\]
Combining all, we obtain the required result (1) since
\[\begin{aligned} \int f g &=f(b) G(b)-\int_{a}^{b} G f^{\prime} \\ &=f(b) G(b)-f(b) G(q)+f(a) G(q) \\ &=f(b) \int_{q}^{b} g+f(a) \int_{a}^{q} g . \quad \square \end{aligned}\]
We conclude with an application to infinite series. Given \(f : E^{1} \rightarrow E,\) we define
\[\int_{a}^{\infty} f=\lim _{x \rightarrow+\infty} \int_{a}^{x} f \text { and } \int_{-\infty}^{a} f=\lim _{x \rightarrow-\infty} \int_{x}^{a} f\]
if these integrals and limits exist.
We say that \(\int_{a}^{\infty} f\) and \(\int_{-\infty}^{a} f\) converge iff they exist and are finite.
If \(f : E^{1} \rightarrow E^{1}\) is nonnegative and nonincreasing on \(I=[a,+\infty),\) then
\[\int_{a}^{\infty} f \text { converges iff } \sum_{n=1}^{\infty} f(n) \text { does.}\]
- Proof
-
As \(f \downarrow, f\) is regulated, so \(\int f\) exists on \(I=[a,+\infty).\) We fix some natural \(k \geq a\) and define
\[F(x)=\int_{k}^{x} f \text { for } x \in I.\]
By Theorem 3(iii) in §5, \(F \uparrow\) on \(I\). Thus by monotonicity,
\[\lim _{x \rightarrow+\infty} F(x)=\lim _{x \rightarrow+\infty} \int_{k}^{x} f=\int_{k}^{\infty} f\]
exists in \(E^{*};\) so does \(\int_{a}^{k} f.\) Since
\[\int_{a}^{x} f=\int_{a}^{k} f+\int_{k}^{x} f,\]
where \(\int_{a}^{k} f\) is finite by definition, we have
\[\int_{a}^{\infty} f<+\infty \text { iff } \int_{k}^{\infty} f<+\infty.\]
Similarly,
\[\sum_{n=1}^{\infty} f(n)<+\infty \quad \text { iff } \sum_{n=k}^{\infty} f(n)<+\infty.\]
Thus we may replace "\(a\)" by "\(k\)."
Let
\[I_{n}=[n, n+1), \quad n=k, k+1, \ldots,\]
and define two step functions, \(g\) and \(h,\) constant on each \(I_{n},\) by
\[h=f(n) \text { and } g=f(n+1) \text { on } I_{n}, n \geq k.\]
Since \(f \downarrow,\) we have \(g \leq f \leq h\) on all \(I_{n},\) hence on \(J=[k,+\infty).\) Therefore,
\[\int_{k}^{x} g \leq \int_{k}^{x} f \leq \int_{k}^{x} h \text { for } x \in J.\]
Also,
\[\int_{k}^{m} h=\sum_{n=k}^{m-1} \int_{n}^{n+1} h=\sum_{n=k}^{m-1} f(n),\]
since \(h=f(n)\) (constant) on \([n, n+1),\) and so
\[\int_{n}^{n+1} h(x) d x=f(n) \int_{n}^{n+1} 1 d x=f(n) \cdot\left.x\right|_{n} ^{n+1}=f(n)(n+1-n)=f(n).\]
Similarly,
\[\int_{k}^{m} g=\sum_{n=k}^{m-1} f(n+1)=\sum_{n=k+1}^{m} f(n).\]
Thus we obtain
\[\sum_{n=k+1}^{m} f(n)=\int_{k}^{m} g \leq \int_{k}^{m} f \leq \int_{k}^{m} h=\sum_{n=k}^{m-1} f(n),\]
or, letting \(m \rightarrow \infty\),
\[\sum_{n=k+1}^{\infty} f(n) \leq \int_{k}^{\infty} f \leq \sum_{n=k}^{\infty} f(n).\]
Hence \(\int_{k}^{\infty} f\) is finite iff \(\sum_{n=1}^{\infty} f(n)\) is, and all is proved. \(\quad \square\)
(f) Consider the hyperharmonic series
\[\sum \frac{1}{n^{p}} \quad \text {(Problem 2 of Chapter 4, §13).}\]
Let
\[f(x)=\frac{1}{x^{p}}, \quad x \geq 1.\]
If \(p=1,\) then \(f(x)=1 / x,\) so \(\int_{1}^{x} f=\ln x \rightarrow+\infty\) as \(x \rightarrow+\infty.\) Hence \(\sum 1 / n\) diverges.
If \(p \neq 1,\) then
\[\int_{1}^{\infty} f=\lim _{x \rightarrow+\infty} \int_{1}^{x} f=\lim _{x \rightarrow+\infty}\left.\frac{x^{1-p}}{1-p}\right|_{1} ^{x},\]
so \(\int_{1}^{\infty} f\) converges or diverges according as \(p>1\) or \(p<1,\) and the same applies to the series \(\sum 1 / n^{p}.\)
(g) Even nonregulated functions may be integrable. Such is Dirichlet's function (Example (c) in Chapter 4, §1). Explain, using the countability of the rationals.