3.2: The Transformation w=1/z

 

 

Consider the equation

\(w=\frac{1}{z}\)

which establishes a one-to-one correspondence between the nonzero points of the \(z\) and \(w\) planes. Since \(z\bar{z}=\left | z \right |^{2}\), the mapping can be described by means of the successive transformations

\(g\left ( z \right )=\frac{z}{\left | z \right |^{2}}\).

The first transformation \(g(z)\) is an inversion with respect to the unit circle \(\left | z \right |=1\). That is, the image of a nonzero point \(z\) is the point \(g(z)\) with the properties

\(\left | g\left ( z \right ) \right |=\frac{1}{\left | z \right |}\)    and    \(arg\,g(z)=arg\, z\).

Thus the points exterior to the circle \(\left | z \right |=1\) are mapped onto the nonzero points interior to it, and conversely. Any point on the circle is mapped onto itself. The second transformation \(f\left ( z \right )=\overline{g\left ( z \right )}\) is simply a reflection in the real axis.

If we consider the function

\(T\left ( z \right )=\frac{1}{z}\)    ,    \(z\neq 0\)

we can define \(T\) at the origin and at the point at infinity so as to be continuous on the extended complex plane. In order to make \(T\) continuous on the extended plane, then, we write

\(T(0)=∞\),    \(T(∞)=0\),    and    \(T\left ( z \right )=\frac{1}{z}\)

for the remaining values of \(z\).

---

Mappings by \(1/z\)

An interesting property of the mapping \(w=1/z\) is that it transforms circles and lines into circles and lines.

You can observe this intuitively in the following applet. Things to try:

• Select between a Line or Circle.
• Drag points around on the left-side window. You can also change the position of the line or circle by dragging the grey points.

INTERACTIVE GRAPH

 

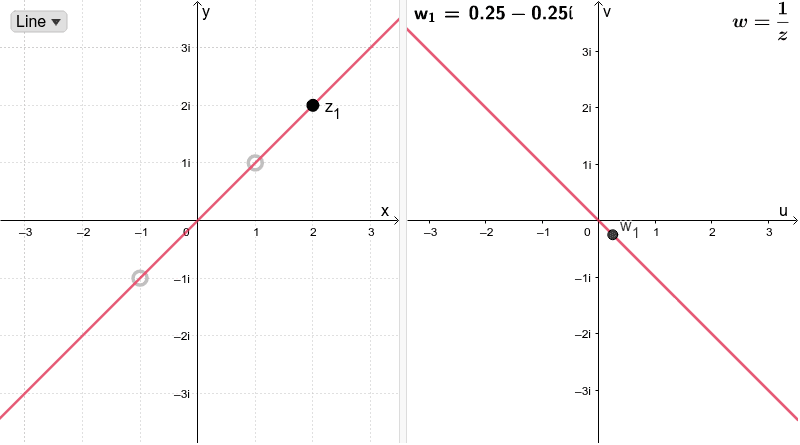
Observe carefully what happens to the points \(w_{1}\),\(w_{2}\) (the image of \(z_{1}\) and \(z_{2}\), respectively) on the \(uv\)-plane, shown on the right-side window.

• What do you notice when the line on the \(xy\)-plane crosses the origin?
• What happens when the circle on the \(xy\)-plane crosses the origin?

 

When \(A\), \(B\), \(C\) and \(D\) are all real numbers satisfying the condition \(B^{2}+C^{2}> 4AD\), the equation

\(A\left ( x^{2}+y^{2} \right )+Bx+Cx+D=0\)    (1)

represents an arbitrary circle or line, where \(A≠0\) for a circle and \(A=0\) for a line.

By using the method of completing the squares, we can rewrite equation (1) as follows

\(\left ( x+\frac{B}{2A} \right )^{2}+\left ( y+\frac{C}{2A} \right )^{2}=\left ( \frac{\sqrt{B^{2}+C^{2}-4AD}}{2A} \right )^{2}\)

This makes evident the need for condition \(B^{2}+C^{2}>4AD\) when \(A≠0\). When \(A=0\), the condition becomes \(B^{2}+C^{2}>0\), which means that \(B\) and \(C\) are not both zero.

Now, using the relations

\(x=\frac{z+\bar{z}}{2}\),    \(x=\frac{z-\bar{z}}{2i}\)    (2)

we can rewrite equation (1) in the form

\(2Az\bar{z}+\left ( B-iC \right )+(B+iC)\bar{z}+2D=0\).    (3)

Since \(w=1/z\), equation (3) becomes

\(2Dw\bar{w}+\left ( B+iC \right )w+(B-iC)\bar{w}+2A=0\)

and using the relations

\(u=\frac{w+\bar{w}}{2}\),    \(v=\frac{w-\bar{w}}{2i}\),    (4)

we obtain

\(D\left ( u^{2}+v^{2} \right )+Bu-Cv+A=0\)    (5)

which also represents a circle or line.

It is now clear from equations (1) and (5) that

1. a circle (\(A≠0)\) not passing through the origin \((D≠0)\) in the \(z\) plane is transformed into a circle not passing through the origin in the \w(\) plane;
2. a circle (\(A≠0)\)A≠0 through the origin \((D=0)\) in the \(z\) plane is transformed into a line that does not pass through the origin in the \(w\) plane;
3. a line (\(A=0)\) not passing through the origin \((D≠0)\) in the \(z\) plane is transformed into a circle through the origin in the \(w\) plane;
4. a line (\(A=0)\) through the origin \((D=0)\) in the \(z\) plane is transformed into a line through the origin in the \(w\) plane.

Exercise \(\PageIndex{1}\)

Verify that the expression \(D\left ( u^{2}+v^{2} \right )+Bu-Cv+A=0\) can be obtained from (1) using the relations (2) and (4).