4.1: Curves in the Complex Plane

Suppose the continuous real-valued functions \(x=x(t)\), \(y=y(t)\), \(a≤t≤\)b, are parametric equations of a curve \(C\) in the complex plane. If we use these equations as the real and imaginary parts in \(z=x+iy\), we can describe the points \(z\) on \(C\) by means of a complex-valued function of a real variable \(t\) called a parametrization of \(C\):

\(z(t)=x(t)+iy(t)\),    \(a≤t≤b\).    (1)

The point \(z(a)=x(a)+iy(a)\) or \(z_{0}=\left ( x\left ( a \right ),y\left ( a \right ) \right )\) is called the initial point of \(C\) and \(z(b)=x(b)+iy(b)\) or \(z_{1}=\left ( x\left ( b \right ) ,y\left ( b \right )\right )\) is its terminal point. The expression \(z(t)=x(t)+iy(t)\) could also be interpreted as a two-dimensional vector function. Consequently, \(z(a)\) and \(z(b)\) can be interpreted as position vectors. As tt varies from \(t=a\) to \(t=b\) we can envision the curve \(C\) being traced out by the moving arrowhead of \(z(t)\). This can be appreciated in the following applet with \(0≤t≤1\).

PressStartto animate. You can move the points to change the curve.

For example, the parametric equations \(x=cos\,⁡t\), \(y=sin⁡\,t\), \(0\leq t\leq 2\pi \), describe a unit circle centered at the origin. A parametrization of this circle is \(z(t)=cos\,⁡t+i\,sin⁡\,t\), or \(z\left ( t \right )=e^{it}\), \(0\leq t\leq 2\pi \).

PressStartto animate.

---

Contours

The notions of curves in the complex plane that are smooth, piecewise smooth, simple, closed, and simple closed are easily formulated in terms of the vector function (1). Suppose the derivative of (1) is \(z′(t)=x′(t)+iy′(t)\). We say a curve \(C\) in the complex plane is smooth if \(z′(t)\) is continuous and never zero in the interval \(a≤t≤b\). As shown in Figure 2, since the vector z′(t)\(\) is not zero at any point \(P\) on \(C\), the vector \(z′(t)\) is tangent to \(C\) at \(P\). Thus, a smooth curve has a continuously turning tangent; or in other words, a smooth curve can have no sharp corners or cusps. See Figure 2.

Figure 1: \(z′(t)=x′(t)+iy(t)\) as a tangent vector.

Figure 2: Curve \(C\) is not smooth since it has a cusp.

A piecewise smooth curve \(C\) has a continuously turning tangent, except possibly at the points where the component smooth curves \(C_{1},C_{2},\cdots ,C_{n}\) are joined together.

Figure 3: A piecewise smooth curve.

A curve \(C\) in the complex plane is said to be a simple if \(z\left ( t_{1} \right )\neq z\left ( t_{2} \right )\) for \(t_{1}\neq t_{2}\), except possibly for \(t=a\) and \(t=b\). \(C\) is a closed curve if \(z(a)=z(b)\).

Figure 4: Simple curve.

Figure 5: Non simple curve.

\(C\) is a simple closed curve if \(z\left ( t_{1} \right )\neq z\left ( t_{2} \right )\) for \(t_{1}≠t_{2}\) and \(z(a)=z(b)\).

Figure 4: Simple closed curve.

Figure 5: Non simple closed curve.

In complex analysis, a piecewise smooth curve \(C\) is called a contour or path. We define the positive direction on a contour \(C\) to be the direction on the curve corresponding to increasing values of the parameter \(t\). It is also said that the curve \(C\) has positive orientation. In the case of a simple closed countour \(C\), the positive direction corresponds to the counter-clockwise direction. For example, the circle \(z\left ( t \right )=e^{it}\), \(0\leq t\leq 2\pi \), has positive orientation. The negative direction on a contour \(C\) is the direction opposite the positive direction. If \(C\) has an orientation, the opposite curve, that is, a curve with opposite orientation, is denoted by \(−C\). On a simple closed curve, the negative direction corresponds to the clockwise direction. For instance, the circle \(z\left ( t \right )=e^{-it}\), \(0\leq t\leq 2\pi \), has negative orientation.

Figure 6: Positively oriented.

Figure 7: Negatively oriented.

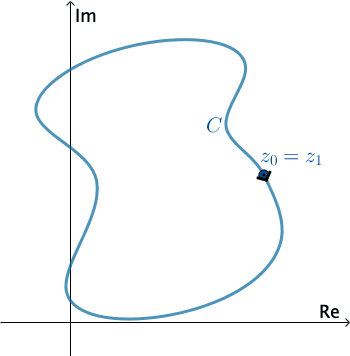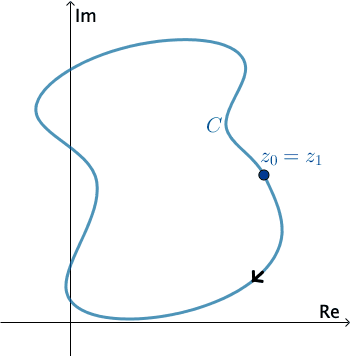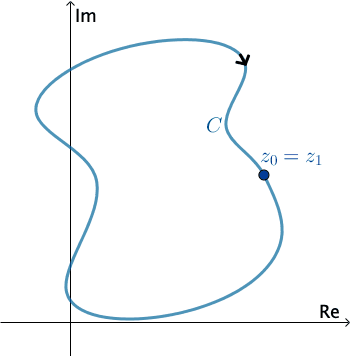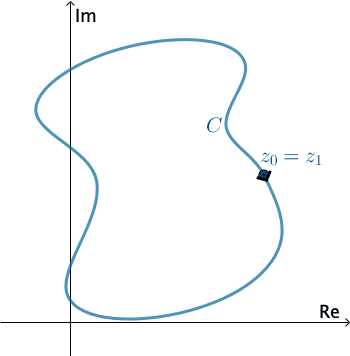
PressStartto animate. You can change the direction of  \(C\).

Exercise \(\PageIndex{1}\)

Exercise: There is no unique parametrization for a contour \(C\). You should verify that

\(z\left ( t \right )=e^{it}=cos\,t+i\,sin\,t\),\(0\leq t\leq 2\pi \)

\(z\left ( t \right )=e^{2\pi it}=cos\left (2\pi t\right )+i\,sin\left (2\pi  t \right )\),\(0\leq t\leq 1 \)

\(z\left ( t \right )=e^{\pi /2it}=cos\left (\frac{\pi}{2}t \right )+i\,sin\left (\frac{\pi}{2}t \right )\),\(0\leq t\leq 4\)

are all parametrizations, oriented in the positive direction, for the unit circle \(\left | z \right |=1\).