6.1: Applications of Conformal Mappings

Last updated
Save as PDF

Page ID: 76230

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Hydrodynamics

If we have a (steady-state) incompressible, nonviscous fluid, we are interested in finding its velocity field

\(\mathbf V (x,y)= \left(u(x,y), v(x,y)\right).\)

From vector analysis we know that ‘incompressible’ means that the divergence \(\text{div}\,\mathbf V =0.\) (We say \(\mathbf V\) is divergence free.) We assume that \(\mathbf V\) is also a potential flow and hence is circulation free; that is \(\mathbf V = \text{grad } \phi\) for some \(\phi\) called the velocity potential. Thus \(\phi\) is harmonic because

\(\nabla^2\phi = \text{div } \text{grad }\phi = \text{div } \mathbf V=0.\)

Thus when we solve for \(\phi\) we can obtain \(\mathbf V\) by taking \(\mathbf V = \text{grad } \phi\). That is

\(\begin{eqnarray*}
u=\frac{\partial \phi }{\partial x},\quad v=\frac{\partial \phi }{\partial y}.
\end{eqnarray*}\)

The conjugate \(ψ\) of the harmonic function \(ϕ\) (which will exist on any simple connected region) is called the stream function, and the analytic function

\(F=\phi +i\psi\)

is called the complex potential.

The stream function must satisfy

\(\begin{eqnarray*}
u=\frac{\partial \psi }{\partial y},\quad v=-\frac{\partial \psi }{\partial x}.
\end{eqnarray*}\)

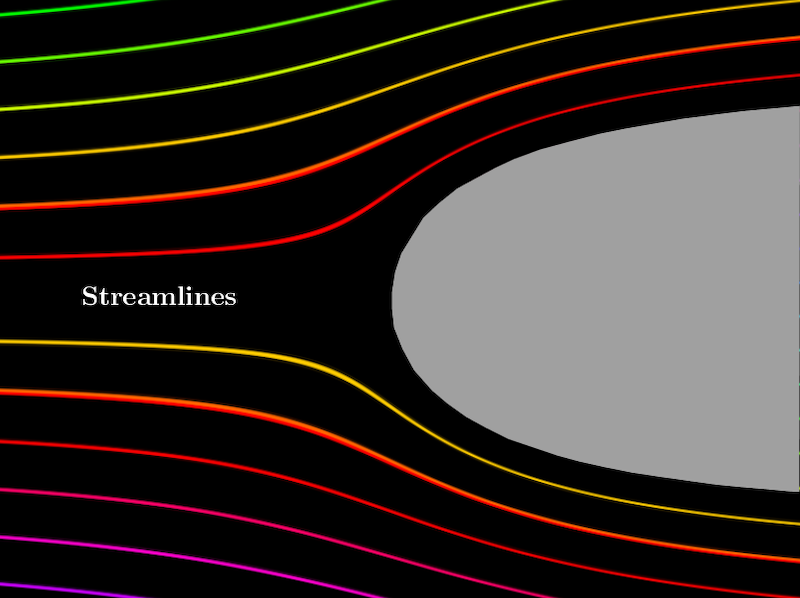
Finally, lines of constant \(ψ\) have \(V\) as their tangents, so lines of constant \(ψ\) may be interpreted as the lines along which particles of fluid move; hence the name stream function.