3.8: Extensions and Applications of Green’s Theorem
- Page ID
- 50594
Simply Connected Regions
A region \(D\) in the plane is simply connected if it has “no holes”. Said differently, it is simply connected for every simple closed curve \(C\) in \(D\), the interior of \(C\) is fully contained in \(D\).
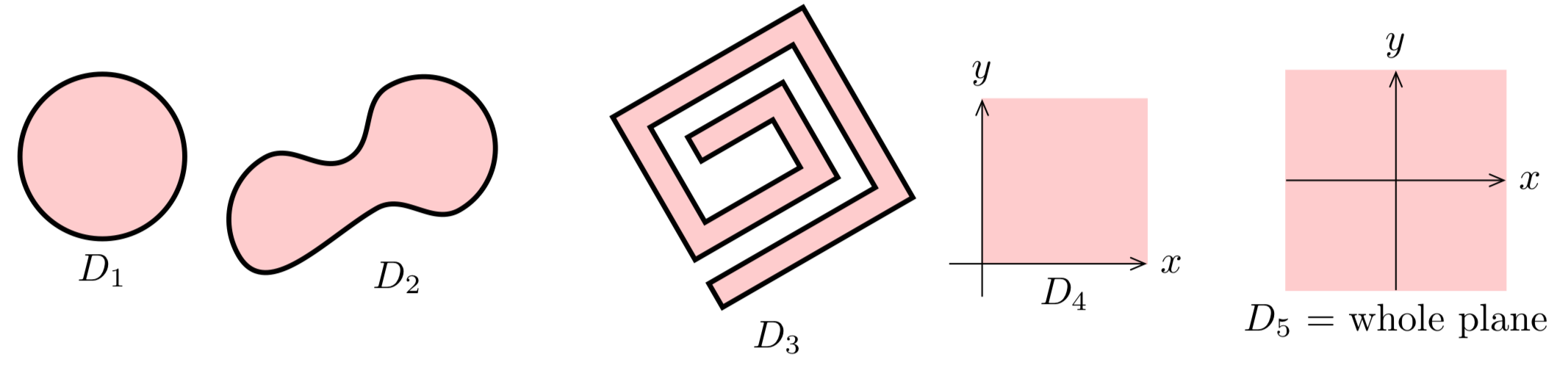
\(D_1\) - \(D_5\) are simply connected. For any simple closed curve \(C\) inside any of these regions the interior of \(C\) is entirely inside the region.
Note: Sometimes we say any curve can be shrunk to a point without leaving the region.
The regions below are not simply connected. For each, the interior of the curve \(C\) is not entirely in the region.
Potential Theorem
Here is an application of Green’s theorem which tells us how to spot a conservative field on a simply connected region. The theorem does not have a standard name, so we choose to call it the Potential Theorem.
Take \(F = (M, N)\) defined and differentiable on a region \(D\).
- If \(F = \nabla f\) then \(\text{curl}F = N_x - M_y = 0\).
- If \(D\) is simply connected and \(\text{curl} F = 0\) on \(D\), then \(F = \nabla f\) for some \(f\).
We know that on a connected region, being a gradient field is equivalent to being conservative. So we can restate the Potential Theorem as: on a simply connected region, \(F\) is conservative is equivalent to \(\text{curl} F = 0\).
- Proof
-
Proof of (a): \(F = (f_x, f_y)\), so \(\text{curl} F = f_{yx} - f_{xy} = 0\).
Proof of (b): Suppose \(C\) is a simple closed curve in \(D\). Since \(D\) is simply connected the interior of \(C\) is also in \(D\). Therefore, using Green’s theorem we have,
\[\oint_{C} F \cdot dr = \int \int_{R} \text{curl} F\ dA = 0. \nonumber \]
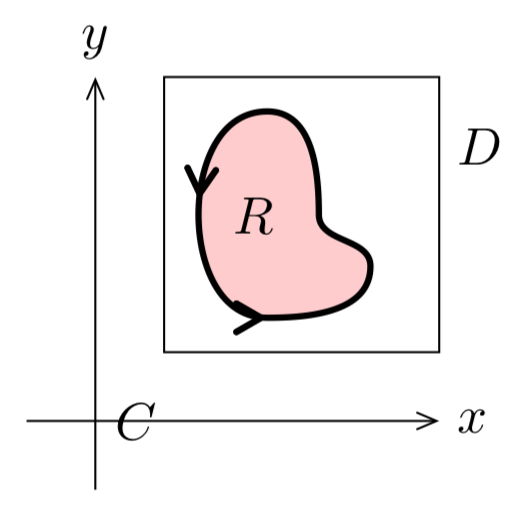
Figure \(\PageIndex{3}\): Potential Theorem This shows that \(F\) is conservative in \(D\). Therefore, this is a gradient field.
Summary: Suppose the vector field \(F = (M, N)\) is defined on a simply connected region \(D\). Then, the following statements are equivalent.
- \(\int_P^Q F \cdot dr\) is path independent.
- \(\oint_{C} F \cdot dr = 0\) for any closed path \(C\).
- \(F = \nabla f\) for some \(f\) in \(D\).
- \(F\) is conservative in \(D\).
If \(F\) is continuously differentiably then 1, 2, 3, 4 all imply 5: - \(\text{curl} F = N_x - M_y = 0\) in \(D\)
need simply connected in the Potential Theorem
If there is a hole then \(F\) might not be defined on the interior of \(C\). (Figure \(\PageIndex{4}\))
Extended Green’s Theorem
We can extend Green’s theorem to a region \(R\) which has multiple boundary curves.
Suppose \(R\) is the region between the two simple closed curves \(C_1\) and \(C_2\).
(Note \(R\) is always to the left as you traverse either curve in the direction indicated.)
Then we can extend Green’s theorem to this setting by
\[\oint_{C_1} F \cdot dr + \oint_{C_2} F \cdot dr = \int \int_R \text{curl} F \ dA. \nonumber \]
Likewise for more than two curves:
\[\oint_{C_1} F \cdot dr + \oint_{C_2} F \cdot dr + \oint_{C_3} F \cdot dr + \oint_{C_4} F \cdot dr = \int \int_R \text{curl} F \ dA. \nonumber \]
\(Proof\). The proof is based on the following figure. We ‘cut’ both \(C_1\) and \(C_2\) and connect them by two copies of \(C_3\), one in each direction. (In the figure we have drawn the two copies of \(C_3\) as separate curves, in reality they are the same curve traversed in opposite directions.)
Now the curve \(C = C_1+ C_3 + C_2 - C_3\) is a simple closed curve and Green’s theorem holds on it. But the region inside \(C\) is exactly \(R\) and the contributions of the two copies of \(C_3\) cancel. That is, we have shown that
\[\int \int_R \text{curl} F\ dA = \int_{C_1 + C_3 + C_2 - C_3} F \cdot dr = \int_{C_1 + C_2} F \cdot dr. \nonumber \]
This is exactly Green's theorem, which we wanted to prove.
Let \(F = \dfrac{(-y, x)}{r^2}\) ("tangential field")
\(F\) is defined on \(D\) = plane - (0, 0) = the punctured plane (Figure \(\PageIndex{7}\)).
It’s easy to compute (we’ve done it before) that \(\text{curl}F = 0\) in \(D\).
Question: For the tangential field \(F\) what values can \(\oint_{C} F \cdot dr\) take for \(C\) a simple closed curve (positively oriented)?
Solution
We have two cases (i) \(C_1\) not around 0 (ii) \(C_2\) around 0
In case (i) Green’s theorem applies because the interior does not contain the problem point at the origin. Thus,
\[\oint_{C_1} F \cdot dr = \int\int_R \text{curl} F\ dA = 0. \nonumber \]
For case (ii) we will show that
let \(C_3\) be a small circle of radius \(a\), entirely inside \(C_2\). By the extended Green’s theorem we have
\[\oint_{C_2} F \cdot dr - \oint_{C_3} F \cdot dr = \int\int_R \text{curl} F\ dA = 0. \nonumber \]
Thus, \(\oint_{C_2} F \cdot dr = \oint_{C_3} F \cdot dr\).
Using the usual parametrization of a circle we can easily compute that the line integral is
\[\int_{C_3} F \cdot dr = \int_{0}^{2\pi} 1 \ dt = 2\pi. \ \ \ \ QED. \nonumber \]
Answer to the question: The only possible values are 0 and \(2\pi\).
We can extend this answer in the following way:
If \(C\) is not simple, then the possible values of \(\oint_C F \cdot dr\) are \(2\pi n\), where \(n\) is the number of times \(C\) goes (counterclockwise) around (0,0).
Not for class: \(n\) is called the winding number of \(C\) around 0. \(n\) also equals the number of times \(C\) crosses the positive \(x\)-axis, counting +1 from below and -1 from above.


