5.2: Cauchy’s Integral Formula for Derivatives
- Page ID
- 6496
Cauchy’s integral formula is worth repeating several times. So, now we give it for all derivatives \(f^{(n)} (z)\) of \(f\). This will include the formula for functions as a special case.
If \(f(z)\) and \(C\) satisfy the same hypotheses as for Cauchy’s integral formula then, for all \(z\) inside \(C\) we have
\[f^{(n)} (z) = \dfrac{n!}{2 \pi i } \int_C \dfrac{f(w)}{(w - z)^{n + 1}} \ dw, \ \ n = 0, 1, 2, ... \nonumber \]
where, \(C\) is a simple closed curve, oriented counterclockwise, \(z\) is inside \(C\) and \(f(w)\) is analytic on and inside \(C\).
Evaluate \(I = \int_C \dfrac{e^{2z}}{z^4} \ dz\) where \(C : |z| = 1\).
Solution
With Cauchy’s formula for derivatives this is easy. Let \(f(z) = e^{2z}\). Then,
\[I = \int_C \dfrac{f(z)}{z^4} \ dz = \dfrac{2 \pi i} {3!} f''' (0) = \dfrac{8}{3} \pi i. \nonumber \]
Now let \(C\) be the contour shown below and evaluate the same integral as in the previous example.
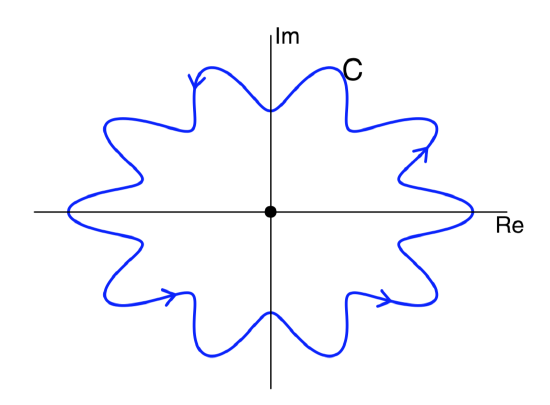
Solution
Again this is easy: the integral is the same as the previous example, i.e. \(I = \dfrac{8}{3} \pi i\).
Another approach to some basic examples
Suppose \(C\) is a simple closed curve around 0. We have seen that
\[\int_{C} \dfrac{1}{z} \ dz = 2 \pi i. \nonumber \]
The Cauchy integral formula gives the same result. That is, let \(f(z) = 1\), then the formula says
\[\dfrac{1}{2\pi i} \int_{C} \dfrac{f(z)}{z - 0}\ dz = f(0) = 1. \nonumber \]
Likewise Cauchy’s formula for derivatives shows
\[\int_{C} \dfrac{1}{(z)^n}\ dz = \int_{C} \dfrac{f(z)}{z^{n + 1}} \ dz = f^{(n)} (0) = 0, \text{ for integers } n > 1. \nonumber \]
More examples
Compute \(\int_C \dfrac{\cos (z)}{z(z^2 + 0)} \ dz\) over the contour shown.
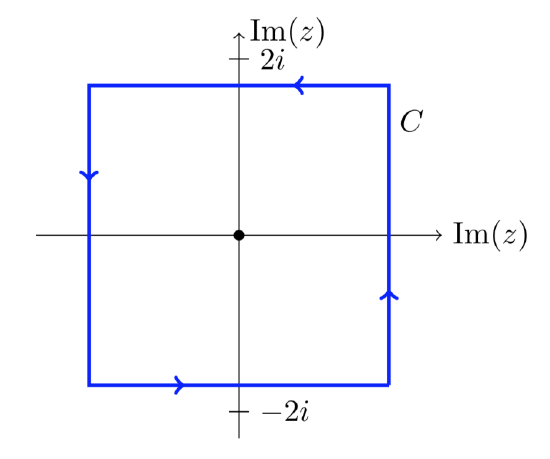
Solution
Let \(f(z) = \cos (z)/ (z^2 + 8)\). \(f(z)\) is analytic on and inside the curve \(C\). That is, the roots of \(z^2 + 8\) are outside the curve. So, we rewrite the integral as
\[\int_C \dfrac{\cos (z)/ (z^2 + 8)}{z} \ dz = \int_C \dfrac{f(z)}{z} \ dz = 2 \pi i f(0) = 2 \pi i \dfrac{1}{8} = \dfrac{\pi i}{4}. \nonumber \]
Compute \(\int_C \dfrac{1}{(z^2 + 4)^2}\ dz\) over the contour shown.
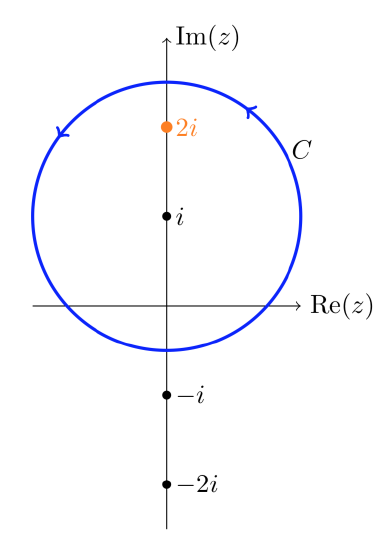
Solution
We factor the denominator as
\[\dfrac{1}{(z^2 + 4)^2} = \dfrac{1}{(z - 2i)^2 (z + 2i)^2}. \nonumber \]
Let
\[f(z) = \dfrac{1}{(z + 2i)^2}. \nonumber \]
Clear \(f(z)\) is analytic inside \(C\). So, by Cauchy’s formula for derivatives:
\[\int_C \dfrac{1}{(z^2 + 4)^2} \ dz = \int_C \dfrac{f(z)}{(z - 2i)^2} = 2 \pi i f'(2i) = 2\pi i [\dfrac{-2}{(z + 2i)^3}]_{z = 2i} = \dfrac{4 \pi i}{64 i} = \dfrac{\pi}{16} \nonumber \]
Compute \(\int_C \dfrac{z}{z^2 + 4} \ dz\) over the curve \(C\) shown below.
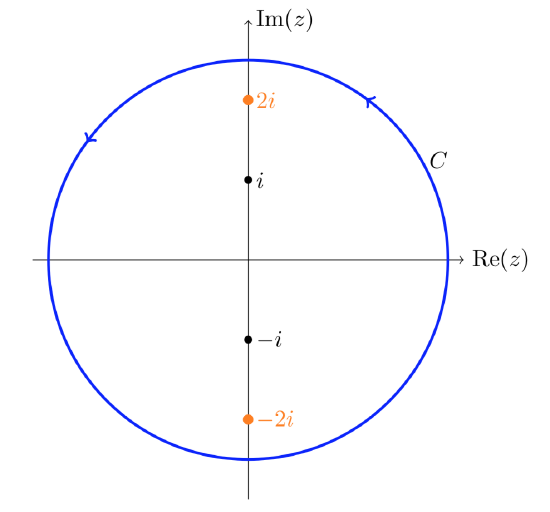
Solution
The integrand has singularities at \(\pm 2i\) and the curve \(C\) encloses them both. The solution to the previous solution won’t work because we can’t find an appropriate \(f(z)\) that is analytic on the whole interior of \(C\). Our solution is to split the curve into two pieces. Notice that \(C_3\) is traversed both forward and backward.
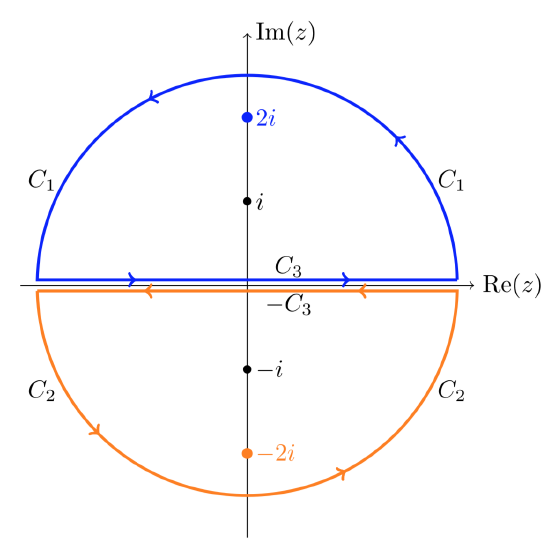
Split the original curve \(C\) into 2 pieces that each surround just one singularity.
We have
\[\dfrac{z}{z^2 + 4} = \dfrac{z}{(z - 2i)(z + 2i)}. \nonumber \]
We let
\[f_1 (z) = \dfrac{z}{z + 2i} \text{ and } f_2 (z) = \dfrac{z}{z - 2i}. \nonumber \]
So,
\[\dfrac{z}{z^2 + 4} = \dfrac{f_1(z)}{z - 2i} = \dfrac{f_2(z)}{z + 2i}. \nonumber \]
The integral, can be written out as
\[\int_{C} \dfrac{z}{z^2 + 4} \ dz = \int_{C_1 + C_3 - C_3 + C_2} \dfrac{z}{z^2 + 4} \ dz = \int_{C_1 + C_3} \dfrac{f_1 (z)}{z - 2i} \ dz + \int_{C_2 - C_3} \dfrac{f_2 (z)}{z + 2i} \ dz \nonumber \]
Since \(f_1\) is analytic inside the simple closed curve \(C_1 + C_3\) and \(f_2\) is analytic inside the simple closed curve \(C_2 - C_3\), Cauchy’s formula applies to both integrals. The total integral equals
\[2\pi i (f_1(2i) + f_2 (-2i)) = 2\pi i (1/2 + 1/2) = 2\pi i. \nonumber \]
Remarks. 1. We could also have done this problem using partial fractions:
\[\dfrac{z}{(z - 2i) (z + 2i)} = \dfrac{A}{z - 2i} + \dfrac{B}{z + 2i}. \nonumber \]
It will turn out that \(A = f_1 (2i)\) and \(B = f_2(-2i)\). It is easy to apply the Cauchy integral formula to both terms.
2. Important note. In an upcoming topic we will formulate the Cauchy residue theorem. This will allow us to compute the integrals in Examples 5.3.3-5.3.5 in an easier and less ad hoc manner.
triangle inequality for integrals
We discussed the triangle inequality in the Topic 1 notes. It says that
\[|z_1 + z_2| \le |z_1| + |z_2|, \nonumber \]
with equality if and only if \(z_1\) and \(z_2\) lie on the same ray from the origin.
A useful variant of this statement is
\[|z_1| - |z_2| \le |z_1 - z_2|. \nonumber \]
This follows because Equation 5.3.17 implies
\[|z_1| = |(z_1 - z_2) + z_2| \le |z_1 - z_2| + |z_2|. \nonumber \]
Now substracting \(z_2\) from both sides give Equation 5.3.18
Since an integral is basically a sum, this translates to the triangle inequality for integrals. We’ll state it in two ways that will be useful to us.
Suppose \(g(t)\) is a complex valued function of a real variable, defined on \(a \le t \le b\). Then
\[|\int_{a}^{b} g(t) \ dt| \le \int_{a}^{b} |g(t)|\ dt, \nonumber \]
with equality if and only if the values of \(g(t)\) all lie on the same ray from the origin.
- Proof
-
This follows by approximating the integral as a Riemann sum.
\[|\int_{a}^{b} g(t)\ dt| \approx |\sum g(t_k) \Delta t| \le \sum |g(t_k)| \Delta t \approx \int_{a}^{b} |g(t)|\ dt. \nonumber \]
The middle inequality is just the standard triangle inequality for sums of complex numbers.
For any function \(f(z)\) and any curve \(\gamma\), we have
\[|\int_{\gamma} f(z)\ dz| \le \int_{\gamma} |f(z)|\ |dz|. \nonumber \]
Here \(dz = \gamma ' (t)\ dt\) and \(|dz| = |\gamma ' (t)|\ dt\).
- Proof
-
This follows immediately from the previous theorem:
\[|\int_{\gamma} f(z)\ dz| = |\int_{a}^{b} f(\gamma (t)) \gamma ' (t)\ dt| \le \int_{a}^{b} |f(\gamma (t))|\ |\gamma ' (t)| \ dt = \int_{\gamma} |f(z)|\ |dz|. \nonumber \]
If \(|f(z)| < M\) on \(C\) then
\[|\int_C f(z)\ dz| \le M \cdot \text{(length of } C). \nonumber \]
- Proof
-
Let \(\gamma (t)\), with \(a \le t \le b\), be a parametrization of \(C\). Using the triangle inequality
\[|\int_C f(z)\ dz| \le \int_C |f(z)|\ |dz| = \int_{a}^{b} |f(\gamma (t))|\ |\gamma '(t)|\ dt \le \int_{a}^{b} M|\gamma ' (t)|\ dt = M \cdot \text{(length of } C). \nonumber \]
Here we have used that
\[|\gamma ' (t)|\ dt = \sqrt{(x')^2 + (y')^2} \ dt = ds, \nonumber \]
the arclength element.
Compute the real integral
\[I = \int_{-\infty}^{\infty} \dfrac{1}{(x^2 + 1)^2}\ dx \nonumber \]
Solution
The trick is to integrate \(f(z) = 1/(z^2 + 1)^2\) over the closed contour \(C_1 + C_R\) shown, and then show that the contribution of \(C_R\) to this integral vanishes as \(R\) goes to \(\infty\).
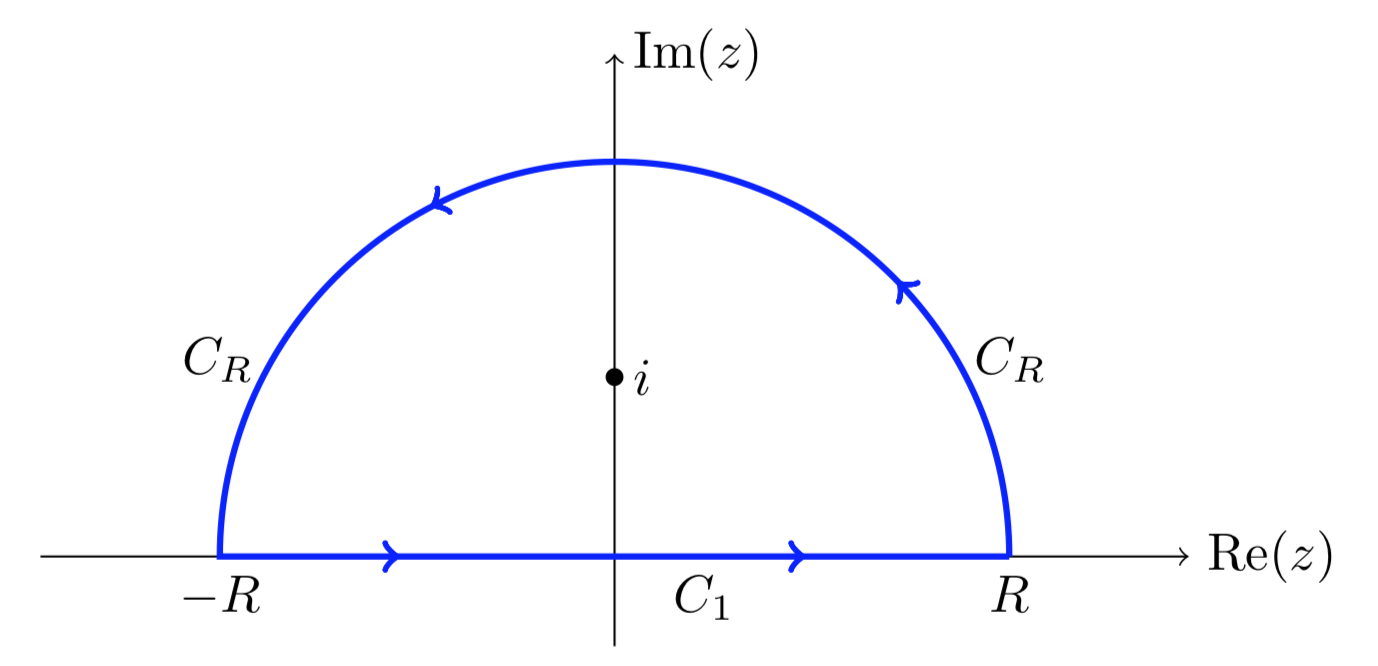
The only singularity of
\[f(z) = \dfrac{1}{(z + i)^2 (z - i)^2} \nonumber \]
inside the contour is at \(z = i\). Let
\[g(z) = \dfrac{1}{(z + i)^2}. \nonumber \]
Since \(g\) is analytic on and inside the contour, Cauchy’s formula gives
\[\int_{C_1 + C_R} f(z)\ dz = \int_{C_1 + C_R} \dfrac{g(z)}{(z - i)^2}\ dz = 2\pi i g'(i) = 2\pi i \dfrac{-2}{(2i)^3} = \dfrac{\pi}{2}. \nonumber \]
We parametrize \(C_1\) by
\[\gamma (x) = x, \text{ with } -R \le x \le R. \nonumber \]
So,
\[\int_{C_1} f(z)\ dz = \int_{-R}^{R} \dfrac{1}{(x^2 + 1)^2}\ dx. \nonumber \]
This goes to \(I\) (the value we want to compute) as \(R \to \infty\).
Next, we parametrize \(C_R\) by
\[\gamma (\theta) = R e^{i \theta}, \text{ with } 0 \le \theta \le \pi. \nonumber \]
So,
\[\int_{C_R} f(z) \ dz = \int_{0}^{\pi} \dfrac{1}{(R^2 e^{2i \theta} + 1)^2} i Re^{i \theta} \ d \theta \nonumber \]
By the triangle inequality for integrals, if \(R > 1\)
\[|\int_{C_R} f(z)\ dz| \le \int_{0}^{\pi} |\dfrac{1}{(R^2 e^{2i \theta} + 1)^2} iRe^{i \theta}|\ d\theta. \nonumber \]
From the triangle equality in the form Equation 5.3.18 we know that
\[|R^2 e^{2i \theta} + 1| \ge |R^2 e^{2i \theta}| - |1| = R^2 - 1. \nonumber \]
Thus,
\[\dfrac{1}{|R^2 e^{2i \theta} + 1|} \le \dfrac{1}{R^2 - 1} \ \ \Rightarrow \ \ \dfrac{1}{|R^2 e^{2i \theta} + 1|^2} \le \dfrac{1}{(R^2 - 1)^2}. \nonumber \]
Using Equation 5.3.34, we then have
\[|\int_{C_R} f(z) \ dz| \le \int_{0}^{\pi} |\dfrac{1}{(R^2 e^{2i \theta} + 1)^2} iRe^{i \theta}|\ d\theta \le \int_{0}^{\pi} \dfrac{R}{(R^2 - 1)^2}\ d\theta = \dfrac{1}{(R^2 - 1)^2}. \nonumber \]
Clearly this goes to 0 as \(R\) goes to infinity. Thus, the integral over the contour \(C_1 + C_R\) goes to \(I\) as \(R\) gets large. But
\[\int_{C_1 + C_R} f(z) \ dz = \pi /2 \nonumber \]
for all \(R > 1\). We can therefore conclude that \(I = \pi /2\).
As a sanity check, we note that our answer is real and positive as it needs to be.


