13.8: Laplace inverse
- Page ID
- 51238
Up to now we have computed the inverse Laplace transform by table lookup. For example, \(\mathcal{L}^{-1} (1/(s - a)) = e^{at}\). To do this properly we should first check that the Laplace transform has an inverse.
We start with the bad news: Unfortunately this is not strictly true. There are many functions with the same Laplace transform. We list some of the ways this can happen.
- If \(f(t) = g(t)\) for \(t \ge 0\), then clearly \(F(s) = G(s)\). Since the Laplace transform only concerns \(t \ge 0\), the functions can differ completely for \(t < 0\).
- Suppose \(f(t) = e^{at}\) and
\[g(t) = \begin{cases} f(t) & \text{ for } t \ne 1 \\ 0 & \text{ for } t = 1. \end{cases} \nonumber \]
That is, \(f\) and \(g\) are the same except we arbitrarily assigned them different values at \(t = 1\). Then, since the integrals won’t notice the difference at one point, \(F(s) = G(s) = 1/(s - a)\). In this sense it is impossible to define \(\mathcal{L}^{-1} (F)\) uniquely.
The good news is that the inverse exists as long as we consider two functions that only differ on a negligible set of points the same. In particular, we can make the following claim.
Suppose \(f\) and \(g\) are continuous and \(F(s) = G(s)\) for all \(s\) with \(\text{Re} (s) > a\) for some \(a\). Then \(f(t) = g(t)\) for \(t \ge 0\).
This theorem can be stated in a way that includes piecewise continuous functions. Such a statement takes more care, which would obscure the basic point that the Laplace transform has a unique inverse up to some, for us, trivial differences.
We start with a few examples that we can compute directly.
Let
\[f(t) = e^{at}. \nonumber \]
So,
\[F(s) = \dfrac{1}{s - a}. \nonumber \]
Show
\[f(t) = \sum \text{Res} (F(s) e^{st}) \nonumber \]
\[f(t) = \dfrac{1}{2\pi i} \int_{c - i\infty}^{c + i \infty} F(s) e^{st}\ ds \nonumber \]
The sum is over all poles of \(e^{st}/(s - a)\). As usual, we only consider \(t > 0\).
Here, \(c > \text{Re} (a)\) and the integral means the path integral along the vertical line \(x = c\).
Solution
Proving Equation 13.8.4 is straightforward: It is clear that
\[\dfrac{e^{st}}{s -a} \nonumber \]
has only one pole which is at \(s = a\). Since,
\[\sum \text{Res} (\dfrac{e^{st}}{s - a}, a) = e^{at} \nonumber \]
we have proved Equation 13.8.4.
Proving Equation 13.8.5 is more involved. We should first check the convergence of the integral. In this case, \(s = c + iy\), so the integral is
\[\dfrac{1}{2\pi i} \int_{c - i \infty}^{c + i \infty} F(s) e^{st} \ ds = \dfrac{1}{2\pi i} \int_{-\infty}^{\infty} \dfrac{e^{(c + iy)t}}{c + iy - a} i \ dy = \dfrac{e^{ct}}{2 \pi} \int_{-\infty}^{\infty} \dfrac{e^{iyt}}{c + iy - a} \ dy. \nonumber \]
The (conditional) convergence of this integral follows using exactly the same argument as in the example near the end of Topic 9 on the Fourier inversion formula for \(f(t) = e^{at}\). That is, the integrand is a decaying oscillation, around 0, so its integral is also a decaying oscillation around some limiting value.
Now we use the contour shown below.
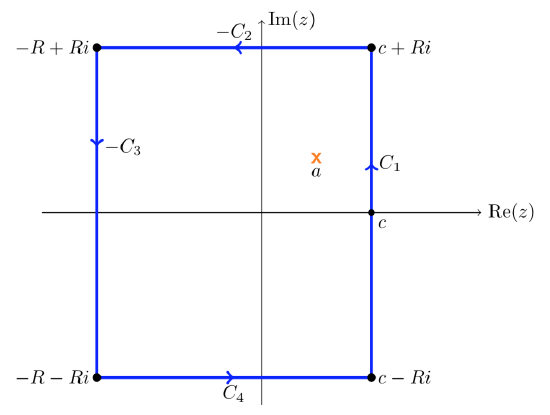
We will let \(R\) go to infinity and use the following steps to prove Equation 13.8.5.
- The residue theorem guarantees that if the curve is large enough to contain \(a\) then
\[\dfrac{1}{2\pi i} \int_{C_1 - C_2 - C_3 + C_4} \dfrac{e^{st}}{s - a}\ ds = \sum \text{Res} (\dfrac{e^{st}}{s - a}, a) = e^{at}. \nonumber \] - In a moment we will show that the integrals over \(C_2, C_3, C_4\) all go to 0 as \(R \to \infty\).
- Clearly as \(R\) goes to infinity, the integral over \(C_1\) goes to the integral in Equation 13.8.5 Putting these steps together we have
\[e^{at} = \lim_{R \to \infty} \int_{C_1 - C_2 - C_3 + C_4} \dfrac{e^{st}}{s - a} \ ds = \int_{c - i\infty}^{c + i\infty} \dfrac{e^{st}}{s - a} \ ds \nonumber \]
Except for proving the claims in step 2, this proves Equation 13.8.5.
To verify step 2 we look at one side at a time.
\(C_2\): \(C_2\) is parametrized by \(s = \gamma (u) = u + iR\), with \(-R \le u \le c\). So,
\[|\int_{C_2} \dfrac{e^{st}}{s - a} \ ds| = \int_{-R}^{c} |\dfrac{e^{(u + iR)t}}{u + iR - a}| \le \int_{-R}^{c} \dfrac{e^{ut}}{R} \ du = \dfrac{e^{ct} - e^{-Rt}}{tR}. \nonumber \]
Since \(c\) and \(t\) are fixed, it’s clear this goes to 0 as \(R\) goes to infinity.
The bottom \(C_4\) is handled in exactly the same manner as the top \(C_2\).
\(C_3\): \(C_3\) is parametrized by \(s = \gamma (u) = -R + iu\), with \(-R \le u \le R\). So,
\[|\int_{C_3} \dfrac{e^{st}}{s - a} \ ds| = \int_{-R}^{R} |\dfrac{e^{(-R + iu)t}}{-R + iu - a}| \le \int_{-R}^{R} \dfrac{e^{-Rt}}{R + a} \ du = \dfrac{e^{-Rt}}{R + a} \int_{-R}^{R} \ du = \dfrac{2\text{Re}^{-Rt}}{R+a}. \nonumber \]
Since \(a\) and \(t > 0\) are fixed, it’s clear this goes to 0 as \(R\) goes to infinity.
Repeat the previous example with \(f(t) = t\) for \(t > 0\), \(F(s) = 1/s^2\).
This is similar to the previous example. Since \(F\) decays like \(1/s^2\) we can actually allow \(t \ge 0\)
Assume \(f\) is continuous and of exponential type \(a\). Then for \(c > a\) we have
\[f(t) = \dfrac{1}{2\pi i} \int_{c - i\infty}^{c + i\infty} F(s) e^{st}\ ds. \nonumber \]
As usual, this formula holds for \(t > 0\).
- Proof
-
The proof uses the Fourier inversion formula. We will just accept this theorem for now. Example 13.8.1 above illustrates the theorem.
Suppose \(F(s)\) has a finite number of poles and decays like \(1/s\) (or faster). Define
\[f(t) = \sum \text{Res} (F(s) e^{st}, p_k), \text{ where the sum is over all the poles } p_k. \nonumber \]
Then \(\mathcal{L} (f; s) = F(s)\)
- Proof
-
Proof given in class. To be added here. The basic ideas are present in the examples above, though it requires a fairly clever choice of contours.
The integral inversion formula in Equation 13.8.13 can be viewed as writing \(f(t)\) as a ‘sum’ of exponentials. This is extremely useful. For example, for a linear system if we know how the system responds to input \(f(t) = e^{at}\) for all \(a\), then we know how it responds to any input by writing it as a ‘sum’ of exponentials.