4.E: Hyperbolic Equations (Exercises)



\[u_{tt}=c^2u_{xx}\]

\[u(A)+u(C)=u(B)+u(D) \]

holds for all parallelograms \(ABCD\) in the \((x,t)\)-plane, which are bounded by characteristic lines, see Figure 4.E.1.

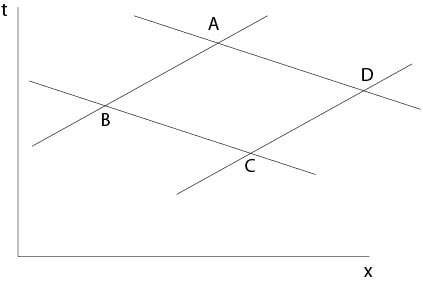
Figure 4.1: Figure to the exercise

Q4.2: Method of separation of variables

Let \(v_k(x)\) be an eigenfunction to the eigenvalue of the eigenvalue problem

\(-v''(x)=\lambda v(x)\) in \((0,l)\), \(v(0)=v(l)=0\)

and let \(w_k(t)\) be a solution of differential equation

\[-w''(t)=\lambda_kw(t)\]

Prove that \(v_k(x)w_k(t)\) is a solution of the partial differential equation (wave equation) \(u_{tt}=u_{xx}\).

Q4.3

Solve for given \(f(x)\) and \(\mu\in\mathbb{R}^1\) the initial value problem

\begin{eqnarray*}
u_t+u_x+\mu u_{xxx} &=& 0\quad \mbox{in}\quad \mathbb{R}^1\times\mathbb{R}^1_+\\
u(x,0) &=& f(x) \ .
\end{eqnarray*}

Q4.4

Let \(S:= \{(x,t);\ t=\gamma x\}\) be space-like, i.e., \(|\gamma|<1/c^2\)) in \((x,t)\)-space, \(x=(x_1,x_2,x_3)\). Show that the Cauchy initial value problem \(\Box u=0\) with data for \(u\) on \(S\) can be transformed using the Lorentz-transform

\[x_1={x_1-\gamma c^2t\over\sqrt{1-\gamma^2c^2}}\]

\[\ x_2'=x_2,\ x_3'=x_3\]

\[t'={t-\gamma x_1\over\sqrt{1-\gamma^2c^2}}\]

into the initial value problem, in new coordinates,

\begin{eqnarray*}
\Box u &=& 0\\
u(x',0) &=& f(x')\\
u_{t'}(x',0) &=& g(x')\ .
\end{eqnarray*}

Here we denote the transformed function by \(u\) again.

Q4.5

\[ u(x,t):=\sum_{n=1}^\infty\alpha_n\cos\left(\dfrac{\pi n}{l} t\right)\sin\left(\dfrac{\pi n}{l} x\right) \]

is a \(C^2\)-solution of the wave equation \(u_{tt}=u_{xx}\) if \(|\alpha_n|\le c/n^ 4\), where the constant \(c\) is independent of \(n\).

(ii) Set

\[\alpha_n:=\int_0^ l f(x)\sin\left(\dfrac{\pi n}{l} x\right)\ dx.\]

Prove \(|\alpha_n|\le c/n^4\), provided \(f\in C^4_0(0,l)\).

Q4.6

Let \(\Omega\) be the rectangle \((0,a)\times (0,b)\). Find all eigenvalues and associated eigenfunctions of \(-\triangle u=\lambda u\) in \(\Omega\), \(u=0\) on \(\partial\Omega\). Hint: Separation of variables.

Q4.7

\[i\hbar\psi_t=-\dfrac{\hbar^2}{2m}\triangle_x\psi + V(x)\psi\quad \mbox{in}\ \mathbb{R}^n\times\mathbb{R}^1,\]

\[\int_\mathbb{R}^n|\psi(x,t)|^2dx=1\ ,\]

\[\triangle u+\dfrac{2m}{\hbar^2}(E-V(x))u=0\quad\mbox{in}\ \ \mathbb{R}^n\]

under the side condition \(\int_\mathbb{R}^n |u|^2 dx =1\), \(u:\ \mathbb{R}^n\mapsto
{\mathbb C}\).

Here is

\[\psi:\ \mathbb{R}^n\times\mathbb{R}^1\mapsto{\mathbb C}\]

Planck's constant (\(\hbar\)) is a small positive constant) and \(V(x)\) a given potential.

Remark. In the case of a hydrogen atom the potential is \(V(x)=-e/|x|\), \(e\) is here a positive constant. Then eigenvalues are given by \(E_n=-me^4/(2\hbar^2n^2)\), \(n\in{\mathbb N}\), see [22], pp. 202.

Q4.8

Find nonzero solutions by using separation of variables of \(u_{tt}=\triangle_xu\) in \(\Omega\times (0,\infty)\), \(u(x,t)=0\) on \(\partial\Omega\), where \(\Omega\) is the circular cylinder \(\Omega=\{(x_1,x_2,x_3)\in\mathbb{R}^n:\ x_1^2+x_2^2<R^2,\ 0<x_3<h\}\).

Q4.9

Solve the initial value problem

\begin{eqnarray*}
3u_{tt}-4u_{xx} &=& 0\\
u(x,0) &=& \sin x \\
u_t(x,0) &=& 1\ .
\end{eqnarray*}

Q4.10

Solve the initial value problem

\begin{eqnarray*}
u_{tt}-c^2u_{xx} &=& x^2,\ t>0,\ x\in \mathbb{R}^1\\
u(x,0) &=& x \\
u_t(x,0) &=& 0\ .
\end{eqnarray*}

Hint: Find a solution of the differential equation independent on \(t\), and transform the above problem into an initial value problem with homogeneous differential equation by using this solution.

Q4.11

Find with the method of separation of variables nonzero solutions \(u(x,t)\), \(0\le x\le1,\ 0\le t<\infty,\) of

\[ u_{tt}-u_{xx}+u=0\ ,\]

such that \(u(0,t)=0\), and \(u(1,t)=0\) for all \(t\in[0,\infty)\).

Q4.12

\[u_{tt}-c^2u_{xx}=\lambda^2u,\ \lambda=const.\]

\[u(x,t)=f(x^2-c^2t^2)=f(s),\ s:=x^2-c^2t^2\]

\[ z^2f''(z)+zf'(z)+(z^2-n^2)f=0,\ z>0 \]

with \(n=0\).

Remark. The above differential equation for \(u\) is the transformed telegraph equation (see Section 4.4).

Q4.13

Find the formula for the solution of the following Cauchy initial value problem \(u_{xy}=f(x,y)\), where \(S\): \(y=ax+b\), \(a>0\), and the initial conditions on \(S\) are given by

\begin{eqnarray*}
u&=&\alpha x +\beta y+\gamma,\\
u_x&=&\alpha,\\
u_y&=&\beta,
\end{eqnarray*}

\(a,\ b,\ \alpha,\ \beta,\ \gamma\) constants.

Q4.14

Find all eigenvalues \(\mu\) of

\begin{eqnarray*}
-q''(\theta)&=&\mu q(\theta)\\
q(\theta)&=&q(\theta+2\pi)\ .
\end{eqnarray*}

Contributors and Attributions

• Prof. Dr. Erich Miersemann (Universität Leipzig)

• Integrated by Justin Marshall.