5.4: CHAPTER 4

Exercise \(4.1.10\).

Answer

Use the identity \[\lim _{n \rightarrow \infty}\left(\frac{f\left(a+\frac{1}{n}\right)}{f(a)}\right)^{n}=\lim _{n \rightarrow \infty} \exp \left(n\left[\ln \left(f\left(a+\frac{1}{n}\right)\right)-\ln (f(a)]\right)\right. .\]

Exercise \(4.1.11\).

Answer

1. Using the differentiability of \(\sin x\) and Theorem 4.1.3, we conclude the function is differentiable at any \(a \neq 0\). So, we only need to show the differentiability of the function at \(a = 0\) By the definition of the derivative, consider the limit \[\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=\lim _{x \rightarrow 0} \frac{x^{2} \sin (1 / x)+c x}{x}=\lim _{x \rightarrow 0}[x \sin (1 / x)+c] .\] For any \(x \neq 0\), we have \[|x \sin (1 / x)|=|x||\sin (1 / x)| \leq|x| ,\] which implies \[-|x| \leq x \sin (1 / x) \leq|x| .\] Since \(\lim _{x \rightarrow 0}(-|x|)=\lim _{x \rightarrow 0}|x|=0\), applying the squeeze theorem yields \[\lim _{x \rightarrow 0} x \sin (1 / x)=0 .\] It now follows that \[f^{\prime}(0)=\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=\lim _{x \rightarrow 0}[x \sin (1 / x)+c]=c .\] Using Theorem 4.1.3 and the fact that \(\cos x\) is the derivative of \(\sin x\), the derivative of \(f\) can be written explicitly as \[f^{\prime}(x)=\left\{\begin{array}{ll}
   2 x \sin \frac{1}{x}-\cos (1 / x)+c, & \text { if } x \neq 0 \text {;}\\
   c, & \text { if } x=0 \text {.}
   \end{array}\right.\]

From the solution, it is important to see that the conclusion remains valid if we replace the function \(f\) by \[g(x)=\left\{\begin{array}{ll}
x^{n} \sin \frac{1}{x}, & \text { if } x \neq 0 \text {;}\\
0, & \text { if } x=0 \text {.}
\end{array}\right.\] where \(n \geq 2\), \(n \in \mathbb{N}\). Note that the function \(h(x) = cx\) does not play any role in the differentiability of \(f\).

We can generalize this problem as follows. Let \(\varphi\) be a bounded function on \(\mathbb{R}\), i.e., there is \(M > 0\) such that \[|\varphi(x)| \leq M \text { for all } x \in \mathbb{R} .\] Define the function \[f(x)=\left\{\begin{array}{ll}
x^{n} \varphi(1 / x), & \text { if } x \neq 0 \text {;}\\
0, & \text { if } x=0 \text {,}
\end{array}\right.\] where \(n \geq 2\), \(n \in \mathbb{N}\). Then \(f\) is differentiable at \(a = 0\).

Similar problems:

1. Show that the functions below are differentiable on \(\mathbb{R}\): \[f(x)=\left\{\begin{array}{ll}
   x^{3 / 2} \cos (1 / x), & \text { if } x \geq 0 \text{;}\\
   0, & \text { if } x<0
   \end{array}\right.\] and \[f(x)=\left\{\begin{array}{ll}
   x^{2} e^{-1 / x^{2}}, & \text { if } x \neq 0 \text {;}\\
   0, & \text { if } x=0 \text {.}
   \end{array}\right.\]
2. Suppose that \(\varphi\) is bounded and differentiable on \(\mathbb{R}\). Define the function \[f(x)=\left\{\begin{array}{ll}
   x^{2} e^{-1 / x^{2}}, & \text { if } x \neq 0 \text {;}\\
   0, & \text { if } x=0 \text {.}
   \end{array}\right.\] Show that if \(n \geq 2\), the function is differentiable on \(\mathbb{R}\) and find its derivative. Show that if \(n = 1\) and \(\lim _{x \rightarrow \infty} \varphi(x)\) does not exists, then \(f\) is not differentiable at \(0\).

2. Hint: Observe that \[\lim _{x \rightarrow \infty} \varphi(x) .\]

Exercise \(4.2.1\).

Answer

Define the function \[h(x) = f(x) - g(x).\] Then \(h\) has an absolute maximum at \(x_{0}\). Thus, \[h^{\prime}\left(x_{0}\right)=f^{\prime}\left(x_{0}\right)-g^{\prime}\left(x_{0}\right)=0 ,\] which implies \(f^{\prime}\left(x_{0}\right)=g^{\prime}\left(x_{0}\right)\).

Exercise \(4.2.3\).

Answer

The inequality holds obviously if \(a = b\). In the case where \(a \neq b\), the equality can be rewritten as \[\left|\frac{\sin (b)-\sin (a)}{b-a}\right| \leq 1 .\] The quotient \(\left|\frac{\sin (b)-\sin (a)}{b-a}\right|\) is the slope of the line connecting \((a, f(a))\) and \((b, f(b))\). We need to show that the absolute value of the slope is always beounded by \(1\), which can also be seen from the figure. The quotient also reminds us of applying the Mean Value Theorem for the function \(f(x) = \sin (x)\).

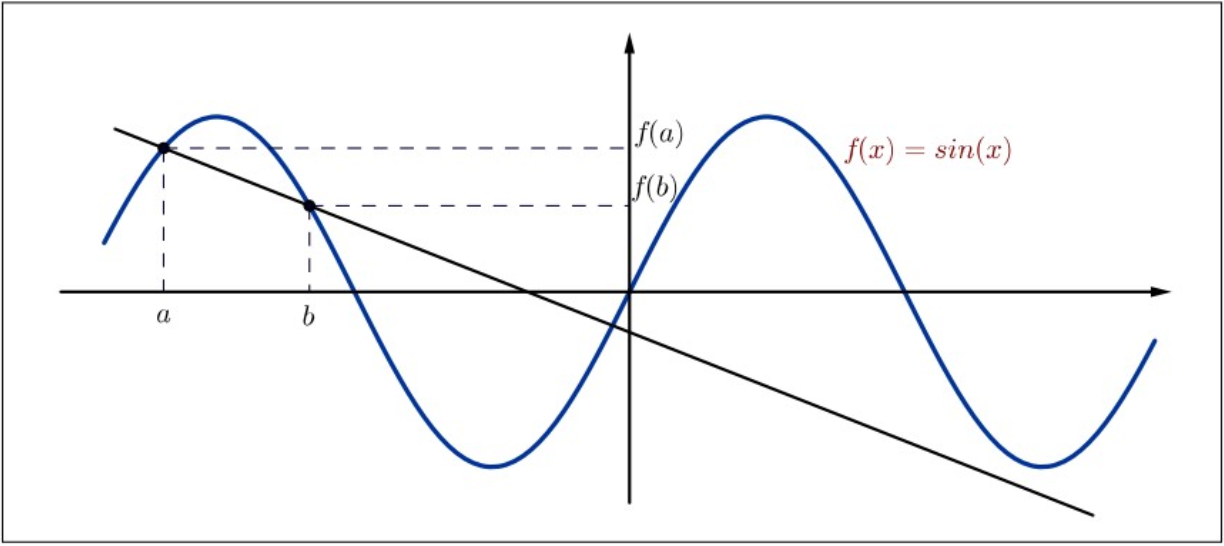
Figure \(5.1\): The function \(f(x) = \sin (x)\).

Consider the case where \(a < b\) and define the function \(f:[a, b] \rightarrow \mathbb{R}\) by \(f(x) = \sin (x)\). Clearly, the function satisfies all assumptions of the Mean Value Theorem on this interval with \(f^{\prime}(x)=\cos (x)\) for all \(x \in (a, b)\).

By the Mean Value Theorem, there exists \(c \in (a, b)\) such that \[\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)=\cos (c) ,\] which implies \[\left|\frac{f(b)-f(a)}{b-a}\right|=|\cos (c)| \leq 1 .\] It follows that \(|f(a)-f(b)| \leq|a-b|\). The solution is similar for the case where \(a > b\).

It is essential to realize that the most important property required in solving this problem is the boundedness of the derivative fo the function. Thus, it is possible to solve the following problems with a similar strategy.

1. Prove that \(|\cos (a)-\cos (b)| \leq|a-b|\) for all \(a, b \in \mathbb{R}\).
2. Prove that \(\left|\ln \left(1+e^{2 a}\right)-\ln \left(1+e^{2 b}\right)\right| \leq 2|a-b|\) for all \(a, b \in \mathbb{R}\).

Exercise \(4.2.4\).

Answer

Let us define \(f:[-\pi, \pi] \rightarrow \mathbb{R}\) by \[f(x)=x+\sum_{k=1}^{n}\left(a_{k} \sin k x+b_{k} \cos k x\right) .\] We want to find \(c \in(-\pi, \pi)\) such that \(f(c) = 0\).

Now, consider the function \[g(x)=\frac{x^{2}}{2}+\sum_{k=1}^{n}\left(-a_{k} \frac{\cos (k x)}{k}+b_{k} \frac{\sin (k x)}{k}\right) .\] Observe that \(g(-\pi)=g(\pi)\) and \(g^{\prime} = f\). The conclusion follows from Rolle's Theorem.

Exercise \(4.2.5\).

Answer

Use the identity \[\frac{1}{g(b)-g(a)}\left|\begin{array}{cc}
f(a) & f(b) \\
g(a) & g(b)
\end{array}\right|=\frac{f(a) g(b)-f(b) g(a)}{g(b)-g(a)}=\frac{\frac{f(a)}{g(a)}-\frac{f(b)}{g(b)}}{\frac{1}{g(a)}-\frac{1}{g(b)}} .\] Then apply the Cauchy mean value theorem for two functions \(\phi(x)=\frac{f(x)}{g(x)}\) and \(\psi(x)=\frac{1}{g(x)}\) on the interval \([a, b]\).

Exercise \(4.2.6\).

Answer

1. Given \(\varepsilon > 0\), first find \(x_{0}\) large enough so that \(\psi(x)=\frac{1}{g(x)}\) for \(x > x_{0}\). Then use the identity \[\frac{f(x)}{x}=\frac{f(x)-f\left(x_{0}\right)+f\left(x_{0}\right)}{x-x_{0}+x_{0}}=\frac{\frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}+\frac{f\left(x_{0}\right)}{x-x_{0}}}{1+\frac{x_{0}}{x-x_{0}}} ,\] and the mean value theorem to show that, for \(x\) large, \[a-\varepsilon<\frac{f(x)}{x}<a+\varepsilon .\]
2. Use the method in part (a).
3. Consider \(f(x) = \sin (x)\).

Exercise \(4.3.2\).

Answer

1. We can prove that \(f\) is uniformly continuous on \(\mathbb{R}\) by definition. given any \(\varepsilon > 0\), choose \(\delta=\left(\frac{\varepsilon}{\ell+1}\right)^{\frac{1}{\alpha}}\) and get \[|f(u)-f(v)| \leq \ell|u-v|^{\alpha}<\ell \delta^{\alpha}=\ell \frac{\varepsilon}{\ell+1}<\varepsilon\] whenever \(|u-v|<\delta\). Note that we use \(\ell + 1\) here instead of \(\ell\) to avoid the case where \(\ell = 0\).
2. We will prove that \(f\) is a constant function by showing that it is differentiable on \(\mathbb{R}\) and \(f^{\prime}(a)=0\) for all \(a \in \mathbb{R}\). Fix any \(a \in \mathbb{R}\). Then, for \(x \neq a\), \[\left|\frac{f(x)-f(a)}{x-a}\right| \leq \frac{\ell|x-a|^{\alpha}}{|x-a|}=\ell|x-a|^{\alpha-1} .\] Since \(\alpha > 1\), by the squeeze theorem, \[\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=0 .\] This implies that \(f\) is differentiable at \(a\) and \(f^{\prime}(a)=0\).
3. We can verify that the function \(f(x) = |x|\) satisfies the requirement.

From this problem, we see that it is only interesting to consider the class of functions that satisfy (4.8) when \(\alpha \leq 1\). It is an exercise to show that the function \(f(x)=|x|^{1 / 2}\) satisfies this condition with \(\ell = 1\) and \(\alpha=1 / 2\).

Exercise \(4.3.3\).

Answer

Define the function \[h(x)=g(x)-f(x) .\] Then \(h^{\prime}(x)=g^{\prime}(x)-f^{\prime}(x) \geq 0\) for all \(x \in\left[x_{0}, \infty\right)\). Thus, \(h\) is monotone increasing on this interval. It follows that \[h(x) \geq h\left(x_{0}\right)=g\left(x_{0}\right)-f\left(x_{0}\right)=0 \text { for all } x \geq x_{0} .\] Therefore, \(g(x) \geq f(x)\) for all \(x \geq x_{0}\).

Exercise \(4.3.5\).

Answer

Apply the mean value theorem twice.

Exercise \(4.3.6\).

Answer

Use proof by contradiction.

Exercise \(4.4.5\).

Answer

Suppose that \[P(x)=a_{0}+a_{1} x+\cdots+a_{n} x^{n} .\] Then apply L'Hospital's rule repeatedly.

Exercise \(4.4.6\).

Answer

We first consider the case where \(n = 1\) to get ideas for solving this problem in the general case. From the standard derivative theorems we get that the function is differentiable at any \(x \neq 0\) with \[f^{\prime}(x)=2 x^{-3} e^{-\frac{1}{x^{2}}}=\frac{2}{x^{3}} e^{-\frac{1}{x^{2}}} .\] Consider the limit \[\lim _{x \rightarrow 0} \frac{f(x)-f(0)}{x-0}=\lim _{x \rightarrow 0} \frac{e^{-\frac{1}{x^{2}}}}{x} .\] Letting \(t=1 / x\) and applying L'Hospital rule yields \[\lim _{x \rightarrow 0^{+}} \frac{e^{-\frac{1}{x^{2}}}}{x}=\lim _{t \rightarrow \infty} \frac{t}{e^{t^{2}}}=\lim _{t \rightarrow \infty} \frac{1}{2 t e^{t^{2}}}=0 .\] SImilarly, \[\lim _{x \rightarrow 0^{-}} \frac{e^{-\frac{1}{x^{2}}}}{x}=0 .\] It follows that \(f\) is differentiable on \(\mathbb{R}\) with \[f^{\prime}(x)=\left\{\begin{array}{ll}
\frac{2}{x^{3}} e^{-\frac{1}{x^{2}}}, & \text { if } x \neq 0 \text {;}\\
0, & \text { if } x=0 \text {.}
\end{array}\right.\] In a similar way, we can show that \(f\) is twice differentiable on \(\mathbb{R}\) with \[f^{\prime \prime}(x)=\left\{\begin{array}{ll}
\left(\frac{6}{x^{4}}+\frac{2}{x^{6}}\right) e^{-\frac{1}{x^{2}}}, & \text { if } x \neq 0 \text {;}\\
0, & \text { if } x=0 \text {.}
\end{array}\right.\] Based on these calculations, we predict that \(f\) is \(n\) times differentiable for every \(n \in \mathbb{N}\) with \[f^{(n)}(x)=\left\{\begin{array}{ll}
P\left(\frac{1}{x}\right) e^{-\frac{1}{x^{2}}}, & \text { if } x \neq 0 \text {;}\\
0, & \text { if } x=0 \text {,}
\end{array}\right.\] where \(P\) is a polynomial. Now we proceed to prove this conclusion by induction. The conclusion is true for \(n = 1\) as shown above. Given that the conclusion is true for some \(n \in \mathbb{N}\), for \(x \neq 0\) we have \[f^{(n+1)}(x)=-x^{-2} P^{\prime}\left(\frac{1}{x}\right)+\frac{2}{x^{3}} P\left(\frac{1}{x}\right) e^{-\frac{1}{x^{2}}}=Q\left(\frac{1}{x}\right) e^{-\frac{1}{x^{2}}} ,\] where \(Q\) is also a polynomial. It is an easy exercise to write the explicit formula of \(Q\) based on \(P\). Moreover, successive applications of l'Hôpital's rule give \[\lim _{x \rightarrow 0^{+}} \frac{f^{(n)}(x)-f^{(n)}(0)}{x-0}=\lim _{x \rightarrow 0^{+}} \frac{1}{x} P\left(\frac{1}{x}\right) e^{-\frac{1}{x^{2}}}=\lim _{t \rightarrow \infty} \frac{t P(t)}{e^{t^{2}}}=0 .\] In a similar way, we can show that \[\lim _{x \rightarrow 0^{-}} \frac{f^{(n)}(x)-f^{(n)}(0)}{x-0}=0 .\] Therefore, \(f^{(n+1)}(0)=0\). We have proved that for every \(n \in \mathbb{N}\), \(f\) is \(n\) times differentiable and, so, \(f \in C^{n}(\mathbb{R})\). Here we do not need to prove the continuity of \(f^{(n)}\) because the differentiability of \(f^{(n)}\) implies its continuity.

In a similar way, we can also show that the function \[f(x)=\left\{\begin{array}{ll}
e^{-\frac{1}{x}}, & \text { if } x>0 \text {;}\\
0, & \text { if } x \leq 0
\end{array}\right.\] is \(n\) times differentiable for every \(n \in \mathbb{N}\).

Exercise \(4.5.1\).

Answer

Let \(f(x)=e^{x}\). By Taylor's theorem, for any \(x > 0\), there exists \(c \in (0, x)\) such that \[\begin{aligned}
f(x) &=e^{x}=\sum_{k=0}^{m} \frac{f^{(k)}(0)}{k !} x^{k}+\frac{f^{(m+1)}(c)}{(m+1) !} c^{m+1} \\
&=\sum_{k=0}^{m} \frac{x^{k}}{k !}+\frac{e^{c}}{(m+1) !} c^{m+1}>\sum_{k=0}^{m} \frac{x^{k}}{k !}
\end{aligned} .\]

Exercise \(4.5.5\).

Answer

1. Observe that a simpler version of this problem can be stated as follows: If \(f\) is differentiable on \((a, b)\) and \(\bar{x} \in (a, b)\), then \[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})}{h}=\frac{f^{\prime}(\bar{x})}{1 !} .\] This conclusion follows directly from the definition of derivative.

Similarly, if \(f\) is twice differnetaible on \((a, b)\) and \(\bar{x} \in (a, b)\), then \[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})-f^{\prime}(\bar{x}) \frac{h}{1 !}}{h^{2}}=\frac{f^{\prime \prime}(\bar{x})}{2 !} .\] We can prove this by applying the L'Hospital rule to get \[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})-f^{\prime}(\bar{x}) \frac{h}{1 !}}{h^{2}}=\lim _{h \rightarrow 0} \frac{f^{\prime}(\bar{x}+h)-f^{\prime}(\bar{x})}{2 h}=\frac{f^{\prime \prime}(\bar{x})}{2 !} .\] It is now clear that we can solve part (a) by using the L'Hospital rule as follows: \[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-f(\bar{x})-f^{\prime}(\bar{x}) \frac{h}{1 !}-f^{\prime \prime}(\bar{x}) \frac{h^{2}}{2 !}}{h^{3}}=\lim _{h \rightarrow 0} \frac{f^{\prime}(\bar{x}+h)-f^{\prime}(\bar{x})-f^{\prime \prime}(\bar{x}) \frac{h}{1 !}}{3 h^{2}}=\frac{f^{\prime \prime \prime}(\bar{x})}{3 !} .\] Note that the last equality follows from the previous proof applied to the function \(f^{\prime}\).

2. With the analysis from part (a), we see that if \(f\) is \(n\) times differentiable on \((a, b)\) and \(\bar{x} \in (a, b)\), then \[\lim _{h \rightarrow 0} \frac{f(\bar{x}+h)-\sum_{k=0}^{n-1} \frac{f^{(k)}(\bar{x}) h^{k}}{k !}}{h^{n+1}}=\frac{f^{(n)}(\bar{x})}{n !} .\] This conclusion can be proved by induction. This general result can be applied to obtain the Taylor expansion with Peano's remainder in Exerciser 4.5.6.

Exercise \(4.6.3\).

Answer

We apply the definition to solve this problem. Given any \(u, v \in I\) and \(\lambda \in (0, 1)\), we have \[f(\lambda u+(1-\lambda) v) \leq \lambda f(u)+(1-\lambda) f(v)\] by the convexity of \(f\).

Since \(f(u), f(v) \in J\) and \(J\) is an interval, \(\lambda f(u)+(1-\lambda) f(v) \in J\). By the nondecreasing property and the convexity of \(\phi\). \[\phi(f(\lambda u+(1-\lambda) v)) \leq \phi(\lambda f(u)+(1-\lambda) f(v)) \leq \lambda \phi(f(u))+(1-\lambda) \phi(f(v)).\] Therefore, \(\phi \circ f\) is convex on \(I\).

The result from this problem allows us to generate convex functions. For example, consider \(f(x) = |x|\) and \(\phi(x)=x^{p}\), \(p > 1\). We have seen that \(f\) is convex on \(\mathbb{R}\). The function \(\phi\) is convex and increasing on \([0, \infty)\) which contains the range of the function \(f\). Therefore, the composition \(g(x)=|x|^{p}\), \(p > 1\), is convex on \(\mathbb{R}\). Similarly, \(h(x)=e^{x^{2}}\) is also a convex function on \(\mathbb{R}\).

Observe that in this problem, we require the nondecreasing property of \(\phi\). A natural question is whether the composition of two convex functions is convex. The answer is negative. Observe that \(f(x) = x^{2}\) and \(h(x)=e^{x^{2}}\phi(x)=|x-1|\) are convex, but \((\phi \circ f)(x)=\left|x^{2}-1\right|\) is nonconvex.

Exercise \(4.6.4\).

Answer

1. Use the obvious inequality \[(\sqrt{a}-\sqrt{b})^{2} \geq 0 .\] Alternatively, consider the function \(f(x)=-\ln (x)\), \(x \in (0, \infty)\). We can show that \(f\) is convex on \((0, \infty)\). For \(a, b \in (0, \infty)\), one has \[f\left(\frac{a+b}{2}\right) \leq \frac{f(a)+f(b)}{2} .\] This implies \[-\ln \left(\frac{a+b}{2}\right) \leq \frac{-\ln (a)-\ln (b)}{2}=-\ln (\sqrt{a b}) .\] Therefore, \[\frac{a+b}{2} \geq \sqrt{a b} .\] This inequality holds obviously when \(a = 0\) or \(b = 0\).
2. Use Theorem 4.6.3 for the function \(f(x)=-\ln (x)\) on \((0, \infty)\).

Exercise \(4.7.1\).

Answer

1. By Theorem 4.7.5, \[\partial f(x)=\left\{\begin{array}{ll}
   \{-a\}, & \text { if } x<0 \text {;}\\
   {[-a, a],} & \text { if } x=0 \text {;}\\
   \{a\}, & \text { if } x>0 \text {.}
   \end{array}\right.\]
2. By Theorem 4.7.5, \[\partial f(x)=\left\{\begin{array}{ll}
   \{-2\}, & \text { if } x<-1 \text {;}\\
   {[-2,0],} & \text { if } x=-1 \text {;}\\
   \{0\}, & \text { if } x \in(-1,1) \text {;}\\
   {[0,2],} & \text { if } x=1 \text {;}\\
   \{2\}, & \text { if } x>1 \text {.}
   \end{array}\right.\]

Exercise \(4.7.3\).

Answer

To better understand the problem, we consider some special cases. If \(n = 1\), then \(f(x)=|x-1|\). Obviously, \(f\) has an absolute minimum at \(x = 1\). If \(n = 2\), then \(f(x)=|x-1|+|x-2|\). The graphing of the function suggests that \(f\) has an absolute minimum at any \(x \i [1, 2]\). In the case where \(n = 3\), we can see that \(f\) has an absolute minimum at \(x = 2\). We then conjecture that if \(n\) is odd with \(n=2 m-1\), then \(f\) has an absolute minimum at \(x = m\). If \(n\) is even with \(n = 2m\), then \(f\) has an absolute minimum at any point \(x \in[m, m+1]\).

Let us prove the first conclusion. In this case, \[f(x)=\sum_{i=1}^{2 m-1}|x-i|=\sum_{i=1}^{2 m-1} f_{i}(x) ,\] where \(f_{i}(x)=|x-i|\). Consider \(\bar{x} = m\). Then \[\partial f_{m}(\bar{x})=[-1,1], \partial f_{i}(\bar{x})=\{1\} \text { if } i<m, \partial f_{i}(\bar{x})=\{-1\} \text { if } i>m .\] The subdifferential sum rule yields \(\partial f(\bar{x})=[-1,1]\) which contains \(0\). Thus, \(f\) has an absolute minimum at \(\bar{x}\). If \(\bar{x} > m\), we can see that \(\partial f(\bar{x}) \subset(0, \infty)\), which does not contain \(0\). Similarly, if \(\bar{x} < m\), then \(\partial f(\bar{x}) \subset(-\infty, 0)\). Therefore, \(f\) has an absolute minimum at the only point \(\bar{x} = m\).

The case where \(n\) is even can be treated similarly.

Exercise \(4.7.5\).

Answer

Fix \(a, b \in \mathbb{R}\) with \(a < b\). By Theorem 4.7.9, there exists \(c \in (a, b)\) such that \[\frac{f(b)-f(a)}{b-a} \in \partial f(c) \subset[0, \infty) .\] This implies \(f(b)-f(a) \geq 0\) and, hence, \(f(b) \geq f(a)\). Therefore, \(f\) is monotone increasing on \(\mathbb{R}\).