1.6: Riemann Extension Theorem, Zero Sets, and Injective Maps
- Page ID
- 74227
In one dimension if a function is holomorphic in \(U \setminus \{ p \}\) and locally bounded\(^{1}\) in \(U\), in particular bounded near \(p\), then the function extends holomorphically to \(U\) (see Proposition B.22 (i)). In several variables the same theorem holds, and the analogue of a single point is the zero set of a holomorphic function.
Let \(U \subset \mathbb{C}^n\) be a domain, \(g \in \mathcal{O}(U)\), and \(g\) is not identically zero. Let \(N = g^{-1}(0)\) be the zero set of \(g\). If \(f \in \mathcal{O}(U \setminus N)\) is locally bounded in \(U\), then there exists a unique \(F \in \mathcal{O}(U)\) such that \(F|_{U \setminus N} = f\).
The proof is an application of the Riemann extension theorem from one dimension.
- Proof
-
Take any \(p \in N\), and let \(L\) be a complex line through \(p\). That is, \(L\) is an image of an affine mapping \(\varphi \colon \mathbb{C} \to \mathbb{C}^n\) defined by \(\varphi(\xi) = a\xi + p\), for a vector \(a \in \mathbb{C}^n\). The composition \(g \circ \varphi\) is a holomorphic function of one variable, and it is either identically zero, or the zero at \(\xi=0\) is isolated. The function \(g\) is not identically zero in any neighborhood of \(p\). So there is some line \(L\) such that \(g \circ \varphi\) is not identically zero, or in other words, \(p\) is an isolated point of \(L \cap N\).
Write \(z' = (z_1,\ldots,z_{n-1})\) and \(z=(z',z_n)\). Without loss of generality \(p = 0\), and \(L\) is the line obtained by \(z' = 0\). So \(g \circ \varphi\) is \(\xi \mapsto g(0,\xi)\). There is some small \(r > 0\) such that \(g\) is nonzero on the set given by \(|z_n| = r\) and \(z' = 0\). By continuity, \(g\) is nonzero on the set given by \(|z_n| = r\) and \(||z'|| <\epsilon\) for some \(\epsilon >0\). In particular, for any fixed small \(s \in \mathbb{C}^{n-1}\), with \(||s|| < \epsilon\), setting \(z' = s\), the zeros of \(\xi \mapsto g(s,\xi)\) are isolated. See Figure \(\PageIndex{1}\).
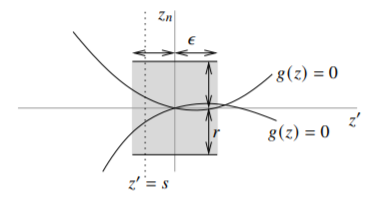
Figure \(\PageIndex{1}\)
For \(||z'|| < \epsilon\) and \(|z_n| < r\), write \[F(z',z_n) = \frac{1}{2\pi i} \int_{|\xi|=r} \frac{f(z',\xi)}{\xi-z_n} \,d\xi .\] The function \(\xi \to f(z',\xi)\) extends holomorphically to the entire disc of radius \(r\) by the Riemann extension from one dimension. By Cauchy integral formula, \(F\) is equal to \(f\) at the points where they are both defined. By differentiating under the integral, the function \(F\) is holomorphic in all variables.
In a neighborhood of each point of \(N\), \(f\) extends to a continuous (holomorphic in fact) function. A continuous extension of \(f\) must be unique on the closure of \(U \setminus N\) in the subspace topology, \(\overline{(U \setminus N)} \cap U\). The set \(N\) has empty interior, so \(\overline{(U \setminus N)} \cap U = U\). Hence, \(F\) is the unique continuous extension of \(f\) to \(U\).
Let \(F\) be a meromorphic function on an open set \(U \subset \mathbb{C}^n\). Show that if \(p \in U\) is a pole (near \(p\), \(F=\frac{f}{g}\), and \(F\) does not extend through \(p\)), then there exists a sequence \(\{ p_k \}\) converging to \(p\) such that \(F(p_k) \to \infty\). Namely, \(F\) is unbounded near \(p\).
The set of zeros of a holomorphic function has a nice structure at most points.
Let \(U \subset \mathbb{C}^n\) be a domain and \(f \in \mathcal{O}(U)\) and \(f\) is not identically zero. Let \(N = f^{-1}(0)\). Then there exists a open and dense (subspace topology) subset \(N_{\mathit{reg}} \subset N\) such that near each \(p \in N_{\mathit{reg}}\), after possibly reordering variables, \(N\) can be locally written as \[z_n = g(z_1,\ldots,z_{n-1}) \] for a holomorphic function \(g\).
- Proof
-
If \(N\) is locally a graph at \(p\), then it is a graph for every point of \(N\) near \(p\). So \(N_{\mathit{reg}}\) is open. If for every point \(p_0 \in N\) and every neighborhood \(W\) of \(p_0\), we show that \(N \cap W\) has a regular point, then \(N_{\mathit{reg}}\) is dense. Replacing \(N\) with \(N \cap W\), it thus suffices to show \(N_{\mathit{reg}}\) is nonempty.
Since \(f\) is not identically zero, then not all derivatives (of arbitrary order) of \(f\) vanish identically on \(N\). If some first order derivative of \(f\) does not vanish identically on \(N\), let \(h=f\). Otherwise, suppose \(k\) is such that a derivative of \(f\) of order \(k\) does not vanish identically on \(N\), and all derivatives of \(f\) order less than \(k\) vanish identically on \(N\). Let \(h\) be one of the derivatives of order \(k-1\). We obtain a function \(h \colon U \to \mathbb{C}\), holomorphic, vanishing on \(N\), and such that without loss of generality the \(z_n\) derivative does not vanish identically on \(N\). Then there is some point \(p \in N\) such that \(\frac{\partial h}{\partial z_n}(p) \not= 0\). We apply the implicit function theorem at \(p\) to find \(g\) such that \[h\bigr(z_1,\ldots,z_{n-1},g(z_1,\ldots,z_{n-1})\bigr) = 0 ,\] and \(z_n = g(z_1,\ldots,z_{n-1})\) is the unique solution to \(h=0\) near \(p\).
The zero set of \(h\) contains \(N\), the zero set of \(f\). We must show equality near \(p\). That is, we need to show that near \(p\), every zero of \(h\) is also a zero of \(f\). Write \(p = (p',p_n)\). Then the function \[\xi \mapsto f(p',\xi)\] has an isolated zero in a small disc \(\Delta\) around \(p_n\) and is nonzero on the circle \(\partial \Delta\). By Rouché’s theorem, \(\xi \mapsto f(z',\xi)\) must have a zero for all \(z'\) sufficiently close to \(p'\) (close enough to make \(|f(q',\xi)-f(z',\xi)| < |f(q',\xi)|\) for all \(\xi \in \partial \Delta\)). Since \(g(z')\) is the unique solution \(z_n\) to \(h(z',z_n) = 0\) near \(p\) and the zero set of \(f\) is contained in the zero set of \(h\), we are done.
The zero set \(N\) of a holomorphic function is a so-called subvariety or an analytic set although the general definition of a subvariety is more complicated, and includes more sets. See Chapter 6. Points where \(N\) is a graph of a holomorphic mapping are called regular points, and we write them as \(N_{\mathit{reg}}\) as above. In particular, since \(N\) is a graph of a single holomorphic function, they are called regular points of (complex) dimension \(n-1\), or (complex) codimension 1. The set of regular points is what is called an \((n-1)\)-dimensional complex submanifold. It is also a real submanifold of real dimension \(2n-2\). The points on a subvariety that are not regular are called singular points.
For \(U = \mathbb{C}^2\), let \(f(z) = z_1^2-z_2^2\) and consider \(X = f^{-1}(0)\). As \(\nabla f = (2z_1,2z_2)\), outside of the origin, we can solve for \(z_1\) or \(z_2\) and so all points of \(X \setminus 0\) are regular. In fact, \(z_1 = z_2\) and \(z_1 = -z_2\) are the two possibilities. In no neighborhood of the origin, however, is there a way to solve for either \(z_1\) or \(z_2\), since you always get two possible solutions: If you could solve \(z_1 = g(z_2)\), then both \(z_2 = g(z_2)\) and \(-z_2 = g(z_2)\) must be true, a contradiction for any nonzero \(z_2\). Similarly, we cannot solve for \(z_1\). So the origin is a singular point.
To see that you may have need to use derivatives of the function, notice that the function \(\varphi(z) = {(z_1^2-z_2^2)}^2\) has the same zero set \(X\), but both \(\frac{\partial \varphi}{\partial z_1}\) and \(\frac{\partial \varphi}{\partial z_2}\) vanish on \(X\). Using \(h= \frac{\partial \varphi}{\partial z_1}\) or \(h= \frac{\partial \varphi}{\partial z_2}\) in the proof will work.
It may be also good to consider a function such as \(f(z) = z_1^2z_2\) to see that we do not always get the entire set of regular functions with one neighborhood \(W\). The zero set is where \(z_1=0\) or where \(z_2=0\), and all points except the origin are regular. We use \(h=f\) to show that points outside the origin where \(z_2=0\) are regular. To show that points outside the origin where \(z_1=0\) are regular, we must restrict to some neighborhood \(W\) of those points and use \(h = \frac{\partial f}{\partial z_1}\).
The theorem is not true in the nonholomorphic setting. The set where \(x_1^2 + x_2^2 = 0\) in \(\mathbb{R}^2\) is only the origin, clearly not a graph of any function of one variable. The first part of the theorem works, but the \(h\) you find is either \(2x_1\) or \(2x_2\), and its zero set is too big.
Find all the regular points of the subvariety \(X = \bigl\{ z \in \mathbb{C}^2 : z_1^2 = z_2^3 \bigr\}\). Hint: The trick is showing that you’ve found all of them.
Suppose \(U \subset \mathbb{C}^n\) is a domain and \(f \in \mathcal{O}(U)\). Show that the complement of the zero set, \(U \setminus f^{-1}(0)\), is connected.
Let us now prove that a one-to-one holomorphic mapping is biholomorphic, a result definitely not true in the smooth setting: \(x \mapsto x^3\) is smooth, one-to-one, onto map of \(\mathbb{R}\) to \(\mathbb{R}\), but the inverse is not differentiable.
Suppose \(U \subset \mathbb{C}^n\) is an open set and \(f \colon U \to \mathbb{C}^n\) is holomorphic and one-to-one. Then the Jacobian determinant is never equal to zero on \(U\).
In particular, if a holomorphic map \(f \colon U \to V\) is one-to-one and onto for two open sets \(U,V \subset \mathbb{C}^n\), then \(f\) is biholomorphic.
- Proof
-
We proceed by induction. We know the theorem for \(n=1\). Suppose \(n > 1\) and suppose we know the theorem is true for dimension \(n-1\).
Suppose for contradiction that \(J_f = 0\) somewhere. First suppose that \(J_f\) is not identically zero. Find a regular point \(q\) on the zero set of \(J_f\). Write the zero set of \(J_f\) near \(q\) as \[z_n = g(z_1,\ldots,z_{n-1})\] for some holomorphic \(g\). If we prove the theorem near \(q\), we are done. Without loss of generality assume \(q=0\). The biholomorphic (near the origin) map \[\Psi(z_1,\ldots,z_n) = \bigl(z_1,z_2,\ldots,z_{n-1},z_n-g(z_1,\ldots,z_{n-1}) \bigr)\] takes the zero set of \(J_f\) to the set given by \(z_n=0\). By considering \(f \circ \Psi^{-1}\) instead of \(f\), we may assume that \(J_f = 0\) on the set given by \(z_n=0\). We may also assume that \(f(0) = 0\).
If \(J_f\) vanishes identically, then there is no need to do anything other than a translation. In either case, we may assume that \(0 \in U\), \(f(0)=0\), and \(J_f = 0\) when \(z_n=0\).
We wish to show that all the derivatives of \(f\) in the \(z_1,\ldots,z_{n-1}\) variables vanish whenever \(z_n = 0\). This would clearly contradict \(f\) being one-to-one, as \(f(z_1,\ldots,z_{n-1},0)\) would be constant. So for any point on \(z_n=0\) we consider one of the components of \(f\) and one of the derivatives of that component. Without loss of generality, suppose the point is 0, and for contradiction suppose \(\frac{\partial f_1}{\partial z_1}(0) \not= 0\). The map \[G(z_1,\ldots,z_n) = \bigl(f_1(z),z_2,\ldots,z_n\bigr)\] is biholomorphic on a small neighborhood of the origin. The function \(f \circ G^{-1}\) is holomorphic and one-to-one on a small neighborhood. By the definition of \(G\), \[f \circ G^{-1} (w_1,\ldots,w_n) = \bigl(w_1,h(w)\bigr) ,\] where \(h\) is a holomorphic mapping taking a neighborhood of the origin in \(\mathbb{C}^n\) to \(\mathbb{C}^{n-1}\). The mapping \[\varphi(w_2,\ldots,w_n) = h(0,w_2,\ldots,w_n)\] is a one-to-one holomorphic mapping of a neighborhood of the origin in \(\mathbb{C}^{n-1}\) to \(\mathbb{C}^{n-1}\). By the induction hypothesis, the Jacobian determinant of \(\varphi\) is nowhere zero.
If we differentiate \(f \circ G^{-1}\), we notice \(D(f \circ G^{-1}) = Df \circ D(G^{-1})\). So at the origin \[\det D(f \circ G^{-1}) = \bigl(\det Df\bigr) \bigl(\det D(G^{-1})\bigr) = 0.\] We obtain a contradiction, as at the origin \[\det D(f \circ G^{-1}) = \det D\varphi \not= 0 . \]
The function \(f\) is locally biholomorphic, in particular \(f^{-1}\) is holomorphic, on the set where the Jacobian determinant \[J_f(z) = \det Df(z) = \det \left[ \frac{\partial f_j}{\partial z_k}(z) \right]_{jk}\] is not zero. This follows from the inverse function theorem, which is just a special case of the implicit function theorem. The trick is to show that \(J_f\) happens to be nonzero everywhere.
In one complex dimension, every holomorphic function \(f\) can, in the proper local holomorphic coordinates (and up to adding a constant), be written as \(z^d\) for \(d=0,1,2,\ldots\): Near a \(z_0 \in \mathbb{C}\), there exists a constant \(c\) and a local biholomorphic \(g\) with \(g(z_0) = 0\) such that \(f(z) = c + {\bigl( g(z) \bigr)}^d\). Such a simple result does not hold in several variables in general, but if the mapping is locally one-to-one, then the present theorem says that such a mapping can be locally written as the identity.
The theorem is no longer true if the domain and range dimensions of the mapping are not equal.
Take the subvariety \(X = \bigl\{ z \in \mathbb{C}^2 : z_1^2 = z_2^3 \bigr\}\). Find a one-to-one holomorphic mapping \(f \colon \mathbb{C} \to X\). Then note that the derivative of \(f\) vanishes at a certain point. So Theorem \(\PageIndex{3}\) has no analogue when the domain and range have different dimension.
Find a continuous function \(f \colon \mathbb{R} \to \mathbb{R}^2\) that is one-to-one but such that the inverse \(f^{-1} \colon f(\mathbb{R}) \to \mathbb{R}\) is not continuous.
This is an appropriate place to state a well-known and as yet unsolved conjecture (and most likely ridiculously hard to solve): the Jacobian conjecture. This conjecture is a converse to the theorem above in a special case: Suppose \(F \colon \mathbb{C}^n \to \mathbb{C}^n\) is a polynomial map (each component is a polynomial) and the Jacobian derivative \(J_F\) is never zero, then \(F\) is invertible with a polynomial inverse. Clearly \(F\) would be locally one-to-one, but proving (or disproving) the existence of a global polynomial inverse is the content of the conjecture.
Prove the Jacobian conjecture for \(n=1\). That is, prove that if \(F \colon \mathbb{C} \to \mathbb{C}\) is a polynomial such that \(F'\) is never zero, then \(F\) has an inverse, which is a polynomial.
Let \(F \colon \mathbb{C}^n \to \mathbb{C}^n\) be an injective polynomial map. Prove \(J_F\) is a nonzero constant.
Prove that the Jacobian conjecture is false if “polynomial” is replaced with “entire holomorphic,” even for \(n=1\).
Prove that if a holomorphic \(f \colon \mathbb{C} \to \mathbb{C}\) is injective, then it is onto, and therefore \(f(z) = az + b\) for \(a \not= 0\).
We remark that while every injective holomorphic map of \(f \colon \mathbb{C} \to \mathbb{C}\) is onto, the same is not true in higher dimensions. In \(\mathbb{C}^n\), \(n \geq 2\), there exist so-called Fatou–Bieberbach domains, that is, proper subsets of \(\mathbb{C}^n\) that are biholomorphic to \(\mathbb{C}^n\).
Footnotes
[1] \(f \colon U \setminus X \to \mathbb{C}\) is locally bounded in \(U\) if for every \(p \in U\), there is a neighborhood \(W\) of \(p\) such that \(f\) is bounded on \(W \cap (U \setminus X)\).


