4.2: Simple Case of The ∂-Problem
- Page ID
- 74239
For a smooth function \(\psi\), consider the exterior derivative in terms of \(z\) and \(\bar{z}\), \[d \psi = \frac{\partial \psi}{\partial z_1} dz_1 + \cdots + \frac{\partial \psi}{\partial z_n} dz_n + \frac{\partial \psi}{\partial \bar{z}_1} d\bar{z}_1 + \cdots + \frac{\partial \psi}{\partial \bar{z}_n} d\bar{z}_n .\] Let us give a name to the two parts of the derivative: \[\partial \psi \overset{\text{def}}{=} \frac{\partial \psi}{\partial z_1} dz_1 + \cdots + \frac{\partial \psi}{\partial z_n} dz_n, \qquad \bar{\partial} \psi \overset{\text{def}}{=} \frac{\partial \psi}{\partial \bar{z}_1} d\bar{z}_1 + \cdots + \frac{\partial \psi}{\partial \bar{z}_n} d\bar{z}_n .\] Then \(d \psi = \partial \psi + \bar{\partial} \psi\). Notice \(\psi\) is holomorphic if and only if \(\bar{\partial} \psi = 0\).
The so-called inhomogeneous \(\bar{\partial}\)-problem (\(\bar{\partial}\) is pronounced “dee bar”) is to solve the equation \[\bar{\partial} \psi = g ,\] for \(\psi\), given a one-form \[g = g_1 d\bar{z}_1 + \cdots + g_n d\bar{z}_n .\] Such a \(g\) is called a (0,1)-form. The fact that the partial derivatives of \(\psi\) commute, forces certain compatibility conditions on \(g\) for us to have any hope of getting a solution (see below).
Find an explicit example of a \(g\) in \(\mathbb{C}^2\) such that no corresponding \(\psi\) exists.
On any open set where \(g = 0\), \(\psi\) is holomorphic. So for a general \(g\), what we are doing is finding a function that is not holomorphic in a specific way.
Suppose \(g\) is a \((0,1)\)-form on \(\mathbb{C}^n\), \(n \geq 2\), given by \[g = g_1 d\bar{z}_1 + \cdots + g_n d\bar{z}_n ,\] where \(g_j \colon \mathbb{C}^n \to \mathbb{C}\) are compactly supported smooth functions satisfying the compatibility conditions \[\label{eq:1} \frac{\partial g_k}{\partial \bar{z}_\ell} = \frac{\partial g_\ell}{\partial \bar{z}_k} \qquad \text{for all $k,\ell = 1,2,\ldots,n$.}\] Then there exists a unique compactly supported smooth function \(\psi \colon \mathbb{C}^n \to \mathbb{C}\) such that \[\bar{\partial} \psi = g .\]
The compatibility conditions on \(g\) are necessary, but the compactness is not. Without compactness, the boundary of the set where the equation lives would come into play. Let us not worry about this, and prove that this simple compactly supported version always has a solution. The compactly supported solution is unique: Given any holomorphic \(f\), \(\bar{\partial}(\psi+f) = g\). But since the difference of any two solutions \(\psi_1\) and \(\psi_2\) is holomorphic, and the only holomorphic compactly supported function is 0, then the compactly supported solution \(\psi\) is unique.
- Proof
-
Really there are \(n\) smooth functions, \(g_1,\ldots,g_n\), so the equation \(\bar{\partial} \psi = g\) consists of the \(n\) equations \[\frac{\partial \psi}{\partial \bar{z}_k} = g_k ,\] where the functions \(g_k\) satisfy the compatibility conditions \(\eqref{eq:1}\).
We claim that the following is an explicit solution: \[\begin{align}\begin{aligned} \psi(z) & = \frac{1}{2\pi i} \int_{\mathbb{C}} \frac{ g_1(\zeta,z_2,\ldots,z_n) }{\zeta - z_1} d\zeta \wedge d\bar{\zeta} \\ & = \frac{1}{2\pi i} \int_{\mathbb{C}} \frac{ g_1(\zeta+z_1,z_2,\ldots,z_n) }{\zeta} d\zeta \wedge d\bar{\zeta} . \end{aligned}\end{align}\] To show that the singularity does not matter for integrability is the same idea as for the generalized Cauchy formula.
Let us check that \(\psi\) is the solution. We use the generalized Cauchy formula on the \(z_1\) variable. Take \(R\) large enough so that \(g_j(\zeta,z_2,\ldots,z_n)\) is zero when \(|\zeta|\geq R\) for all \(j\). For every \(j\), \[\begin{align}\begin{aligned} g_j(z_1,\ldots,z_n) & = \frac{1}{2\pi i} \int_{|\zeta|=R} \frac{g_j(\zeta,z_2,\ldots,z_n)}{\zeta-z_1} d \zeta + \frac{1}{2\pi i} \int_{|\zeta| \leq R} \frac{\frac{\partial g_j}{\partial \bar{z}_1}(\zeta,z_2,\ldots,z_n)}{\zeta-z_1} d\zeta \wedge d\bar{\zeta} \\ & = \frac{1}{2\pi i} \int_{\mathbb{C}} \frac{\frac{\partial g_j}{\partial \bar{z}_1}(\zeta,z_2,\ldots,z_n)}{\zeta-z_1} d\zeta \wedge d\bar{\zeta} . \end{aligned}\end{align}\]
Using the second form of the definition of \(\psi\), the compatibility conditions \(\eqref{eq:1}\), and the computation above we get \[\begin{align}\begin{aligned} \frac{\partial\psi}{\partial \bar{z}_j}(z) & = \frac{1}{2\pi i} \int_{\mathbb{C}} \frac{ \frac{\partial g_1}{\partial \bar{z}_j}(\zeta+z_1,z_2,\ldots,z_n) }{\zeta} d\zeta \wedge d\bar{\zeta} \\ & = \frac{1}{2\pi i} \int_{\mathbb{C}} \frac{ \frac{\partial g_j}{\partial \bar{z}_1}(\zeta+z_1,z_2,\ldots,z_n) }{\zeta} d\zeta \wedge d\bar{\zeta} \\ & = \frac{1}{2\pi i} \int_{\mathbb{C}} \frac{ \frac{\partial g_j}{\partial \bar{z}_1}(z_1,z_2,\ldots,z_n) }{\zeta-z_1} d\zeta \wedge d\bar{\zeta} = g_j(z) . \end{aligned}\end{align}\]
Show that we were allowed to differentiate under the integral in the computation above.
That \(\psi\) has compact support follows because \(g_1\) has compact support together with the identity theorem. In particular, \(\psi\) is holomorphic for large \(z\) since \(\bar{\partial} \psi = g = 0\) when \(z\) is large. When at least one of \(z_2,\ldots,z_n\) is large, then \(\psi\) is identically zero simply from its definition. See Figure \(\PageIndex{1}\).
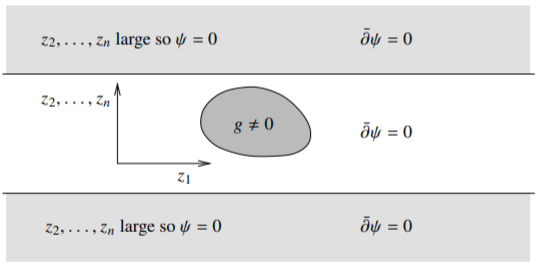
Figure \(\PageIndex{1}\)
As \(\bar{\partial} \psi = 0\) on the light gray and white areas in the diagram, \(\psi\) is holomorphic there. As \(\psi\) is zero on the light gray region, it is zero also on the white region by the identity theorem. That is, \(\psi\) is zero on the unbounded component of the set where \(g=0\), and so \(\psi\) has compact support.
The first part of the proof still works when \(n=1\), we get a solution \(\psi\). However, the last bit of the proof does not work in one dimension, so \(\psi\) does not have compact support.
- Show that if \(g\) is supported in \(K \subset \subset \mathbb{C}^n\), \(n \geq 2\), then \(\psi\) is supported in the complement of the unbounded component of \(\mathbb{C}^n \setminus K\). In particular, show that if \(K\) is the support of \(g\) and \(\mathbb{C}^n \setminus K\) is connected, then the support of \(\psi\) is \(K\).
- Find an explicit example where the support of \(\psi\) is strictly larger than the support of \(g\).
Find an example of a smooth function \(g \colon \mathbb{C} \to \mathbb{C}\) with compact support, such that no solution \(\psi \colon \mathbb{C} \to \mathbb{C}\) to \(\frac{\partial \psi}{\partial \bar{z}} = g\) (at least one of which always exists) is of compact support.


