7.3: Distance
( \newcommand{\kernel}{\mathrm{null}\,}\)
The properties of the network that we have examined so far primarily deal with adjacencies - the direct connections from one actor to the next. But the way that people are embedded in networks is more complex than this. Two persons, call them A and B, might each have five friends. But suppose that none of person A's friends have any friends except A. Person B's five friends, in contrast, each have five friends. The information available to B and B's potential for influence is far greater than A's. That is, sometimes being a "friend of a friend" may be quite consequential.
To capture this aspect of how individuals are embedded in networks, one main approach is to examine the distance that an actor is from others. If two actors are adjacent, the distance between them is one (that is, it takes one step for a signal to go from the source to the receiver). If A tells B, and B tells C (and A does not tell C), then actors A and C are at a distance of two. How many actors are at various distances from each actor can be important for understanding the differences among actors in the constraints and opportunities they have as a result of their position. Sometimes we are also interested in how many ways there are to connect between two actors, at a given distance. That is, can actor A reach actor B in more than one way? Sometimes multiple connections may indicate a stronger connection between two actors than a single connection.
The distances among actors in a network may be an important macro-characteristic of the network as a whole. Where distances are great, it may take a long time for information to diffuse across a population. It may also be that some actors are quite unaware of, and influenced by others - even if they are technically reachable, the costs may be too high to conduct exchanges. The variability across the actors in the distances that they have from other actors may be a basis for differentiation and even stratification. Those actors who are closer to more others may be able to exert more power than those who are more distant. We will have a good deal more to say about this aspect of variability in actor distances in the next chapter.
For the moment, we need to learn a bit of jargon that is used to describe the distances between actors: walks, paths, semi-paths, etc. Using these basic definitions, we can then develop some more powerful ways of describing various aspects of the distances among actors in a network.
Walks etc.
To describe the distances between actors in a network with precision, we need some terminology. And, as it turns out, whether we are talking about a simple graph or a directed graph makes a good bit of difference. If A and B are adjacent in a simple graph, they have a distance of one. In a direct graph, however, A can be adjacent to B while B is not adjacent to A - the distance from A to B is one, but there is no distance from B to A. Because of this difference, we need slightly different terms to describe distances between actors in graphs and digraphs.
Simple graphs: The most general form of connection between two actors in a graph is called a walk. A walk is a sequence of actors and relations that begins and ends with actors. A closed walk is one where the beginning and end point of the walk are the same actor. Walks are unrestricted. A walk can involve the same actor or the same relation multiple times. A cycle is a specially restricted walk that is often used in algorithms examining the neighborhoods (the points adjacent) of actors. A cycle is a closed walk of 3 or more actors, all of whom are distinct, except for the origin/destination actor. The length of a walk is simply the number of relations contained in it. For example, consider this graph in Figure 7.10.
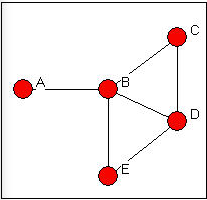
Figure 7.10: Walks in a simple graph
There are many walks in a graph (actually, an infinite number if we are willing to include walks of any length - though, usually, we restrict our attention to fairly small lengths). To illustrate just a few, begin at actor A and go to actor C. There is one walk of length 2 (A,B,C). There is one walk of length three (A,B,D,C). There are several walks of length four (A,B,E,D,C; A,B,D,B,C; A,B,E,B,C). Because these are unrestricted, the same actors and relations can be used more than once in a given walk. There are no cycles beginning and ending with A. There are some beginning and ending with actor B (B,D,C,B; B,E,D,B; B,C,D,E,B).
It is usually more useful to restrict our notion of what constitutes a connection somewhat. One possibility is to restrict the count only walks that do not re-use relations. A trail between two actors is any walk that includes a given relation no more than once (the same other actors, however, can be part of a trail multiple times. The length of a trail is the number of relations in it. All trails are walks, but not all walks are trails. If the trail begins and ends with the same actor, it is called a closed trail. In our example above, there are a number of trails from A to C. Excluded are tracings like A,B,D,B,C (which is a walk, but is not a trail because the relation BD is used more than once).
Perhaps the most useful definition of a connection between two actors (or between an actor and themselves) is a path. A path is a walk in which each other actor and each other relation in the graph may be used at most one time. The single exception to this is a closed path, which begins and ends with the same actor. All paths are trails and walks, but all walks and all trails are not paths. In our example, there are a limited number of paths connecting A and C: A,B,C; A,B,D,C; A,B,E,D,C.
Directed graphs: Walks, trails, and paths can also be defined for directed graphs. But there are two flavors of each, depending on whether we want to take direction into account or not. Semi-walks, semi-trails, and semi-paths are the same as for undirected data. In defining these distances, the directionality of connections is simply ignored (that is, arcs - or directed ties are treated as though they were edges - undirected ties). As always, the length of these distances is the number of relations in the walk, trail, or path.
If we do want to pay attention to the directionality of the connections we can define walks, trails, and paths in the same way as before, but with the restriction that we may not "change direction" as we move across relations from actor to actor. Consider the directed graph in Figure 7.11.
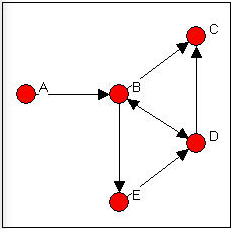
Figure 7.11: Walks in a directed graph
In this directed graph, there are a number of walks from A to C. However, there are no walks from C (or anywhere else) to A. Some of these walks from A to C are also trails (e.g. A,B,E,D,B,C). There are, however, only three paths from A to C. One path is length 2 (A,B,C); one is length three (A,B,D,C); one is length four (A,B,E,D,C).
The various kinds of connections (walks, trails, paths) provide use with a number of different ways of thinking about the distances between actors. The main reason that social network analysts are concerned with these distances is that they provide a way of thinking about the strength of ties or relations. Actors that are connected at short lengths or distances may have stronger ties. Their connection may also be less subject to disruption, and hence more stable and reliable.
The numbers of walks of a given length between all pairs of actors can be found by raising the matrix to that power. A convenient method for accomplishing this is to use Tools>Matrix Algebra, and to specify an expression like out=prod(X1,X1). This produces the square of the matrix X1, and stores it as the dataset "out". A more detailed discussion of this idea can be found in the earlier chapter on representing networks as matrices. This matrix could then be added to X1 to show the number of walks between any two actors of length two or less.
Let's look briefly at the distances between pairs of actors in the Knoke data on directed information flows. Counts of the numbers of paths of various lengths are shown in Figure 7.12.

Figure 7.12: Numbers of walks in Knoke information network
The inventory of the total connections among actors is primarily useful for getting a sense of how "close" each pair is, and for getting a sense of how closely coupled the entire system is. Here, we can see that using only connections of two steps (e.g. "A friend of a friend"), there is a great deal of connection in the graph overall; we also see that there are sharp differences among actors in their degree of connectedness, and who they are connected to. These differences can be used to understand how information moves in the network, which actors are likely to be influential on one another, and a number of other important properties.
Geodesic Distance, Eccentricity, and Diameter
One particular definition of the distance between actors in a network is used by most algorithms to define more complex properties of individual's positions and the structure of the network as a whole. This quantity is the geodesic distance. For both directed and undirected data, the geodesic distance is the number of relations in the shortest possible walk from one actor to another (or, from an actor to themselves, if we care, which we usually do not).
The geodesic distance is widely used in network analysis. There may be connections between two actors in a network. If we consider how the relation between two actors may provide each with opportunity and constraint, it may well be the case that not all of these ties matter. For example, suppose that I am trying to send a message to Sue: Since I know her email address, I can send it directly (a path of length 1). I also know Donna, and I know that Donna has Sue's email address. I could send my message for Sue to Donna, and ask her to forward it. This would be a path of length two. Confronted with this choice, I am likely to choose the geodesic path (i.e. directly to Sue) because it is less trouble and faster, and because it does not depend on Donna. That is, the geodesic path (or paths, as there can be more than one) is often the "optimal" or most "efficient" connection between two actors. Many algorithms in network analysis assume that actors will use the geodesic path when alternatives are available.
Using UCINET, we can easily locate the lengths of the geodesic paths in our directed data on information exchanges. Here is the dialog box for Network>Cohesion>Distance.
Figure 7.13: Network>Cohesion>Distance dialog
The Knoke information exchange data are binary (organization A sends information to organization B, or it doesn't). That is, the pattern is summarized by an adjacency matrix. For binary data, the geodesic distance between two actors is the count of the number of links in the shortest path between them.
It is also possible to define the distance between two actors where the links are valued. That is, where we have a measure of the strength of ties, the opportunity costs of ties, or the probability of a tie. Network>Cohesion>Distance can calculate distance (and nearness) for valued data, as well (select the appropriate "type of data").
Where we have measures of the strengths of ties (e.g. the dollar volume of trade between two nations), the "distance" between two actors is defined as the strength of the weakest path between them. If A sends 6 units to B, and B sends 4 units to C, the "strength" of the path from A to C (assuming A to B to C is the shortest path) is 4.
Where we have a measure of the probability that a link will be used, the "distance" between two actors is defined as the product along the pathway - as in path analysis in statistics.
The Nearness Transformation and Attenuation Factor parts of the dialog allow the rescaling ot distances into nearnesses. For many analyses, we may be interested in thinking about the connections among actors in terms of how close or similar they are, rather than how distant. There are a number of ways that this may be done.
The multiplicative nearness transformation divides the distance by the largest possible distance between two actors. For example, if we had 7 nodes, the maximum possible distance for adjacency data would be 6. This method gives a measure of the distance as a percentage of the theoretical maximum for a given graph.
The additive nearness transformation subtracts the actual distance between two actors from the number of nodes. It is similar to the multiplicative scaling, but yields a value as the nearness measure, rather than a proportion.
The linear nearness transformation rescales distance by reversing the scale (i.e. the closest becomes the most distant, the most distant becomes the nearest) and re-scoring to make the scale range from zero (closest pair of nodes) to one (most distant pair of nodes).
The exponential decay method turns distance into nearness by weighting the links in the pathway with decreasing values as they fall farther away from ego. With an attenuation factor of 0.5, for example, a path from A to B to C would result in a distance of 1.5.
The frequency decay method is defined as 1 minus the proportion of other actors who are as close or closer to the target as ego is. The idea (Ron Burt's) is that if there are many other actors closer to the target you are trying to reach than yourself, you are effectively "more distant".
In our example, we are using simple directed adjacencies, and the results (Figure 7.14) are quite straightforward.
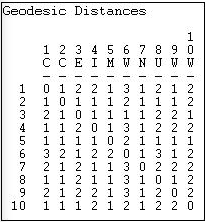
Figure 7.14: Geodesic distances for Knoke information exchange
Because the network is moderately dense, the geodesic distances are generally small. This suggests that information may travel pretty quickly in this network. Also note that there is a geodesic distance for each x,y and y,x pair - that is, the graph is fully connected, and all actors are "reachable" from all others (that is, there exists a path of some length from each actor to each other actor). When a network is not fully connected, we cannot exactly define the geodesic distances among all pairs. The standard approach in such cases is to treat the geodesic distance between unconnected actors as a length greater than that of any real distance in the data. For each actor, we could calculate the mean and standard deviation of their geodesic distances to describe their closeness to all other actors. For each actor, that actor's largest geodesic distance is called the eccentricity - a measure of how far an actor is from the furthest other.
Because the current network is fully connected, a message that starts anywhere will eventually reach everyone. Although the computer has not calculated it, we might want to calculate the mean (or median) geodesic distance, and the standard deviation in geodesic distances for the matrix, and for each actor row-wise and column-wise. This would tell us how far each actor is from each other as a source of information for the other; and how far each actor is from each other who may be trying to influence them. It also tells us which actors' behavior (in this case, whether they've heard something or not) is most predictable and least predictable.
In looking at the whole network, we see that it is connected, and that the average geodesic distance among actors is quite small. This suggests a system in which information is likely to reach everyone, and to do so fairly quickly. To get another notion of the size of a network, we might think about its diameter. The diameter of a network is the largest possible geodesic distance in the (connected) network. In the current case, no actor is more than three steps from any other - a very "compact" network. The diameter of a network tells us how "big" it is, in one sense (that is, how many steps are necessary to get from one side of it to the other). The diameter is also a useful quantity in that it can be used to set an upper bound on the lengths of connections that we study. Many researchers limit their explorations of the connections among actors to involve connections that are no longer than the diameter of the network.
Sometimes the redundancy of connection is an important feature of a network structure. If there are many efficient paths connecting two actors, the odds are improved that a signal will get from one to the other. One index of this is a count of the number of geodesic paths between each pair of actors. Of course, if two actors are adjacent, there can only be one such path. The number of geodesic paths can be calculated with Network>Cohesion>No. of Geodesics, as in Figure 7.15.
Figure 7.15: Dialog for Network>Cohesion>No. of Geodesics
The results are shown in Figure 7.16.

Figure 7.16: Number of geodesic paths for Knoke information exchange
We see that most of the geodesic connections among these actors are not only short distance, but that there are very often multiple shortest paths from x to y. This suggests a couple things: information flow is not likely to break down, because there are multiple paths; and, it will be difficult for any individual to be a powerful "broker" in this structure because most actors have alternative efficient ways of connection to other actors that can bypass any given actor.
Flow
The use of geodesic paths to examine properties of the distances between individuals and for the whole network often makes a great deal of sense. But, there may be other cases where the distance between two actors, and the connectedness of the graph as a whole is best though of as involving all connections - not just the most efficient ones. If I start a rumor, for example, it will pass through a network by all pathways - not just the most efficient ones. How much credence another person gives my rumor may depend on how many times they hear it from different sources - and not how soon they hear it. For uses of distance like this, we need to take into account all of the connections among actors.
Several approaches have been developed for counting the amount of connection between pairs of actors that take into account all connections between them. These measures have been used for a number of different purposes, and these differences are reflected in the algorithms used to calculate them.
Network>Cohesion>Maximum Flow. One notion of how totally connected two actors are (called maximum flow by UCINET) asks how many different actors in the neighborhood of a source lead to pathways to a target. If I need to get a message to you, and there is only one other person to whom I can send this for retransmission, my connection is weak -even if the person I send it to may have many ways of reaching you. If, on the other hand, there are four people to whom I can send my message, each of whom has one or more ways of retransmitting my message to you, then my connection is stronger. The "flow" approach suggests that the strength of my tie to you is no stronger than the weakest link in the chain of connections, where weakness means a lack of alternatives. This approach to connection between actors is closely connected to the notion of betweenness that we will examine a bit later. It is also logically close to the idea that the number of pathways, not their length, may be important in connecting people. For our directed information flow data, the results of UCINET's count of maximum flow are shown in Figure 7.17.
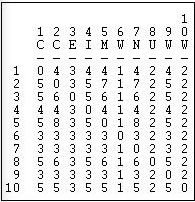
Figure 7.17: Maximum flow for Knoke information network
You should verify for yourself that, for example, there are four intermediaries, or alternative routes, in flows from actor 1 to actor 2, but five such points in the flow from actor 2 to actor 1. The higher the number of flows from one actor to another, the greater the likelihood that communication will occur, and the less "vulnerable" the connection. Note that actors 6, 7, and 9 are relatively disadvantaged. In particular, actor 6 has only one way of obtaining information from all other actors (the column vector of flows to actor 6).


