13.3: Visualizing Similarity and Distance
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the previous section, we've seen how the degree of similarity or distance between two actors patterns of ties with other actors can be measured and indexed. Once this is done, then what?
It is often useful to examine the similarities or distances to try to locate groupings of actors (that is, larger than a pair) who are similar. By studying the bigger patterns of which groups of actors are similar to which others, we may also gain some insight into "what about" the actor's positions is most critical in making them more similar or more distant.
Two tools that are commonly used for visualizing patterns of relationships among variables are also very helpful in exploring social network data. When we have created a similarity or distance matrix describing all the pairs of actors, we can study the similarity of differences among "cases" relations in the same way that we would study similarities among attributes.
In the next two sections we will show very brief examples of how multi-dimensional scaling and hierarchical cluster analysis can be used to identify patterns in actor-by-actor similarity/distance matrices. Both of these tools are widely used in non-network analysis; there are large and excellent literatures on the many important complexities of using these methods. Our goal here is just to provide just a very basic introduction.
Clustering Tools
Agglomerative hierarchical clustering of nodes on the basis of the similarity of their profiles of ties to other cases provides a "joining tree" or "dendogram" that visualizes the degree of similarity among cases - and can be used to find approximate equivalence classes.
Tools>Cluster>Hierarchical proceeds by initially placing each case in its own cluster. The two most similar cases (those with the highest measured similarity index) are then combined into a class. The similarity of this new class to all others is then computed on the basis of one of three methods. On the basis of the newly computed similarity matrix, the joining/recalculation process is repeated until all cases are "agglomerated" into a single cluster. The "hierarchical" part of the method's name refers to the fact that once a case has been joined into a cluster, it is never re-classified. This results in clusters of increasing size that always enclose smaller clusters.
The "Average" method computes the similarity of the average scores in the newly formed cluster to all other clusters; the "Single-Link" method (a.k.a. "nearest neighbor") computes the similarities on the basis of the similarity of the member of the new cluster that is most similar to each other case not in the cluster. The "Complete-Link" method (a.k.a. "farthest neighbor") computes similarities between the member of the new cluster that is least similar to each other case not in the cluster. The default method is to use the cluster average; single-link methods will tend to give long, stringy joining diagrams; complete-link methods will tend to give highly separated joining diagrams.
The Hamming distance in information sending in the Knoke network was computed as shown in the section above, and the results were store as a file. This file was then input to Tools>Cluster>Hierarchical. We specified that the "average" method was to be used, and that the data were "dissimilarities". The results are shown as Figure 13.9.
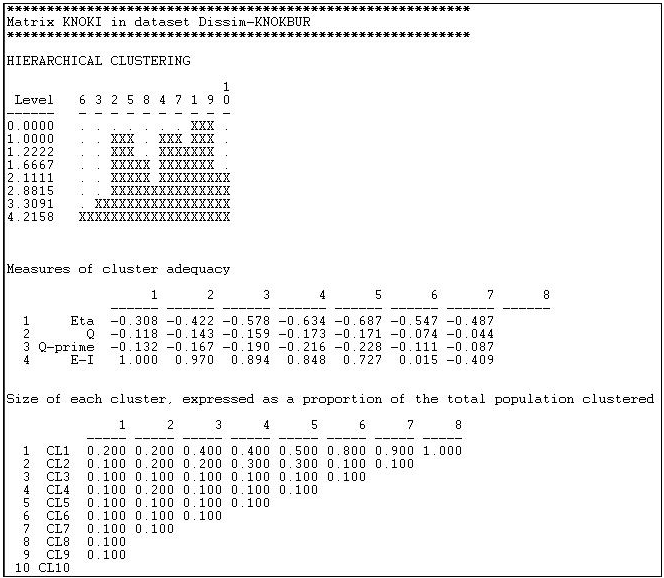
Figure 13.9: Clustering of Hamming distances of information sending in the Knoke network
The first graphic shows that nodes 1 and 9 were the most similar, and joined first. The graphic, by the way, can be rendered as a more polished dendogram using Tools>Dendogram>Draw on data saved from the cluster tool. At the next step, there are three clusters (cases 2 and 5, 4 and 7, and 1 and 9). The joining continues until (at the 8th step) all cases are agglomerated into a single cluster. This gives a clear picture of the similarity of cases, and the groupings or classes of cases. But there are really eight pictures here (one for each step of the joining). Which is the "right" solution?
Again, there is no single answer. Theory and a substantive knowledge of the processes giving rise to the data are the best guide. The second panel "Measures of cluster adequacy" can be of some assistance. There are a number of indexes here, and most will (usually) give similar answers. As we move from the right (higher steps or amounts of agglomeration) to the left (more clusters, less agglomeration) fit improves. The E-I index is often most helpful, as it measures the ratio of the numbers of ties within the clusters to ties between clusters. Generally, the goal is to achieve classes that are highly similar within, and quite distinct without. Here, one might be most tempted by the solution of the 5th step of the process (clusters of 2+5, 4+7, 1+9, and the others being single-item clusters).
To be meaningful, clusters should also contain a reasonable percentage of the cases. The last panel shows information on the relative sizes of the clusters at each stage. With only 10 cases to be clustered in our example, this is not terribly enlightening here.
UCINET provides two additional cluster analysis tools that we won't discuss at any length here - but which you may wish to explore. Tools>Cluster>Optimization allows the user to select, a priori, a number of classes, and then uses the chosen cluster analysis method to optimally fit cases to classes. This is very similar to the structural optimization technique we will discuss below. Tools>Cluster>Cluster Adequacy takes a user-supplied classification (a partition, or attribute file), fits the data to it, and reports on the goodness of fit.
Multi-Dimensional Scaling Tools
Usually our goal in equivalence analysis is to identify and visualize "classes" or clusters of cases. In using cluster analysis, we are implicitly assuming that the similarity or distance among cases reflects as single underlying dimension. It is possible, however, that there are multiple "aspects" or "dimensions" underlying the observed similarities of cases. Factor or component analysis could be applied to correlations or covariances among cases. Alternatively, multi-dimensional scaling could be used (non-metric for data that are inherently nominal or ordinal; metric for valued).
MDS represents the patterns of similarity or dissimilarity in the tie profiles among the actors (when applied to adjacency or distances) as a "map" in multi-dimensional space. This map lets us see how "close" actors are, whether they "cluster" in multi-dimensional space, and how much variation there is along each dimension.
Figures 13.10 and 13.11 show the results of applying Tools>MDS>Non-Metric MDS to the raw adjacency matrix of the Knoke information network, and selecting a two-dimensional solution.
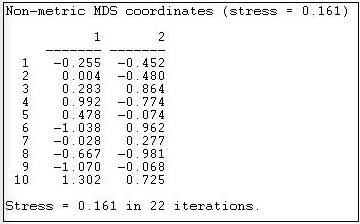
Figure 13.10: Non-metric MDS two-dimensional coordinates of Knoke information adjacency
"Stress" is a measure of badness of fit. In using MDS, it is a good idea to look at a range of solutions with more dimensions, so you can assess the extent to which the distances are uni-dimensional. The coordinates show the location of each case (1 through 10) on each of the dimensions. Case one, for example, is in the lower left quadrant, having negative scores on both dimension 1 and dimension 2.
The "meaning" of the dimensions can sometimes be assessed by comparing cases that are at the extreme poles of each dimension. Are the organizations at one pole "public" and those at the other "private"? In analyzing social network data, it is not unusual for the first dimension to be simply the amount of connection or the degree of the nodes.
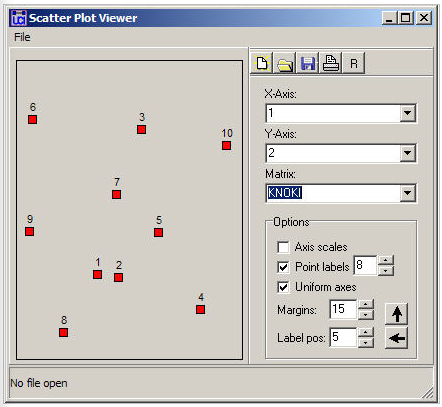
Figure 13.11: Two-dimensional map of non-metric MDS of Knoke information adjacency
Figure 13.11 graphs the nodes according to their coordinates. In this map, we are looking for meaningful tight clusters of points to identify cases that are highly similar on both dimensions. In our example, there is very little such similarity (save, perhaps, nodes 1 and 2).
Clustering and scaling tools can be useful in many kinds of network analysis. Any measure of the relations among nodes can be visualized using these methods - adjacency, strength, correlation, and distance are most commonly examined.
These tools are also quite useful for examining equivalence. Most methods for assessing equivalence generate actor-by-actor measures of closeness or similarity in the tie profiles (using different rules, depending on what type of equivalence we are trying to measure). Cluster and MDS are often quite helpful in making sense of the results.


