13.2: Measuring Similarity/Dissimilarity
- Page ID
- 7729
We might try to assess which nodes are most similar to which other nodes intuitively by looking at a graph. We would notice some important things. It would seem that actors 2, 5 and 7 might be structurally similar in that they seem to have reciprocal ties with each other and almost everyone else. Actors 6, 8, and 10 are "regularly" similar in that they are rather isolated, but they are not structurally similar because they are connected to quite different sets of actors. But, beyond this, it is really rather difficult to assess equivalence rigorously by just looking at a diagram.
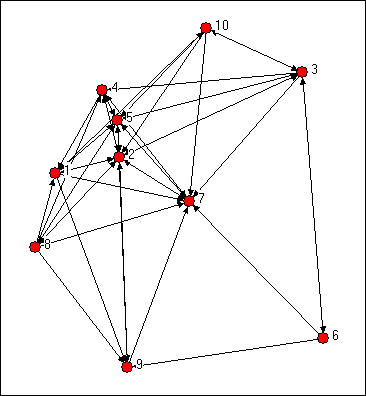
Figure 13.1: Knoke directed information network
We can be a lot more precise in assessing similarity if we use the matrix representation of the network instead of the diagram. This also lets us use the computer to do some of the quite tedious jobs involved in calculating index numbers to assess similarity. The original data matrix has been reproduced below as Figure 13.2. Many of the features that were apparent in the diagram are also easy to grasp in the matrix. If we look across the rows and count out-degrees, and if we look down the columns (to count in-degree) we can see who the central actors are and who are the isolates. But, even more generally, we can see that two actors are structurally equivalent to the extent that the profile of scores in their rows and columns are similar. Finding automorphic equivalence and regular equivalence is not so simple. But, since these other forms are less restrictive (and hence simplifications of the structural classes), we begin by measuring how similar each actor's ties are to all other actors.
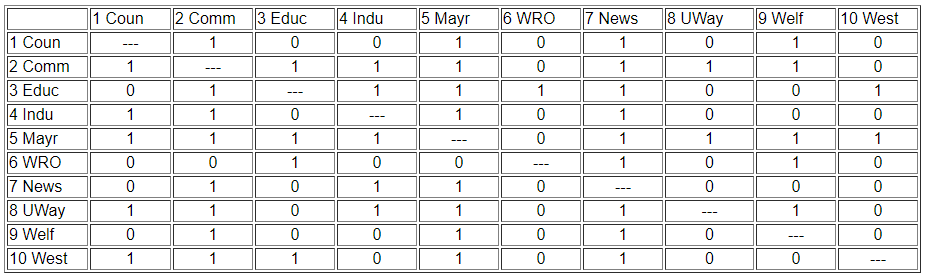
Figure 13.2: Adjacency matrix for Knoke information network
Two actors may be said to be structurally equivalent if they have the same patterns of ties with other actors. This means that the entries in the rows and columns for one actor are identical to those of another. If the matrix were symmetric, we would need only to scan pairs of rows (or columns). But, since these data are on directed ties, we should examine the similarity of sending and receiving of ties (of course, we might be interested in structural equivalence with regard to only sending, or only receiving ties). We can see the similarity of the actors if we expand the matrix in Figure 13.2 by listing the row vectors followed by the column vectors for each actor as a single column, as we have in Figure 13.3.
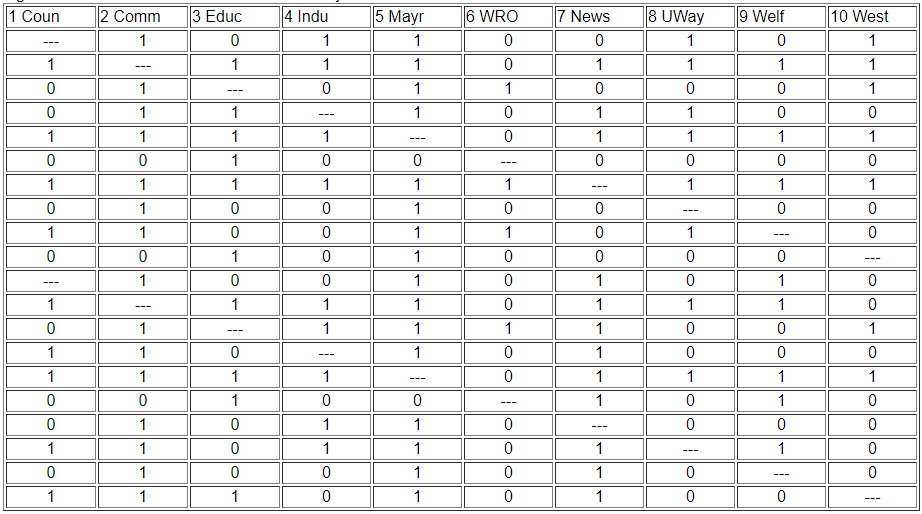
Figure 13.3: Concatenated row and column adjacencies for Knoke information network
The ties of each actor (both in and out) are now represented as a column of data. We can now measure the similarity of each pair of columns to index the similarity of the two actors, forming a pair-wise matrix of similarities. We could also get at the same idea in reverse, by indexing the dissimilarity or "distance" between the scores in any two columns.
There are any number of ways to index similarity and distance. In the next two sections we'll briefly review the most commonly used approaches when the ties are measured as values (i.e. strength or cost or probability) and as binary.
The goal here is to create an actor-by-actor matrix of the similarity (or distance) measures. Once we have done this, we can apply other techniques for visualizing the similarities in the actor's patterns of relations with other actors.
Valued Relations
A common approach for indexing the similarity of two valued variables is the degree of linear association between the two. Exactly the same approach can be applied to the vectors that describe the relationship strengths of two actors to all other actors. As with any measures of linear association, linearity is a key assumption. It is often wise, even when data are at the interval level (e.g. volume of trade from one nation to all others) to consider measures with weaker assumptions (like measures of association designed for ordinal variables).
Pearson Correlation Coefficients, Covariances, and Cross-Products
The correlation measure of similarity is particularly useful when the data on ties are "valued", that is, tell us about the strength and direction of association, rather than simple presence or absence. Pearson correlations range from -1.00 (meaning that the two actors have exactly the opposite ties to each other), through zero (meaning that knowing one actor's tie to a third party doesn't help us at all in guessing what the other actor's tie to the third party might be), to +1.00 (meaning that the two actors always have exactly the same tie to other actors - perfect equivalence). Pearson correlations are often used to summarize pair-wise structural equivalence because the statistic (called "little r") is widely used in social statistics. If the data on ties are truly nominal, or if density is very high or very low, correlations can sometimes be a little troublesome, and matches (see below) should also be examined. Different statistics, however, usually give very much the same answers. Figure 13.4 shows the correlations of the ten Knoke organization's profiles of in and out information ties. We are applying correlation, even though the Knoke data are binary. The UCINET algorithm Tools>Similarities will calculate correlations for rows or columns.
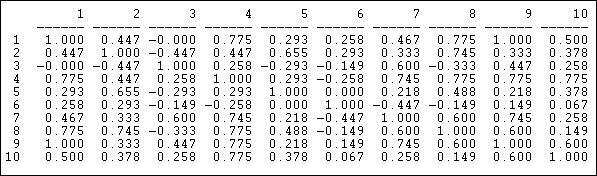
Figure 13.4: Pearson correlations of rows (sending) for Knoke information network
We can see, for example, that node 1 and node 9 have identical patterns of ties; there is a moderately strong tendency for actor 6 to have ties to actors that actor 7 does not, and vice versa.
The Pearson correlation measure does not pay attention to the overall prevalence of ties (the mean of the row or column), and it does not pay attention to differences between actors in the variances of their ties. Often this is desirable - to focus only on the pattern, rather than the mean and variance as aspects of similarity between actors.
Often though, we might want our measure of similarity to reflect not only the pattern of ties, but also differences among actors in their overall tie density. Tools>Similarities will also calculate the covariance matrix. If we want to include differences in variances across actors as aspects of (dis)similarity, as well as means, the cross-product ratio calculated in Tools>Similarities might be used.
Euclidean, Manhattan, and Squared Distances
An alternative approach to linear correlation (and its relatives) is to measure the "distance" or "dissimilarity" between the tie profiles of each pair of actors. Several "distance" measures are fairly commonly used in network analysis, particularly the Euclidean distance or squared Euclidean distance. These measures are not sensitive to the linearity of association and can be used with either valued or binary data.
Figure 13.5 shows the Euclidean distances among the Knoke organizations calculated using Tools>Dissimilarities and Distances>Std Vector dissimilarities/distances.

Figure 13.5: Euclidean distances in sending for Knoke information network
The Euclidean distance between two vectors is equal to the square root of the sum of the squared differences between them. That is, the strength of actor A's tie to C is subtracted from the strength of actor B's tie to C, and the difference is squared. This is then repeated across all the other actors (D, E, F, etc.), and summed. The square root of the sum is then taken.
A closely related measure is the "Manhattan" or block distance between the two vectors. This distance is simply the sum of the absolute difference between the actor's ties to each alter, summed across the alters.
Binary Relations
If the information that we have about the ties among our actors is binary, correlation and distance measures can be used, but may not be optimal. For data that are binary, it is more common to look at the vectors of two actor's ties, and see how closely the entries in one "match" the entries in the other.
There are several useful measures of tie profile similarity based on the matching idea that are calculated by Tools>Similarities.
Matches: Exact, Jaccard, Hamming
A very simple and often effective approach to measuring the similarity of two tie profiles is to count the number of times that actor A's tie to alter is the same as actor B's tie to alter, and express this as a percentage of the possible total.
Figure 13.6 shows the result for the columns (information receiving) relation of the Knoke bureaucracies.
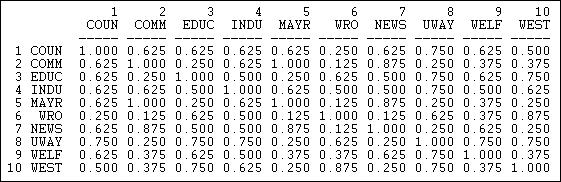
Figure 13.6: Proportion of matches for Knoke information receiving
These results show similarity in a way that is quite easy to interpret. The number 0.625 in the cell 2,1 means that, in comparing actor #1 and #2, they have the same tie (present or absent) to other actors \(62.5\%\) of the time. The measure is particularly useful with multi-category nominal measures of ties; it also provides a nice scaling for binary data.
In some networks connections are very sparse. Indeed, if one were looking at ties of personal acquaintance in very large organizations, the data might have very low density. Where density is very low, the "matches", "correlation", and "distance" measures can all show relatively little variation among the actors, and may cause difficulty in discerning structural equivalence sets (of course, in very large, low density networks, there may really be very low levels of structural equivalence).
One approach to solving this problem is to calculate the number of times that both actors report a tie (or the same type of tie) to the same third actors as a percentage of the total number of ties reported. That is, we ignore cases where neither X nor Y are tied to Z, and ask, of the total ties that are present, what percentage are in common. Figure 13.7 shows the Jaccard coefficients for information receiving in the Knoke network, calculated using Tools>Similarities, and selecting "Jaccard".
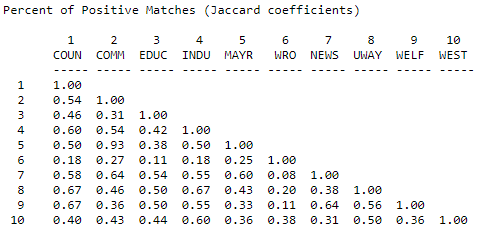
Figure 13.7: Jaccard coefficients for information receiving profiles in Knoke network
Again the same basic picture emerges. The uniqueness of actor #6, though, is emphasized. Actor 6 is more unique by this measure because of the relatively small number of total ties that it has - this results in a lower level of similarity when "joint absence" of ties are ignored. Where data are sparse, and where there are very substantial differences in the degrees of points, the positive match coefficient is a good choice for binary or nominal data.
Another interesting "matching" measure is the Hamming distance, shown in Figure 13.8.
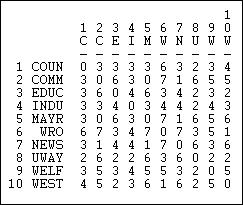
Figure 13.8: Hamming distances of information receiving in Knoke network
The Hamming distance is the number of entries in the vector for one actor that would need to be changed in order to make it identical to the vector of the other actor. These differences could be either adding or dropping a tie, so the Hamming distance treats joint absence as similarity.
With some inventiveness, you can probably think of some other reasonable ways of indexing the degree of structural similarity between actors. You might look at the program "Proximities" by SPSSx, which offers a large collection of measures of similarity. The choice of a measure should be driven by a conceptual notion of "what about" the similarity of two tie profiles is most important for the purposes of a particular analysis. Often, frankly, it makes little difference, but that is hardly sufficient grounds to ignore the question.


