13.2: Fundamentals of Vector Calculus
( \newcommand{\kernel}{\mathrm{null}\,}\)
In order to develop continuous field models, you need to know some basic mathematical concepts developed and used in vector calculus. A minimalistic quick review of those concepts is given in the following.
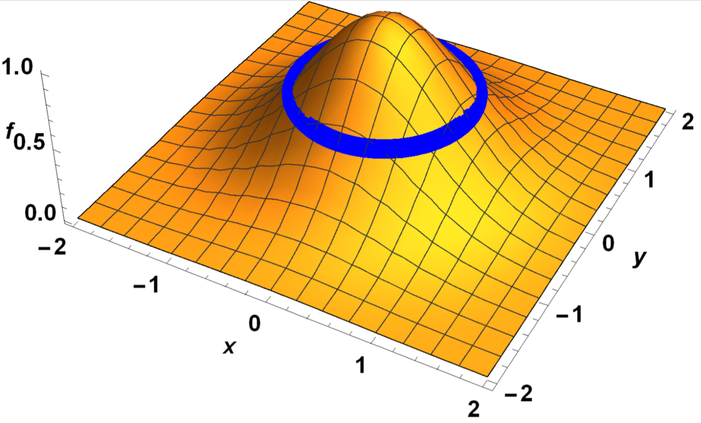
A contour is a set of spatial positions x that satisfy
f(x)=C
for a scalar field f, where C is a constant (see an example in Figure 13.2.1). Contours are also called level curves or surfaces.
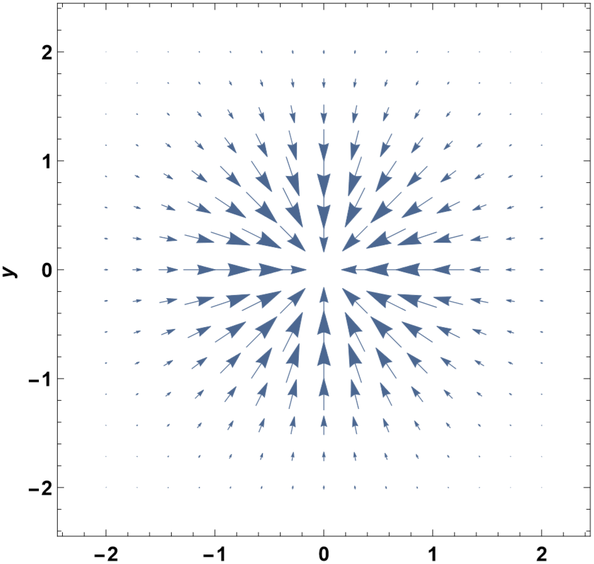
A gradient of a scalar field f is a vector locally defined as
∇f=(∂f∂x1∂f∂x2⋮∂f∂xn)
Here, n is the number of dimensions of the space.
The symbol ∇ is called “del” or “nabla,” which can be considered the following “vector” of differential operators:
∇=(∂∂x1∂∂x2⋮∂∂xn)
A gradient of f at position x is a vector pointing toward the direction of the steepest ascending slope of f at x. The length of the vector represents how steep the slope is. A vector field of gradient ∇f defined over a scalar field f is often called a gradient field (See an example in Figure 13.2.2). The gradient is always perpendicular to the contour that goes through x (unless the gradient is a zero vector; compare Figs. 13.2.1 and 13.2.2).
A divergence of a vector field v is a scalar field defined as
∇⋅v=(∂∂x1∂1∂x2⋮∂xn)T(v1v2⋮vn)=∂v1∂x1+∂v2∂x2+…+∂vn∂xn.
Note the tiny dot between ∇ and v, which indicates that this is an “inner product” of them. Don’t confuse this divergence with the gradient discussed above!
The physical meaning of divergence is not so straightforward to understand, but anyway, it literally quantifies how much the vector field v is “diverging” from the location x. Let’s go through an example for a 2-D space. Assume that v is representing flows of some “stuff” moving around in a 2-D space. The stuff is made of a large number of particles (like a gas made of molecules), and the flow v=(vx,vy) means how many particles are going through a cross-section of the space per area per unit of time. In this 2-D example, a cross-section means a line segment in the space, and the total area of the section is just the length of the line segment.
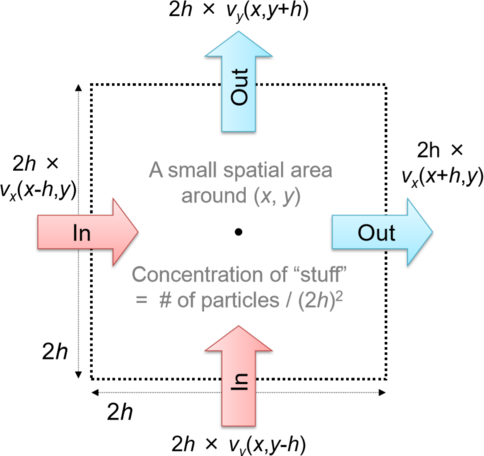
Then, consider a temporal change of the number of particles, say N, within a very small spatial area around (x,y) Figure 13.2.3. The temporal change of N can be calculated by counting how many particles are coming into/going out of the area through each edge per unit of time, as
∂N∂t=2hvx(x−h,y)+2hvy(x,y−h)−2hvx(x+h,y)−2hvy(x,y+h),
where h is the distance from (x,y) to each edge, and therefore the length of each edge is 2h.
Actually, Figure 13.2.3 may be a bit misleading; the particles can go in and out through any edge in both directions. But we use the + sign for vx(x−h,y) and vy(x,y−h) and the − sign for vx(x+h,y) and vy(x,y+h) in Eq. (???), because the velocities are measured using the coordinate system where the rightward and upward directions are considered positive.
Since N depends on the size of the area, we can divide it by the area ((2h)2 in this case) to calculate the change in terms of the concentration of the particles, c=N/(2h)2, which won’t depend on h:
∂c∂t=2hvx(x−h,y)+2hvy(x,y−h)−2hvx(x+h,y)−2hvy(x,y+h)(2h)2=vx(x−h,y)+vy(x,y−h)−vx(x+h,y)−vy(x,y+h)2h
If we make the size of the area really small (h→0), this becomes the following:
∂c∂t=limh→0vx(x−h,y)+vy(x,y−h)−vx(x+h,y)−vx(x+h,y)−vy(x,y+h)2h=limh→0{(−vx(x+h,y)−vx(x−h,y)2h)+(−vy(x,y+h)−vy(x,y−h)2h)}=−∂vx∂x−∂vy∂y=−∇⋅v
In natural words, this means that the temporal change of a concentration of the stuff is given by a negative divergence of the vector field v that describes its movement. If the divergence is positive, that means that the stuff is escaping from the local area. If the divergence is negative, the stuff is flowing into the local area. The mathematical derivation above confirms this intuitive understanding of divergence
Confirm that the interpretation of divergence above also applies to 3-D cases.
A Laplacian of a scalar field f is a scalar field defined as
∇2f=∇⋅∇f=(∂∂x1∂∂x2⋮∂∂xn)T(∂∂x1∂∂x2⋮∂∂xn)f=∂2f∂x21+∂2f∂x22+...+∂2f∂x2n.
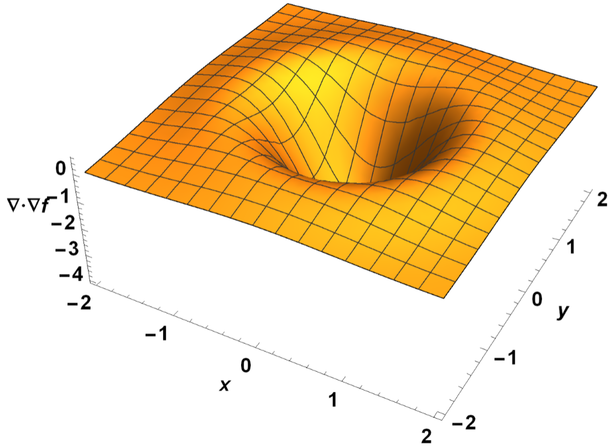
Sometimes the Laplacian operator is denoted by a right side up triangle ∆ instead of ∇^2. This is so confusing, I know, but blame the people who invented this notation. In this textbook, we use ∇^2 instead of ∆ to denote Laplacians, because ∇^2 is more intuitive to show it is a second-order differential operator, and also because ∆ is already used to represent small quantities (e.g., ∆x).
The gradient field of f shows a diverging pattern where the scalar field f is concave like a dip or a valley, or a converging pattern where f is convex like a hump or a ridge. Therefore, the Laplacian of f, which is the divergence of the gradient field off, has a positive value where f is concave, or a negative value where f is convex. This is similar to the second-order derivative of a mathematical function; a concave function has a positive second-order derivative while a convex function has a negative one. The Laplacian is a generalization of the same concept, applicable to functions defined over a multidimensional domain.
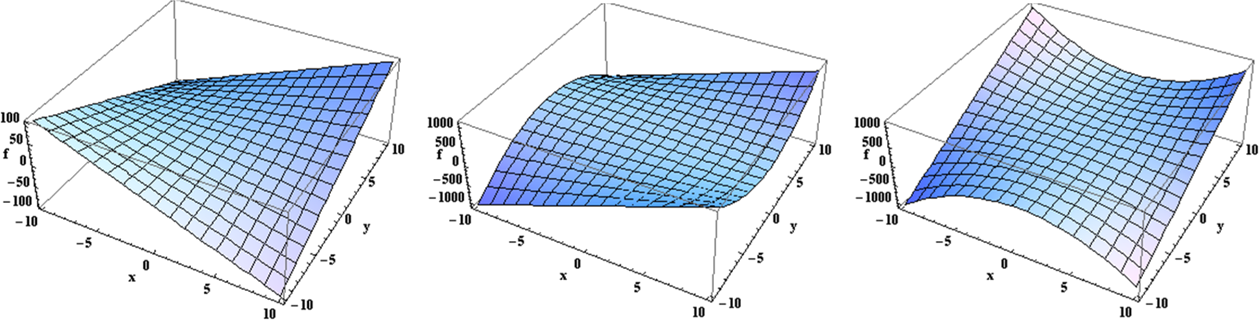
Which of the following surface plots correctly illustrates the shape of a scalar field f(x,y) = xy(x−1)?
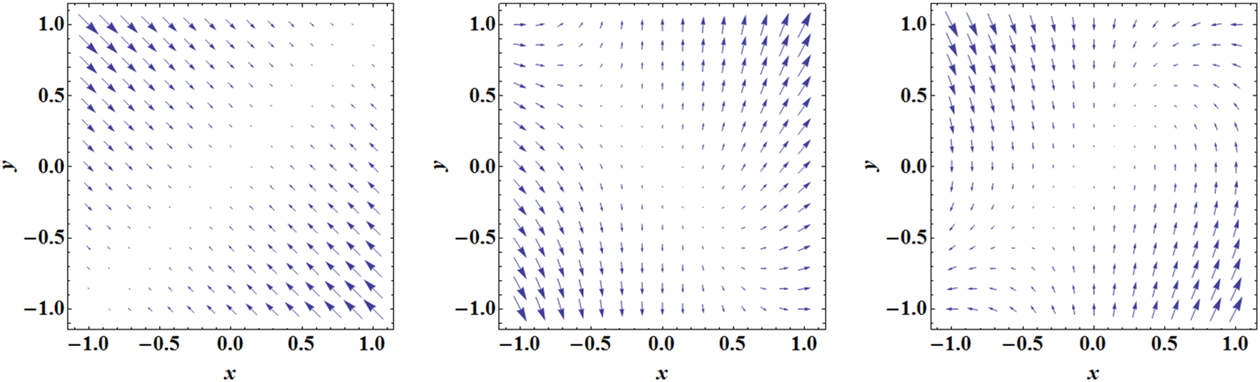
Which of the following vector field plots correctly illustrates the flows given by a vector field v(x,y) = (−xy,x−y)?
Calculate the gradient field and the Laplacian of each of the following:
- f(x, y) =x^{2} +xy
- f(x,y) =e^{x+y}
- f(x, y, z) =\frac{x+y}{z}
Explain where in the x-y space the surface defined by f(x,y) = 3x^{2} −xy^{3} switches between concave and convex.
So far, the gradient is defined only for a scalar field, but it is natural to define a gradient for a vector field too. Propose a meaningful definition of ∇v and discuss its physical meaning.


