1.3: Problem Solving Strategies
- Page ID
- 9823
Think back to the first problem in this chapter, the ABC Problem. What did you do to solve it? Even if you did not figure it out completely by yourself, you probably worked towards a solution and figured out some things that did not work.
Unlike exercises, there is never a simple recipe for solving a problem. You can get better and better at solving problems, both by building up your background knowledge and by simply practicing. As you solve more problems (and learn how other people solved them), you learn strategies and techniques that can be useful. But no single strategy works every time.
George Pólya was a great champion in the field of teachingeffective problem solving skills. He was born in Hungary in 1887, received his Ph.D. at the University of Budapest, and was a professor at Stanford University (among other universities). He wrote many mathematical papers along with three books, most famously, “How to Solve it.” Pólya died at the age 98 in 1985.[1]

George Pólya, circa 1973
- Image of Pólya by Thane Plambeck from Palo Alto, California (Flickr) [CC BY 2.0 (http://creativecommons.org/licenses/by/2.0)], via Wikimedia Commons ↵
In 1945, Pólya published the short book How to Solve It, which gave a four-step method for solving mathematical problems:
- First, you have to understand the problem.
- After understanding, then make a plan.
- Carry out the plan.
- Look back on your work. How could it be better?
This is all well and good, but how do you actually do these steps?!?! Steps 1. and 2. are particularly mysterious! How do you “make a plan?” That is where you need some tools in your toolbox, and some experience to draw upon.
Much has been written since 1945 to explain these steps in more detail, but the truth is that they are more art than science. This is where math becomes a creative endeavor (and where it becomes so much fun). We will articulate some useful problem solving strategies, but no such list will ever be complete. This is really just a start to help you on your way. The best way to become a skilled problem solver is to learn the background material well, and then to solve a lot of problems!
We have already seen one problem solving strategy, which we call “Wishful Thinking.” Do not be afraid to change the problem! Ask yourself “what if” questions:
- What if the picture was different?
- What if the numbers were simpler?
- What if I just made up some numbers?
You need to be sure to go back to the original problem at the end, but wishful thinking can be a powerful strategy for getting started.
This brings us to the most important problem solving strategy of all:
Problem Solving Strategy 2 (Try Something!).
If you are really trying to solve a problem, the whole point is that you do not know what to do right out of the starting gate. You need to just try something! Put pencil to paper (or stylus to screen or chalk to board or whatever!) and try something. This is often an important step in understanding the problem; just mess around with it a bit to understand the situation and figure out what is going on.
And equally important: If what you tried first does not work, try something else! Play around with the problem until you have a feel for what is going on.
Last week, Alex borrowed money from several of his friends. He finally got paid at work, so he brought cash to school to pay back his debts. First he saw Brianna, and he gave her 1/4 of the money he had brought to school. Then Alex saw Chris and gave him 1/3 of what he had left after paying Brianna. Finally, Alex saw David and gave him 1/2 of what he had remaining. Who got the most money from Alex?
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem? This problem lends itself to two particular strategies. Did you try either of these as you worked on the problem? If not, read about the strategy and then try it out before watching the solution.
Problem Solving Strategy 3 (Draw a Picture).
Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help! Can you represent something in the situation by a picture?
Draw a square to represent all of Alex’s money. Then shade 1/4 of the square — that’s what he gave away to Brianna. How can the picture help you finish the problem?
After you have worked on the problem yourself using this strategy (or if you are completely stuck), you can watch someone else’s solution.
Problem Solving Strategy 4 (Make Up Numbers).
Part of what makes this problem difficult is that it is about money, but there are no numbers given. That means the numbers must not be important. So just make them up!
You can work forwards: Assume Alex had some specific amount of money when he showed up at school, say $100. Then figure out how much he gives to each person. Or you can work backwards: suppose he has some specific amount left at the end, like $10. Since he gave Chris half of what he had left, that means he had $20 before running into Chris. Now, work backwards and figure out how much each person got.
Watch the solution only after you tried this strategy for yourself.
If you use the “Make Up Numbers” strategy, it is really important to remember what the original problem was asking! You do not want to answer something like “Everyone got $10.” That is not true in the original problem; that is an artifact of the numbers you made up. So after you work everything out, be sure to re-read the problem and answer what was asked!
How many squares, of any possible size, are on a 8 × 8 chess board? (The answer is not 64... It’s a lot bigger!)
Remember Pólya’s first step is to understand the problem. If you are not sure what is being asked, or why the answer is not just 64, be sure to ask someone!
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What did you figure out about the problem, even if you have not solved it completely?
It is clear that you want to draw a picture for this problem, but even with the picture it can be hard to know if you have found the correct answer. The numbers get big, and it can be hard to keep track of your work. Your goal at the end is to be absolutely positive that you found the right answer. You should never ask the teacher, “Is this right?” Instead, you should declare, “Here’s my answer, and here is why I know it is correct!”
Problem Solving Strategy 5 (Try a Simpler Problem).
Pólya suggested this strategy: “If you can’t solve a problem, then there is an easier problem you can solve: find it.” He also said: “If you cannot solve the proposed problem, try to solve first some related problem. Could you imagine a more accessible related problem?” In this case, an 8 × 8 chess board is pretty big. Can you solve the problem for smaller boards? Like 1 × 1? 2 × 2? 3 × 3?
Of course the ultimate goal is to solve the original problem. But working with smaller boards might give you some insight and help you devise your plan (that is Pólya’s step (2)).
Problem Solving Strategy 6 (Work Systematically).
If you are working on simpler problems, it is useful to keep track of what you have figured out and what changes as the problem gets more complicated.
For example, in this problem you might keep track of how many 1 × 1 squares are on each board, how many 2 × 2 squares on are each board, how many 3 × 3 squares are on each board, and so on. You could keep track of the information in a table:
| size of board | # of 1 × 1 squares | # of 2 × 2 squares | # of 3 × 3 squares | # of 4 × 4 squares | … |
| 1 by 1 | 1 | 0 | 0 | 0 | |
| 2 by 2 | 4 | 1 | 0 | 0 | |
| 3 by 3 | 9 | 4 | 1 | 0 | |
| … |
Problem Solving Strategy 7 (Use Manipulatives to Help You Investigate).
Sometimes even drawing a picture may not be enough to help you investigate a problem. Having actual materials that you move around can sometimes help a lot!
For example, in this problem it can be difficult to keep track of which squares you have already counted. You might want to cut out 1 × 1 squares, 2 × 2 squares, 3 × 3 squares, and so on. You can actually move the smaller squares across the chess board in a systematic way, making sure that you count everything once and do not count anything twice.
Problem Solving Strategy 8 (Look for and Explain Patterns).
Sometimes the numbers in a problem are so big, there is no way you will actually count everything up by hand. For example, if the problem in this section were about a 100 × 100 chess board, you would not want to go through counting all the squares by hand! It would be much more appealing to find a pattern in the smaller boards and then extend that pattern to solve the problem for a 100 × 100 chess board just with a calculation.
If you have not done so already, extend the table above all the way to an 8 × 8 chess board, filling in all the rows and columns. Use your table to find the total number of squares in an 8 × 8 chess board. Then:
- Describe all of the patterns you see in the table.
- Can you explain and justify any of the patterns you see? How can you be sure they will continue?
- What calculation would you do to find the total number of squares on a 100 × 100 chess board?
(We will come back to this question soon. So if you are not sure right now how to explain and justify the patterns you found, that is OK.)
This clock has been broken into three pieces. If you add the numbers in each piece, the sums are consecutive numbers. (Consecutive numbers are whole numbers that appear one after the other, such as 1, 2, 3, 4 or 13, 14, 15.)
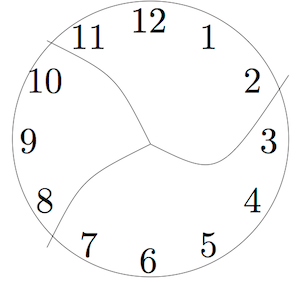
Can you break another clock into a different number of pieces so that the sums are consecutive numbers? Assume that each piece has at least two numbers and that no number is damaged (e.g. 12 isn’t split into two digits 1 and 2.)
Remember that your first step is to understand the problem. Work out what is going on here. What are the sums of the numbers on each piece? Are they consecutive?
After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it). What did you try? What progress have you made?
Problem Solving Strategy 9 (Find the Math, Remove the Context).
Sometimes the problem has a lot of details in it that are unimportant, or at least unimportant for getting started. The goal is to find the underlying math problem, then come back to the original question and see if you can solve it using the math.
In this case, worrying about the clock and exactly how the pieces break is less important than worrying about finding consecutive numbers that sum to the correct total. Ask yourself:
- What is the sum of all the numbers on the clock’s face?
- Can I find two consecutive numbers that give the correct sum? Or four consecutive numbers? Or some other amount?
- How do I know when I am done? When should I stop looking?
Of course, solving the question about consecutive numbers is not the same as solving the original problem. You have to go back and see if the clock can actually break apart so that each piece gives you one of those consecutive numbers. Maybe you can solve the math problem, but it does not translate into solving the clock problem.
Problem Solving Strategy 10 (Check Your Assumptions).
When solving problems, it is easy to limit your thinking by adding extra assumptions that are not in the problem. Be sure you ask yourself: Am I constraining my thinking too much?
In the clock problem, because the first solution has the clock broken radially (all three pieces meet at the center, so it looks like slicing a pie), many people assume that is how the clock must break. But the problem does not require the clock to break radially. It might break into pieces like this:
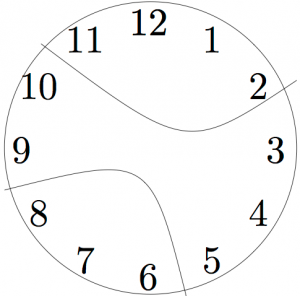
Were you assuming the clock would break in a specific way? Try to solve the problem now, if you have not already.


