2.2: Other Rules
- Page ID
- 9829
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Let’s play the dots and boxes game, but change the rule.
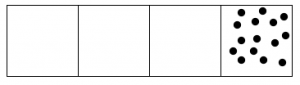
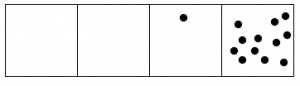
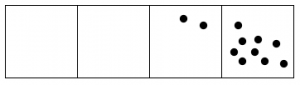
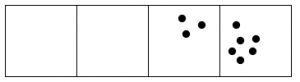
Whenever there are three dots in single box, they “explode,” disappear, and become one dot in the box to the left.
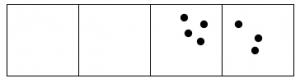
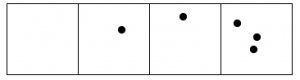
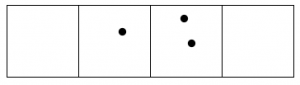
Here’s what happens with fifteen dots:
- Answer
-
The 1←3 code for fifteen dots is: 120.
- Show that the 1←3 code for twenty dots is 202.
- What is the 1←3 code for thirteen dots?
- What is the 1←3 code for twenty-five dots?
- What number of dots has 1←3 code 1022?
- Is it possible for a collection of dots to have 1←3 code 2031? Explain your answer.
- Describe how the 1←4 rule would work.
- What is the 1←4 code for thirteen dots?
- What is the 1←5 code for the thirteen dots?
- What is the 1←5 code for five dots?
- What is the 1←9 code for thirteen dots?
- What is the 1←9 code for thirty dots?
- What is the 1←10 code for thirteen dots?
- What is the 1←10 code for thirty-seven dots?
- What is the 1←10 code for two hundred thirty-eight dots?
- What is the 1←10 code for five thousand eight hundred and thirty-three dots?
After you have worked on the problems on your own, compare your ideas with a partner. Can you describe what’s going on in Problem 6 and why?


