3.5: Division- Dots and Boxes
- Page ID
- 9839
Quotative Model of Division
Suppose you are asked to compute 3906 : 3. One way to interpret this question (there are others) is:
“How many groups of 3 fit into 3906?”
In the quotative model of division, you are given a dividend (here it is 3906), and you are asked to split it into equal-sized groups, where the size of the group is given by the divisor (here it is 3).
In our dots and boxes model, the dividend 3906 looks like this:
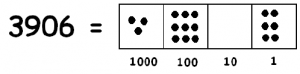
and three dots looks like this: 
So we are really asking:
“How many groups of  fit into the picture of 3906?”
fit into the picture of 3906?”
There is one group of 3 at the thousands level, and three at the hundreds level, none at the tens level, and two at the ones level.
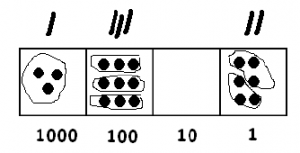
Notice what we have in the picture:
- One group of 3 in the thousands box.
- Three groups of 3 in the hundreds box.
- Zero groups of 3 in the tens box.
- Two groups of 3 in the ones box.
This shows that 3 goes into 3906 one thousand, three hundreds and two ones times. That is,
\[3906 \div 3 = 1302 \ldotp \nonumber \]
Let’s try a harder one! Consider 402 : 3. Here’s the picture:

We are still looking for groups of three dots: 
There is certainly one group at the 100’s level.
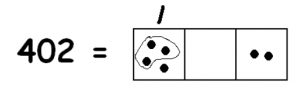
and now it seems we are stuck there are no more groups of three!
What can we do now? Are we really stuck? Can you finish the division problem?
Here are the details worked out for 402 : 3. But don’t read this until you’ve thought about it yourself!
Since each dot is worth ten dots in the box to the right we can write:
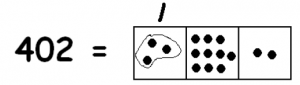
Now we can find more groups of three:
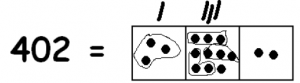
There is still a troublesome extra dot. Let’s unexplode it too
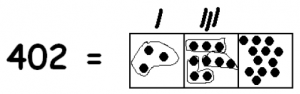
This gives us more groups of three:
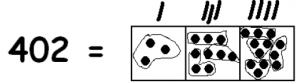
In the picture we have:
- One group of 3 in the hundreds box.
- Three groups of 3 in the tens box.
- Four groups of 3 in the ones box.
Finally we have the answer!
\[402 \div 3 = 134 \ldotp \nonumber \]
Solve each of these exercises using the dots and boxes method:
\[62124 : 3 \qquad \qquad 61230 : 5 \nonumber \]
Let’s turn up the difficulty a notch. Consider 156 : 12. Here we are looking for groups of 12 in this picture:
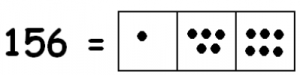
What does 12 look like? It can be twelve dots in a single box:
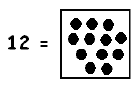
But most often we would write 12 this way, as a ten and 2 ones:
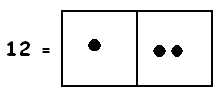
We certainly see some of these in the picture. There is certainly one at the tens level:
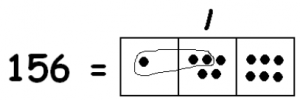
Note: With an unexplosion this would be twelve dots in the tens box, so we mark one group of 12 above the tens box.
We also see three groups of twelve ones:
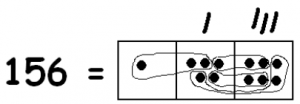
So in the picture we have:
- One group of 12 dots in the tens box.
- Three groups of 12 dots in the ones box.
That means
\[156 : 12 = 13 \ldotp \nonumber \]
Use the dots and boxes model to compute each of the following:
\[\begin{split} 13453 & : 11 \\ 4853 & : 23 \\ 214506 & : 102 \end{split} \nonumber \]
Remember that base five numbers are in a 1 ← 5 dots-and-boxes system. What are the place values in the 1 ← 5 system? Fill in the blanks:
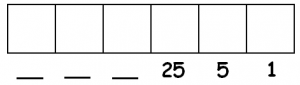
- Draw a dots-and-boxes picture of the number \(424_{five}\).
- Draw a dots-and-boxes picture of the number \(11_{five}\).
- Use the dots and boxes method to find \(424_{five} \div 11_{five}\).
- Rewrite the division sentence \(424_{five} \div 11_{five} = 34_{five}\) in base ten, and check that it’s correct.
- Use dots-and-boxes to find \(2021_{five} \div 12_{five}\). Don’t convert to base 10!
- Use dots and boxes to compute these. $$\begin{split} 2130 & :10 \\ 41300 & : 100 \end{split}$$
- What pictures did you use for 10 and for 100? Can you describe in words what happens when dividing by 10 and by 100 and why?
The Standard Algorithm for Division
We used dots and boxes to show that 402 : 3 = 134.

In elementary school, you might have learned to solve this division problem by using a diagram like the following:
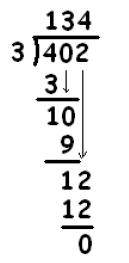
At first glance this seems very mysterious, but it is really no different from the dots and boxes method. Here is what the table means.
To compute 402 : 3, we first make a big estimation as to how many groups of 3 there are in 402. Let’s guess that there are 100 groups of three.
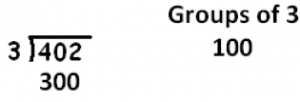
How much is left over after taking away 100 groups of 3? We subtract to find that there is 102 left.

How many groups of 3 are in 102? Let’s try 30:
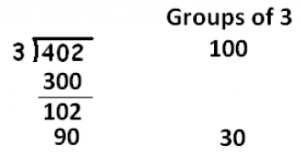
How many are left? There are 12 left and there are four groups of 3 in 12.
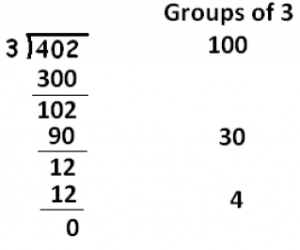
That accounts for entire number 402. And where do we find the final answer? Just add the total count of groups of three that we tallied:
\[402 : 3 = 100 + 30 + 4 = 134 \ldotp \nonumber \]
- Compare the two division diagrams below. In what way are they the same? In what way are they different?
- Also look at the dots and boxes method. In what way is it the same or different from the two diagrams?



- Why do we like the standard algorithm? Because it is quick, not too much to write down, and it works every time.
- Why do we like the dots and boxes method? Because it easy to understand. (And drawing dots and boxes is kind of fun!)
Division with Remainders
We saw that 402 is evenly divisible by 3: 402 : 3 = 134. This means that 403, one more, shouldn’t be divisible by three. It should be one dot too big.
Do we see the extra dot if we compute 402 : 3 with dots and boxes?
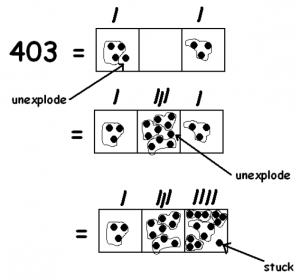
Yes we do! We have one dot left at the end that can’t be divided. This is how it looks in the standard algorithm.
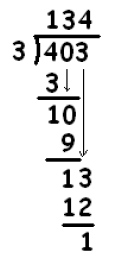
In school, we say that we have a remainder of one and sometimes write:
\[403 \div 3 = 134\; \text{R} 1 \ldotp \nonumber \]
But what does that really mean? It means that we have 134 groups of three with one dot left over. So
\[402 = 134 \cdot 3 + 1 \ldotp \nonumber \]
Let’s try another one: 263 ÷ 12. Here’s what we have:
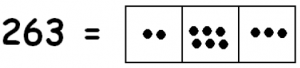
And we are looking for groups like this:

Here goes!
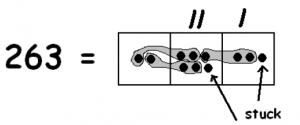
Unexploding won’t help any further and we are indeed left with one remaining dot in the tens position and a dot in the ones position. We have 21 groups of twelve, and a remainder of eleven.
\[263 = 21 \cdot 12 + 11 \ldotp \nonumber \]
- Use the dots and boxes method to compute each quotient and remainder: $$\begin{split} 5210 & : 4 \\ 4857 & : 23 \\ 31533 & : 101 \end{split}$$
- Now use the standard algorithm (an example is shown below) to compute each of the quotients and remainders above.
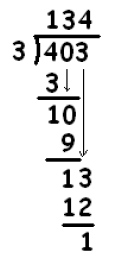
\[402 = 134 \cdot 3 + 1 \ldotp \nonumber \]
- Which method do you like better: dots and boxes or the standard algorithm method? Or does it depend on the problem you are doing?


