6.4: Division and Decimals
- Page ID
- 9859
When you studied fractions, you had lots of different ways to think about them. But the first way, and the one we keep coming back to, is to think of a fraction as the answer to a division problem.
Suppose 6 pies are to be shared equally among 3 children. This yields 2 pies per child. We write:
\[\frac{6}{3} = 2 \ldotp \nonumber \]
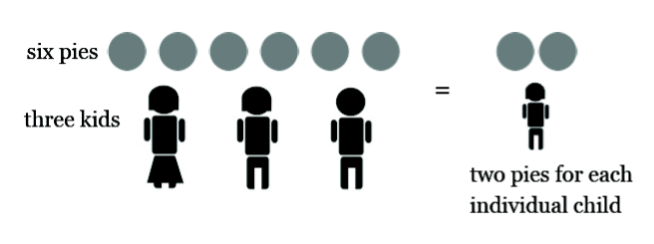
The fraction \(\frac{6}{3}\) is equivalent to the answer to the division problem \(6 \div 3 = 2\). It represents the number of pies one whole child receives.
In the same way…
sharing 10 pies among 2 kids yields \(\frac{10}{2} = 5\) pies per kid,
sharing 8 pies among 2 kids yields \(\frac{8}{2} = 4\) pies per kid,
sharing 5 pies among 5 kids yields \(\frac{5}{5} = 1\) pies per kid, and
the answer to sharing 1 pies among 2 children is \(\frac{1}{2}\), which we call “one-half.”
We associate the number “\(\frac{1}{2}\)” to the picture  .
.
In the same way, the picture  represents “one third,” that is, \(\frac{1}{5}\).
represents “one third,” that is, \(\frac{1}{5}\).
(This is the amount of pie an individual child would receive if one pie is shared among three children.)
The picture  is called “one fifth” and is indeed \(\frac{1}{5}\), the amount of pie an individual child receives when one pie is shared by five kids.
is called “one fifth” and is indeed \(\frac{1}{5}\), the amount of pie an individual child receives when one pie is shared by five kids.
And the picture  is called “three fifths” to represent \(\frac{3}{5}\), the amount of pie an individual receives if three pies are shared by five kids.
is called “three fifths” to represent \(\frac{3}{5}\), the amount of pie an individual receives if three pies are shared by five kids.
We know how to do division in our “Dots & Boxes” model.
Suppose you are asked to compute \(3906 \div 3\). One way to interpret this question (there are others) is:
“How many groups of 3 fit into 3906?”
In our “Dots & Boxes” model, the dividend 3906 looks like this:
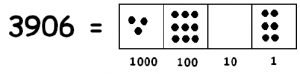
and three dots looks like this: 
So we are really asking:
“How many groups of  fit into the picture of 3906?”
fit into the picture of 3906?”
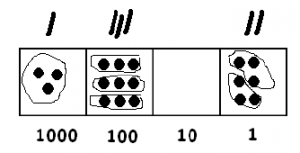
Notice what we have in the picture:
- One group of 3 in the thousands box.
- Three groups of 3 in the hundreds box.
- Zero groups of 3 in the tens box.
- Two groups of 3 in the ones box.
This shows that 3 goes into 3906 one thousand, three hundreds and two ones times. That is,
\[3906 \div 3 = 1302 \ldotp \nonumber \]
Of course, not every division problem works out evenly! Here’s a different example.
Suppose you are asked to compute \(1024 \div 3\). One way to interpret this question is:
“How many groups of 3 fit into 1024?”
So we’re looking for groups of three dots in this picture:
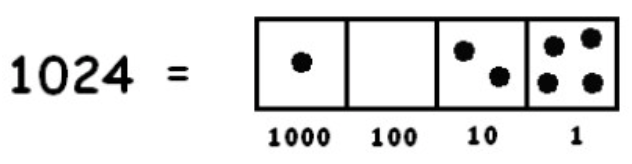
One group of three is easy to spot:
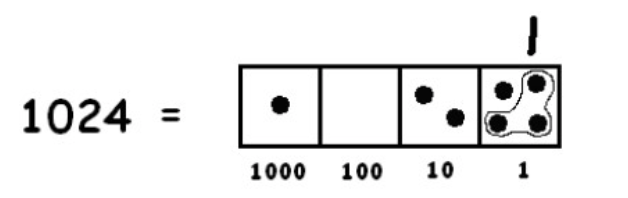
To find more groups of three dots, we must “unexplode” a dot:
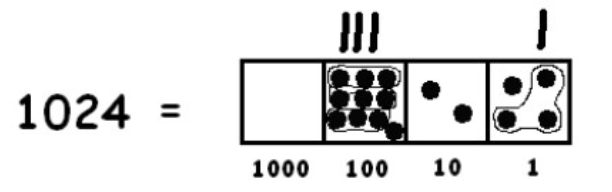
We need to unexplode again:
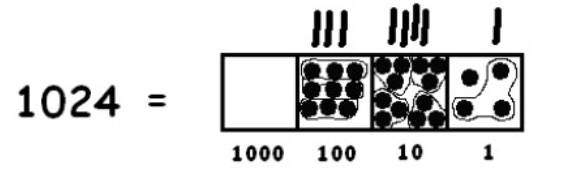
This leaves one stubborn dot remaining in the ones box and no more group of three. So we conclude:
\[1024 \div 3 = 341\; \text{R} 1,\; meaning\; 1024 = 341 \cdot 3 + 1 \ldotp \nonumber \]
In words: 1024 gives 341 groups of 3, plus one extra dot.
We can put these two ideas together — fractions as the answer to a division problem and what we know about division in the “Dots & Boxes” model — to help us think more about the connection between fractions and decimals.
The fraction \(\frac{1}{8}\) is the result of dividing 1 by 8. Let’s actually compute \(1 \div 8\) in a “Dots & Boxes” model, making use of decimals. We want to find groups of eight in the following picture:
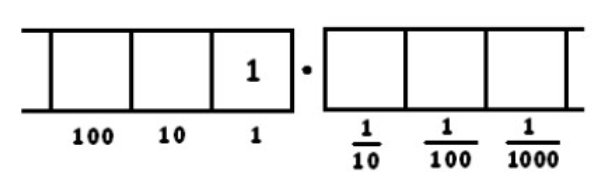
Clearly none are to be found, so let’s unexplode:
(We’re being lazy and not drawing all the dots. As you follow along, you might want to draw the dots rather than the number of dots, if it helps you keep track.)
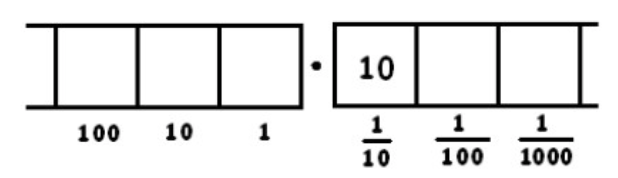
Now there is one group of 8, leaving two behind. We write a tick-mark on top, to keep track of the number of groups of 8, and leave two dots behind in the box.
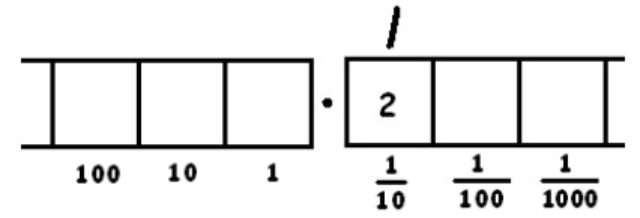
We can unexplode the two dots in the \(\frac{1}{10}\) box:
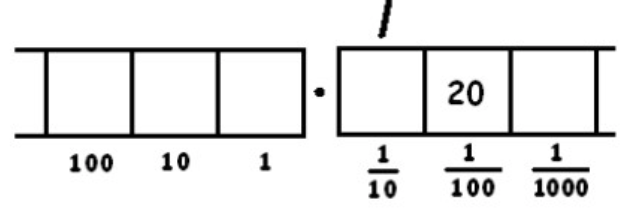
This gives two groups of 8 leaving four behind. Remember: the two tick marks represent two groups of 8. And there are four dots left in the \(\frac{1}{100}\) box.
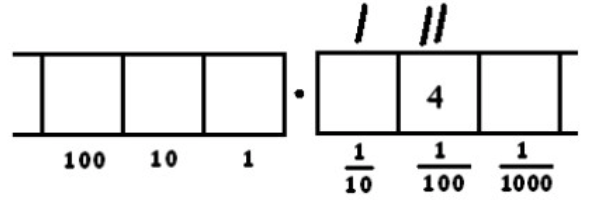
Unexploding those four remaining dots:
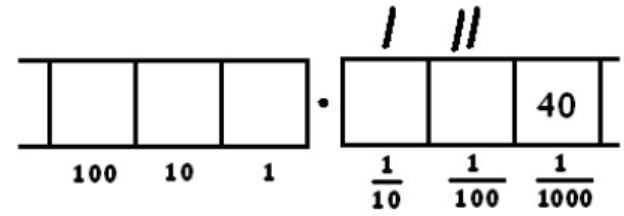
Now we have five groups of 8 and no remainder.
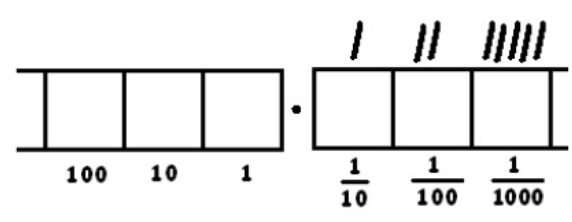
Remember: the tick marks kept track of how many groups of eight there were in each box. We have
- One group of 8 dots in the \(\frac{1}{10}\) box
- Two groups of 8 dots in the \(\frac{1}{100}\) box.
- Five groups of 8 dots in the \(\frac{1}{1000}\) box.
So we conclude that:
\[\frac{1}{8} = 1 \div 8 = 0.125 \ldotp \nonumber \]
Of course, it’s a good habit to check our answer:
\[0.125 = \frac{125}{1000} = \frac{5 \cdot 25}{5 \cdot 200} = \frac{5 \cdot 5}{5 \cdot 40} = \frac{5 \cdot 1}{5 \cdot 8} = \frac{1}{8} \ldotp \nonumber \]
On Your Own
Work on the following exercises on your own or with a partner. Be sure to show your work.
- Perform the division in a “Dots & Boxes” model to show that \(\frac{1}{4}\), as a decimal, is \(0.25\).
- Perform the division in a “Dots & Boxes” model to show that \(\frac{1}{2}\), as a decimal, is \(0.5\).
- Perform the division in a “Dots & Boxes” model to show that \(\frac{3}{5}\), as a decimal, is \(0.6\).
- Perform the division in a “Dots & Boxes” model to show that \(\frac{3}{6}\), as a decimal, is \(0.1875\).
- In simplest terms, what fraction is represented by each of these decimals? $$0.75, \qquad 0.625, \qquad 0.16, \qquad 0.85, \qquad 0.0625 \ldotp$$
Repeating Decimals
Not all fractions lead to simple decimal representations.
Consider the fraction \(\frac{1}{3}\). We seek groups of three in the following picture:
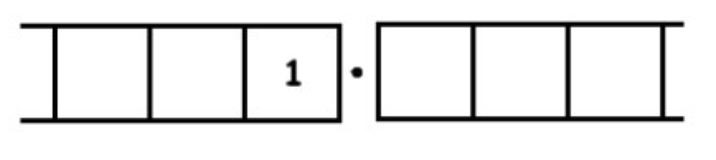
Unexploding requires us to look for groups of 3 in:
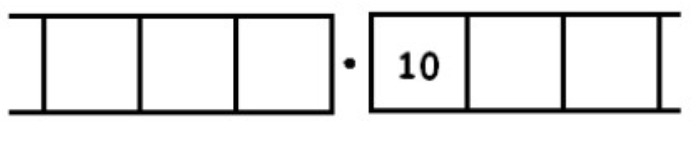
Here there are three groups of 3 leaving one behind:
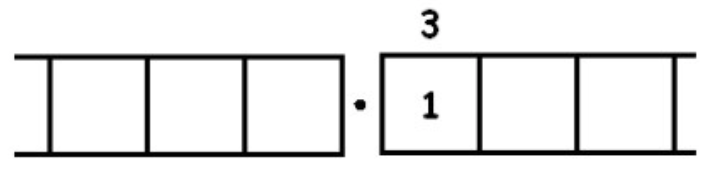
Unexploding gives:
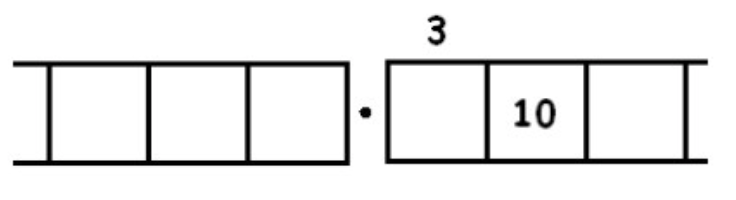
We find another three groups of 3 leaving one behind:
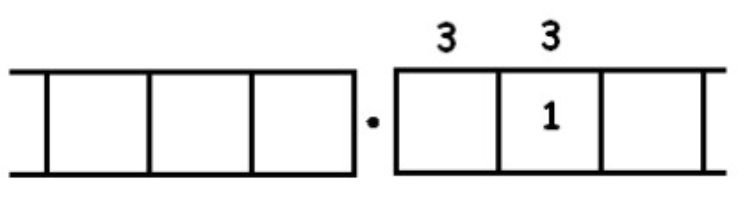
Unexploding gives:
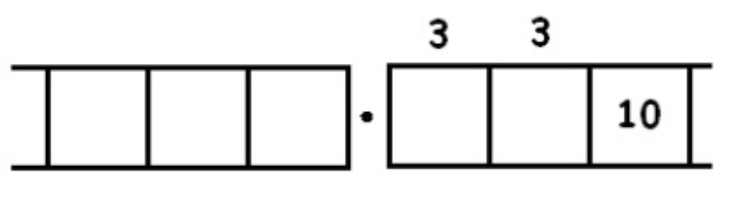
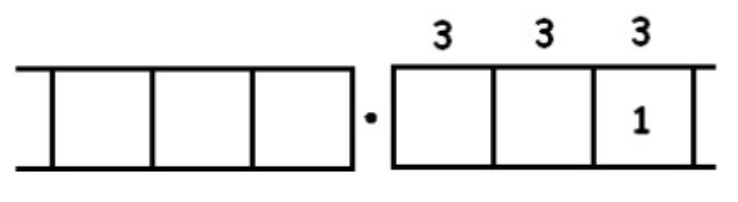
And we seem to be caught in an infinitely repeating cycle.
We are now in a philosophically interesting position. As human beings, we cannot conduct this, or any, activity an infinite number of times. But it seems very tempting to write:
\[\frac{1}{3} = 0.33333 \ldots, \nonumber \]
with the ellipsis “” meaning “keep going forever with this pattern.” We can imagine what this means, but we cannot actually write down those infinitely many 3’s represented by the
Many people make use of a vinculum (horizontal bar) to represent infinitely long repeating decimals. For example, \(0. \bar{3}\) means “repeat the 3 forever”:
\[0. \bar{3} = 0.33333 \ldots, \nonumber \]
and \(0.296 \overline{412}\) means “repeat the 412 forever”:
\[0.296 \overline{412} = 0.296412412412412 \ldots \nonumber \]
Now we’re in a position to give a perhaps more satisfying answer to the question \(1024 \div 3\). In the example above, we found the answer to be
\[1024 \div 3 = 341\; \text{R} 1 \ldotp \nonumber \]
But now we know we can keep dividing that last stubborn dot by 3. Remember, that represents a single dot in the ones place, so if we keep dividing by three it really represents \(\frac{1}{3}\). So we have:
\[1024 \div 3 = 341\; \text{R} 1 = 341 \frac{1}{3} = 341.3333333 \ldots = 341. \bar{3} \ldotp \nonumber \]
As another (more complicated) example, here is the work that converts the fraction \(\frac{6}{7}\) to an infinitely long repeating decimal. Make sure to understand the steps one line to the next.
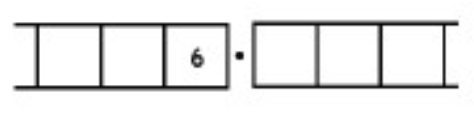
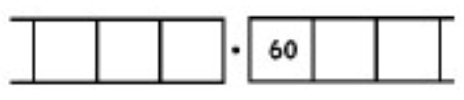
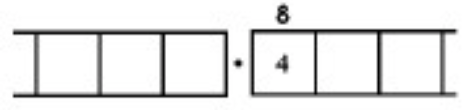
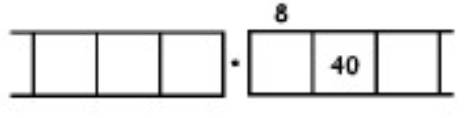
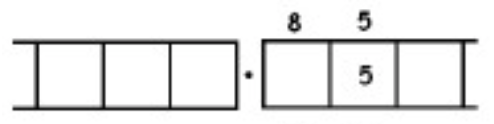
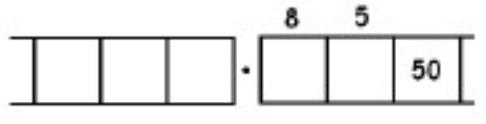
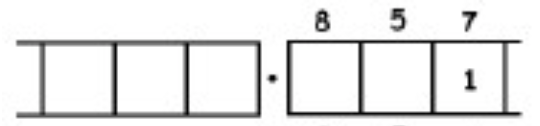
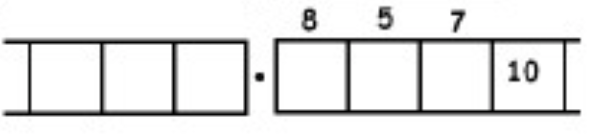
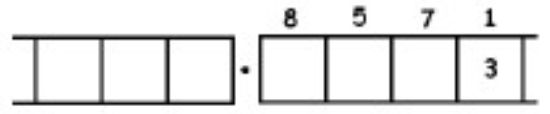
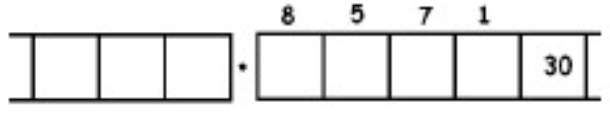


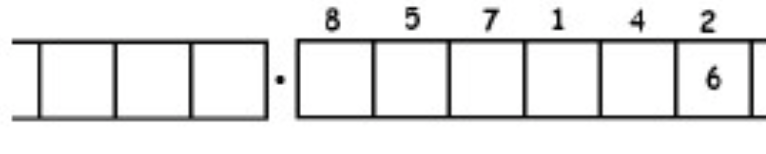
With this 6 in the final right-most box, we have returned to the very beginning of the problem. (Do you see why? Remember, we started with a six in the ones box!)
This means that we will simply repeat the work we have done and obtain the same sequence of answers: \(857142\). And then again, and then again, and then again. We have:
\[\begin{split} \frac{6}{7} &= 0.857142857142857142857142 \ldots \\ &= 0. \overline{857142} \ldotp \end{split} \nonumber \]
On Your Own
Work on the following exercises on your own or with a partner. Be sure to show your work.
- Compute \(\frac{4}{7}\) as an infinitely long repeating decimal.
- Compute \(\frac{1}{9}\) as an infinitely long repeating decimal.
- Use a “Dots & Boxes” model to compute \(133 \div 6\). Write the answer as a decimal.
- Use a “Dots & Boxes” model to compute \(255 \div 11\). Write the answer as a decimal.


