11.1: Fundamentals of Annuities

Last updated
Save as PDF

Page ID: 22131

Jean-Paul Olivier
Red River College of Applied Arts, Science, & Technology

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

It is impossible to calculate payments accurately until you recognize a few of the key characteristics illustrated in the chapter introduction:

All of the examples required a payment in the same amount on a regular basis, such as the $872.41 every month for your mortgage.
The timing of the payments varied. The car lease required the first payment up front (at the beginning of the month), while the mortgage and mattress purchase had the first payment due a month after the purchase (at the end of the month).
The frequency of the payments and the frequency of the interest rate varied. The mortgage had monthly payments with interest being charged semi-annually, while the car lease had monthly payments and monthly interest.

Unlike single payments (covered in Chapter 9) for which there is only one formula, you solve series of payments by choosing the appropriate formula from four possibilities defined by the financial characteristics of the payments. This section defines the characteristics of four different types of payment series and then contrasts them to the Chapter 9 and Chapter 10 single payment calculations. This section also develops a new, simplified structure for timelines to help you visualize a series of payments.

What Are Annuities?

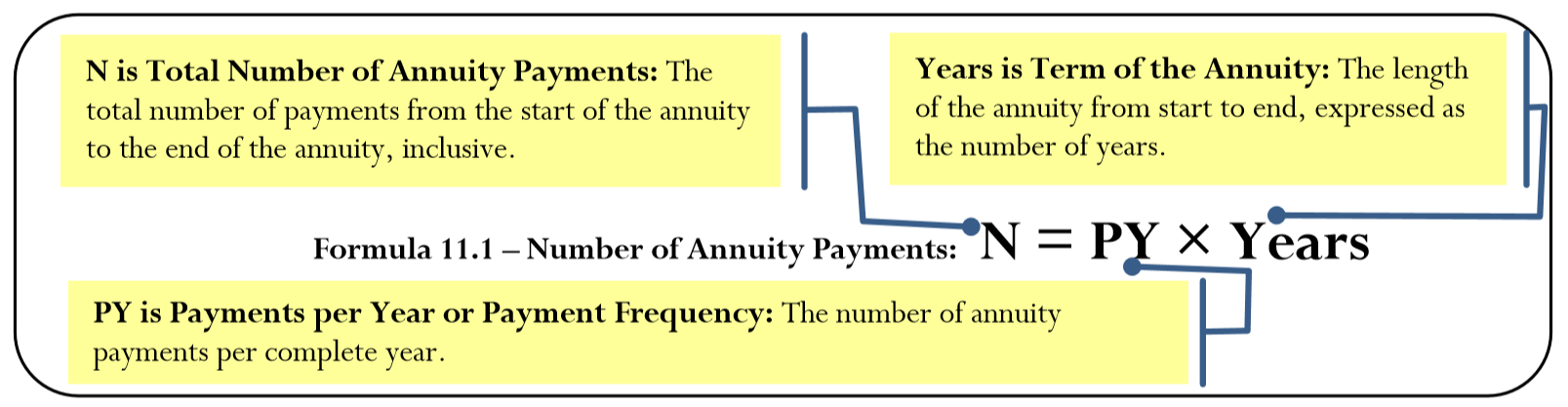
An annuity is a continuous stream of equal periodic payments from one party to another for a specified period of time to fulfill a financial obligation. An annuity payment is the dollar amount of the equal periodic payment in an annuity environment. The figure below illustrates a six-month annuity with monthly payments. Notice that the payments are continuous, equal, periodic, and occur over a fixed time frame. If any one of these four characteristics is not satisfied, then the financial transaction fails to meet the definition of a singular annuity and requires other techniques and formulas to solve.

$clipboard_e554f8d5c481e045024b7d25b08ae4e8a.png$

The examples below illustrate four timelines that look similar to the one above, but with one of the characteristics of an annuity violated. This means that none of the following in their entirety are considered an annuity:

Continuous. Annuity payments are without interruption or breaks from the beginning through to the end of the annuity's term. In the figure above there are no breaks in the annuity since every month has an annuity payment. This next figure is not an annuity because the absence of a payment in the third month makes the series of payments discontinuous.

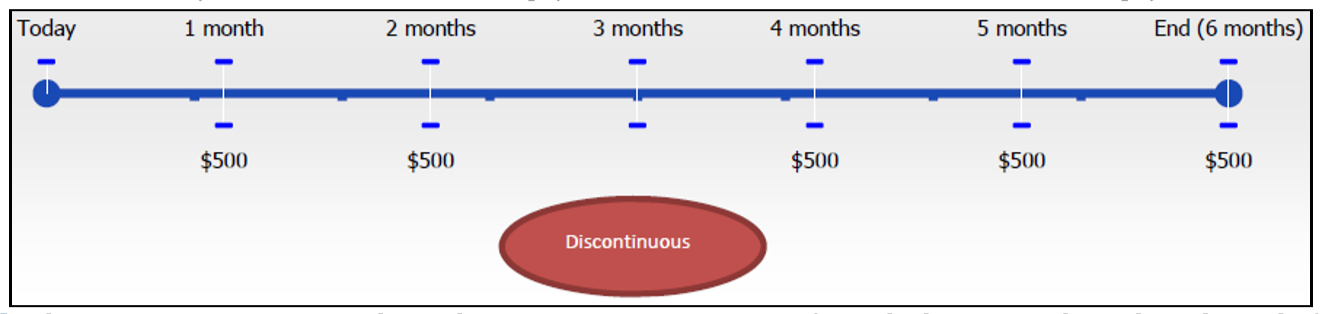
$clipboard_eaf71a2a3b3063170b5eefdf74f06a7e1.png$

Equal. The annuity payments must be in the same amount every time from the beginning through to the end of the annuity's term. In the original figure, every monthly annuity is $500. Notice that in this next figure the payment amount varies and includes values of both $500 and $600.

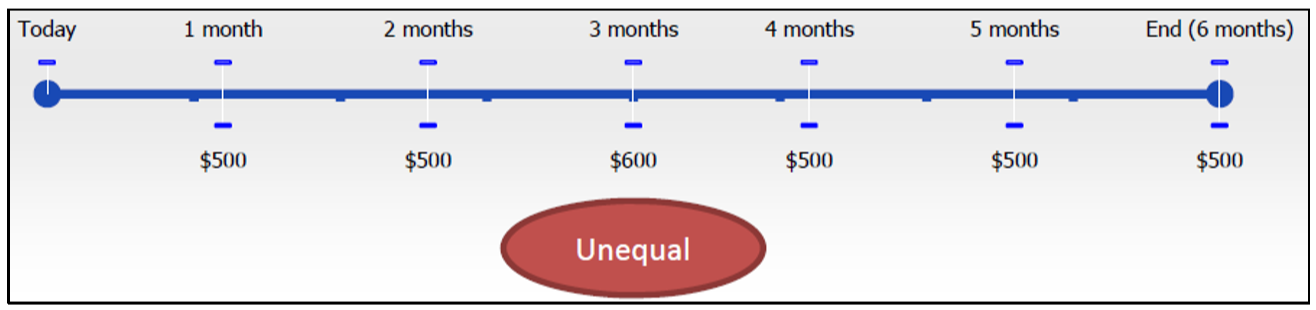
$clipboard_ea4de913d6be6d3922284947a8b3c38da.png$

Periodic. The amount of time between each continuous and equal annuity payment is known as the payment interval. Hence, a monthly payment interval means payments have one month between them, whereas a semi-annual payment interval means payments have six months between them. Annuity payments must always have the same payment interval from the beginning through to the end of the annuity's term. In the original figure there is exactly one month between each equal and repeated payment in the annuity. Notice that in this next figure the payments, although equal and continuous, do not occur with the same amount of time between each one. In fact, the first three payments are made monthly while the last three payments are made quarterly. (You may notice that if the first three payments are treated separately from the last three payments, then each separate grouping represents an annuity and therefore there are two separate annuities. However, as a whole this is not an annuity.)

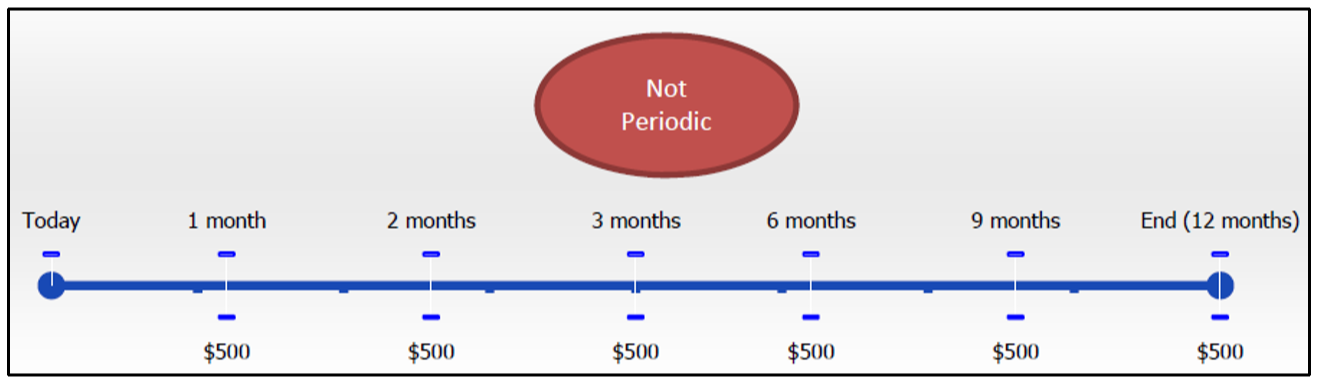
$clipboard_e9f85edae5cabfc59103ffc8fd03f88ef.png$

Specified Period of Time. The annuity payments must occur within an identifiable time frame that has a specified beginning and a specified end. The annuity's time frame can be (1) known with a defined starting date and defined ending date, such as the annuity illustrated in the original figure, which endures for six periods; (2) known but nonterminating, such as beginning today and continuing forever into the future (hence an infinite period of time); or (3) unknown but having a clear termination point, for example, monthly pension payments that begin when you retire and end when you die—a date that is obviously not known beforehand. In the next figure, the annuity has no defined ending date, does not continue into the future, and no clear termination point is identifiable.

$clipboard_ee238a31868aa3623ab266b02028f4666.png$

In summary, the first figure is an annuity that adheres to all four characteristics and can be addressed via an annuity formula. The next four figures are not annuities and need other financial techniques or formulas to perform any necessary calculations.

Types of Annuities

There are four types of annuities, which are based on the combination of two key characteristics: timing of payments and frequency. Let’s explore these characteristics first, after which we will discuss the different annuity types.

Timing of Payments. An example best illustrates this characteristic. Assume that you take out a loan today with monthly payments. If you were to make your first annuity payment on the day you take out the loan, the amount of principal owing would be immediately reduced and you would accumulate a smaller amount of interest during your first month. This is called making your annuity payment at the beginning of a payment interval, and this payment is known as a due. However, if a month passes before you make your first monthly payment on the loan, your original principal accumulates more interest than if the principal had already been reduced. This is called making your payment at the end of the payment interval, and this payment is known as an ordinary because it is the most common form of annuity payment. Depending on when you make your payment, different principal and interest amounts occur.
Frequency. The frequency of an annuity refers to a comparison between the payment frequency and the compounding frequency. A payment frequency is the number of annuity payments that would occur in a complete year. Recall from Chapter 9 that the compounding frequency is the number of compounds per complete year. If the payment frequency is the same as the compounding frequency, this is called a simple annuity. When interest is charged to the account monthly and payments are also made monthly, you determine principal and interest using simplified formulas. However, if the payment frequency and the compounding frequency are different, this is called a general annuity. If, for example, you make payments monthly while interest is compounded semi-annually, you have to use more complex formulas to determine principal and interest since the paying of principal and charging of interest do not occur simultaneously.

Putting these two characteristics together in their four combinations creates the four types of annuities. Each timeline in these figures assumes a transaction involving six semi-annual payments over a three-year time period.

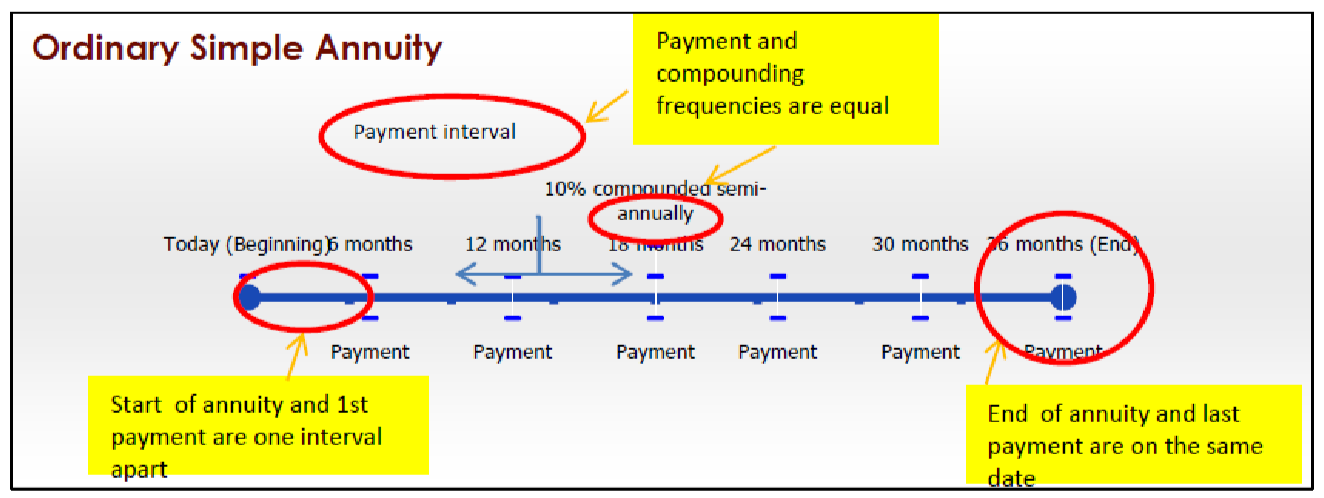
$clipboard_ed515063a3f2494da95647671f5e35dbe.png$

Ordinary Simple Annuity

An ordinary simple annuity has the following characteristics:

Payments are made at the end of the payment intervals, and the payment and compounding frequencies are equal.
The first payment occurs one interval after the beginning of the annuity.
The last payment occurs on the same date as the end of the annuity.

For example, most car loans are ordinary simple annuities where payments are made monthly and interest rates are compounded monthly. As well, car loans do not require the first monthly payment until the end of the first month.

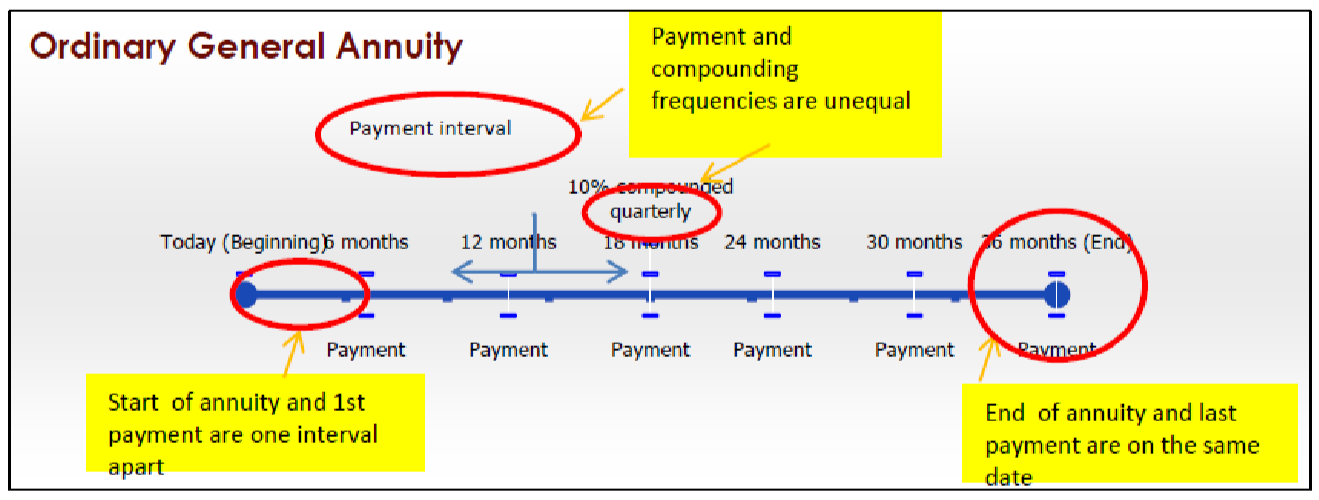
$clipboard_eecdddc770fa7a30e8eb165d3c7e69a7d.png$

Ordinary General Annuity

An ordinary general annuity has the following characteristics:

Payments are made at the end of the payment intervals, and the payment and compounding frequencies are unequal.
The first payment occurs one interval after the beginning of the annuity.
The last payment occurs on the same date as the end of the annuity.

For example, most mortgages are ordinary general annuities, where payments are made monthly and interest rates are compounded semi-annually. As with car loans, your first monthly payment is not required until one month elapses.

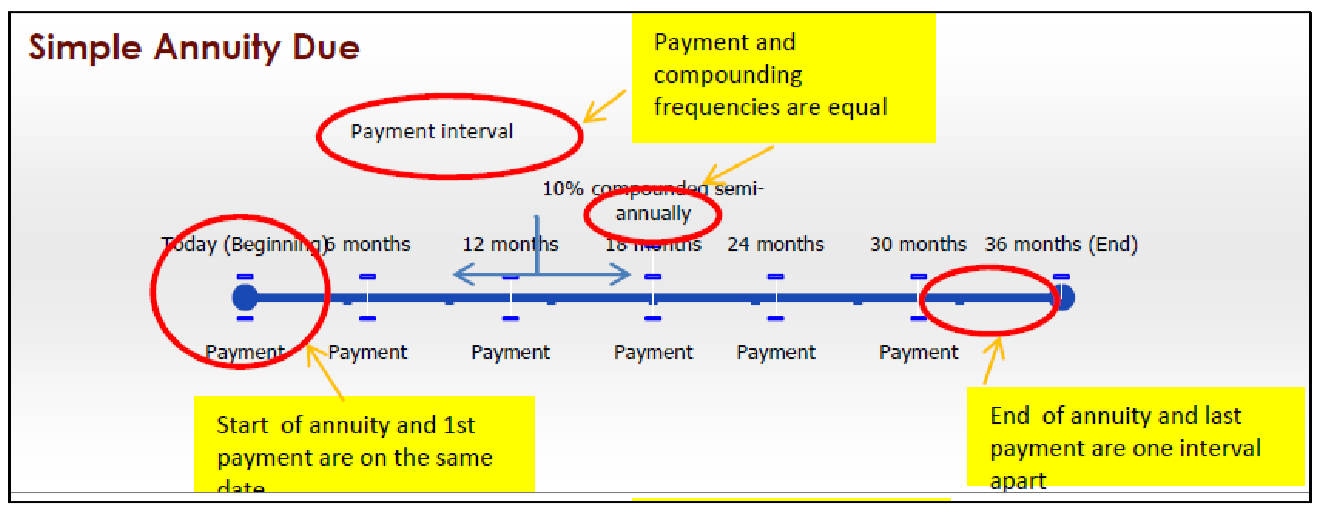
$clipboard_e4261d6176a026de70ada501d33c26522.png$

Simple Annuity Due

A simple annuity due has the following characteristics:

Payments are made at the beginning of the payment intervals, and the payment and compounding frequencies are equal.
The first payment occurs on the same date as the beginning of the annuity.
The last payment occurs one payment interval before the end of the annuity.

For example, most car leases are simple annuities due, where payments are made monthly and interest rates are compounded monthly. However, the day you sign the lease is when you must make your first monthly payment.

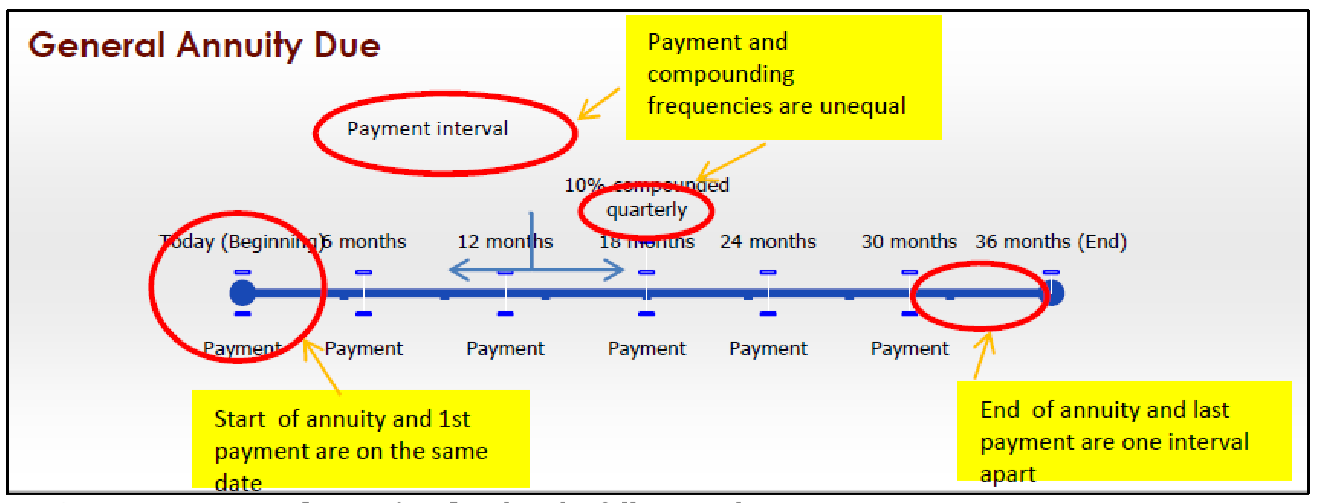
$clipboard_e26d04f5a2f646857c41be019daed72f3.png$

General Annuity Due.

A general annuity due has the following characteristics:

Payments are made at the beginning of the payment intervals, and the payment and compounding frequencies are unequal.
The first payment occurs on the same date as the beginning of the annuity.
The last payment occurs one payment interval before the end of the annuity.

For example, many investments, like your RRSP, are general annuities due where payments (contributions) are typically made monthly but the interest compounds in another manner, such as annually. As well, when most people start an RRSP they pay into it on the day they set it up, meaning that their RRSP commences with the first deposited payment.

The table below summarizes the four types of annuities and their characteristics for easy reference.

Annuity Type	Timing of Payments in a Payment Interval	Payment Frequency and Compounding Frequency	Start of Annuity and First Payment Same Date?	End of Annuity and Last Payment Same Date?
Ordinary Simple Annuity	End	Equal	No, first payment one interval later	Yes
Ordinary General Annuity	End	Unequal	No, first payment one interval later	Yes
Simple Annuity Due	Beginning	Equal	Yes	No, last payment one interval earlier
General Annuity Due	Beginning	Unequal	Yes	No, last payment one interval earlier

Paths To Success

One of the most challenging aspects of annuities is recognizing whether the annuity you are working with is ordinary or due. This distinction plays a critical role in formula selection later in this chapter. To help you recognize the difference, the table below summarizes some key words along with common applications in which the annuity may appear.

Type	Key Words or Phrases	Common Applications
Ordinary	-... payments are at the end.... -... payments do not start today... -... payments are later... -... first payment next interval...	- bank loans of any type - mortgages - bonds - Canada Pension Plan (CPP)
Due	-...payments are at the beginning... -...payments start today... -... payments are in advance... -...first payment today... -...payments start now...	- any kind of lease - any kind of rental - RRSPs (usually) - membership dues - insurance

Annuities versus Single Payments

To go from single payments in Chapter 9 to annuities in this chapter, you need to make several adaptations:

Annuity Payment Amount (PMT). This variable was not used in any of the formulas introduced in Chapter 9 or Chapter 10, though it was briefly introduced when Section 9.2 when demonstrating the calculator functions. Notice that in the previous two chapters this variable was set to zero for every question, since every payment was not part of an annuity. Annuity calculations require you to tie a value to this variable in the formulas and when you use technology such as the BAII+ calculator.
Payment Frequency or Payments per Year (PY). For single payments, this variable did not show up in any of the formulas from the previous two chapters. It too was introduced in Section 9.2 as a calculator button with the requirement that it automatically be set as a null variable matching the compounding frequency (CY). When you work with annuities, an actual value for $PY$ is determined by the payment frequency. For simple annuities $PY$ remains the same as $CY$, whereas the variables are different for general annuities.
Cash Flow Sign Convention on the Calculator. It now becomes critical to ensure the proper application of the cash flow sign convention on the calculator—failure to do so will result in an incorrect answer. For example, if you borrow money and then make annuity payments on it, you enter the present value ($PV$) as a positive (you received the money) while you enter the annuity payments as negatives (you paid the money to the bank). This results in future balances getting smaller and you owing less money. If you inadvertently enter the annuity payment as a positive number, this would mean you are borrowing more money from the bank so your future balance would increase and you would owe more money. These two answers are very different!
Definition and Computation of N. When you worked with single payments, $N$ was defined as the total number of compounds throughout the term of the financial transaction. When you work with annuities, $N$ is defined as the total number of payments throughout the term of the annuity. You calculate it using Formula 11.1.

The Formula

$clipboard_e3982a10b50df004be3651e1a0b8b9776.png$

Formula 11.1

How It Works

On a two-year loan with monthly payments and semi-annual compounding, the payment frequency is monthly, or 12 times per year. With a term of two years, that makes N = 2 × 12 = 24 payments. Note that the calculation of N for an annuity does not involve the compounding frequency.

Adapting Timelines to Incorporate Annuities

Annuity questions can involve many payments. For example, in a typical 25-year mortgage with monthly payments, that would be 25 × 12 = 300 payments in total. How would you draw a timeline for these? Clearly, it would be impractical to draw 300 payments.

A good annuity timeline should illustrate the present value ($PV$), future value ($FV$), number of annuity payments ($N$), nominal interest rate ($IY$), compounding frequency ($CY$), annuity payment ($PMT$), and the payment frequency ($PY$). One of these variables will be the unknown.

As well, a good timeline requires a clear distinction between ordinary annuities and annuities due. END is used to represent ordinary annuities, since payments occur at the end of the payment interval. Similarly, BGN is used to represent annuities due, since payments occur at the beginning of the payment interval. The figure below illustrates the adapted annuity timeline format.

$clipboard_e16e2147badf8e54f249103053c617a54.png$

Sometimes a variable will change partway through the period of an annuity, in which case the timeline must be broken up into two or more segments. When you use this structure, in any time segment the annuity payment $PMT$ is interpreted to have the same amount at the same payment interval continuously throughout the entire segment. The number of annuity payments $N$ does not directly appear on the timeline since it is the result of a formula. However, its two components (Years and PY) are drawn on the timeline.

How It Works

A mortgage is used to illustrate this new format. For now, focus strictly on the variables and how to illustrate them in a timeline. Do not focus on any mortgage calculations yet.

As per the chapter introduction, you purchased a $150,000 home ($PV$) with a 25-year mortgage (Years). The mortgage rate is 5% ($IY$) compounded semi-annually ($CY$ = 2), and the monthly payments ($PY$ = 12) are $872.41 ($PMT$).
After 25 years you will own your house and therefore have no balance remaining. This sets the future value to $0 ($FV$).
Mortgages are ordinary in nature, meaning that payments occur at the end of the payment intervals (END). The figure below places all of these mortgage elements into the new timeline format. Once you have drawn the timeline, you can determine the following:

$clipboard_e91ba49fb9126eb6eda5eb3ae7f588d73.png$

The number of payments ($N$), which you calculate using Formula 11.1. Since both $PY$ and Years are known, you have $N$ = 25 × 12 = 300.
Whether the annuity is simple or general, which depends on the $PY$ below the timeline and $CY$ above the timeline. If they match, the annuity is simple; if they differ, as in this example, it is general.

Things To Watch Out For

The word "payment" often confuses people because it has two interpretations. It could mean either "single payment," such as in Chapter 9, or "annuity payment," which is meant in this chapter. To correctly interpret this word, recall the characteristics of an annuity payment and determine if the situation at hand matches the criteria. Let’s review two examples illustrating this point:

Suppose John owes Mary three payments of $200 due two months, five months, and eleven months from now. In this case, the word "payment" means "single payment" because the payments are equal (all $200) and the time periods are known, but they are neither periodic (payment intervals are unequal) nor continuous (since no periods exist, there is no continuity). Working with these payments requires you to apply the formulas and techniques from Chapter 9.
Suppose John owes Julia three payments of $200 due three months, six months, and nine months from now. In this case, the word "payment" means "annuity payment" because the payments are equal (all $200), periodic (every quarter), and continuous (occurring every quarter without interruption), and they have a specified time frame (over nine months). Working with these payments allows you to apply the formulas and techniques from this chapter.

Ultimately, when in doubt you can solve any question involving time value of money using the formulas and techniques from Chapter 9. The annuity formulas introduced in the next section just allow you to arrive at the same answer with a lot less calculation.

Contributors and Attributions

Template:ContribBusiMathOlivier

Search

Text Color

Text Size

Margin Size

Font Type