9.3: Measuring Volume
- Page ID
- 129629
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify reasonable values for volume applications.
- Convert between like units of measures of volume.
- Convert between different unit values.
- Solve application problems involving volume.
Volume is a measure of the space contained within or occupied by three-dimensional objects. It could be a box, a pool, a storage unit, or any other three-dimensional object with attributes that can be measured in the metric unit for distance–meters. For example, when purchasing an SUV, you may want to compare how many cubic units of cargo the SUV can hold.
Cubic units indicate that three measures in the same units have been multiplied together. For example, to find the volume of a rectangular prism, you would multiply the length units by the width units and the height units to determine the volume in square units:
Note that to accurately calculate volume, each of the measures being multiplied must be of the same units. For example, to find a volume in cubic centimeters, each of the measures must be in centimeters.
The formula used to determine volume depends on the shape of the three-dimensional object. Here we will limit our discussions to the area to rectangular prisms like the one in Figure 9.9 Given this limitation, the basic formula for volume is:
Reasonable Values for Volume
Because volume is determined by multiplying three lengths, the magnitude of difference between different cubic units is exponential. In other words, while a meter is 100 times greater in length than a centimeter, a cubic meter, m3, is times greater in area than a cubic centimeter, cm3. This relationship between benchmark metric volume units is shown in the following table.
| Units | Relationship | Conversion Rate |
|---|---|---|
| km3 to m3 | 1 km3 = 1,000,000,000 m3 | |
| m3 to dm3 | 1 m3 = 1,000 dm3 | |
| dm3 to cm3 | 1 cm3 = 1,000 dm3 | |
| cm3 to mm3 | 1 cm3 = 1,000 mm3 |
To have an essential understanding of metric volume, you must be able to identify reasonable values for volume. When testing for reasonableness you should assess both the unit and the unit value. Only by examining both can you determine whether the given volume is reasonable for the situation.
A grandparent wants to send cookies to their grandchild away at college. Which represents a reasonable value for the volume of a box to ship the cookies:
- 3,375 km3,
- 3,375 m3, or
- 3,375 cm3?
- Answer
-
A volume of 3,375 km3 is equivalent to a rectangular prism with dimensions of which is far too large for a shipping box. An area of 3,375 m3 is equivalent to a surface of which is also too large. A reasonable value for the volume of the box is 3,375 cm3.
8 m3, 8 cm3, or 8 mm3?
A food manufacturer is prototyping new packaging for one of its most popular products. Which represents a reasonable value for the volume of the box:
- 2 dm3,
- 2 cm3, or
- 2 mm3?
- Answer
-
A decimeter is equal to 10 centimeters. A box with a volume of 2 dm3 might have the dimensions , or , which is reasonable. A box with a volume of 2 cm3 or 2 mm3 would be too small.
40,000 mm3, 40,000 cm3, or 40,000 m3?
A farmer has a hay loft. They calculate the volume of the hayloft as 64 cm3. Does the calculation make sense? Explain your answer.
- Answer
-
No. Centimeters are used to determine smaller distances, such as the length of a pencil. A hayloft is more than 64 centimeters long, so a more reasonable unit of value would be m2. A volume of 64 m3 can be calculated using the dimensions 4 meters by 4 meters by 4 meters, which are reasonable dimensions for a hayloft. So, a more reasonable value for the volume of the hayloft is 64 m3.
An artist creates a glass paperweight. They decide they want to box and ship the paperweight, so they measure and determine that the volume of the cubic box is 125,000 mm3. Does their calculation make sense? Explain your answer.
Converting Like Units of Measures for Volume
Just like converting units of measure for distance, you can convert units of measure for volume. However, the conversion factor, the number used to multiply or divide to convert from one volume unit to another, is different from the conversion factor for metric distance units. Recall that the conversion factor for volume is exponentially relative to the conversion factor for distance. The most frequently used conversion factors are illustrated in Figure 9.10.
A pencil case has a volume of 1,700 cm3. What is the volume in cubic millimeters?
- Answer
-
Use multiplication to convert from a larger metric volume unit to a smaller metric volume unit. To convert from cm3 to mm3, multiply the value of the volume by 1,000.
The pencil case has a volume of 1,700,000 mm3.
A jewelry box has a volume of 8 cm3. What is the volume of the jewelry box in cubic millimeters?
A shipping container has a volume of 33.2 m3. What is the volume in cubic centimeters?
- Answer
-
Use multiplication to convert a larger metric volume unit to a smaller metric volume unit. To convert from m3 to cm3, first multiply the value of the volume by 1,000 to convert from m3 to dm3, and then multiply again by 1,000 to convert from dm3 to cm3.
The shipping container has a volume of 32,200,000 cm3.
A gasoline storage tank has a volume of 37.854 m3. What is the volume of the storage tank in cubic centimeters?
A holding tank at the local aquarium has a volume of 22,712,000,000 cm3. What is the volume in cubic meters?
- Answer
-
Figure 9.10 indicates that when converting from a smaller metric volume unit to a larger metric volume unit you divide using the given conversion factor. To convert from cm3 to m3, divide the value of the volume by 1,000 to first convert from cm3 to dm3, then divide again to convert from dm3 to m3.
The holding tank has a volume of 22,712 m3.
A warehouse has a volume of 465,000,000 cm3. What is the volume of the warehouse in cubic meters?
Understanding Other Metric Units of Volume
When was the last time you purchased a bottle of soda? Was the volume of the bottle expressed in cubic centimeters or liters? The liter (L) is a metric unit of capacity often used to express the volume of liquids. A liter is equal in volume to 1 cubic decimeter. A milliliter is equal in volume to 1 cubic centimeter. So, when a doctor orders 10 cc (cubic centimeters) of saline to be administered to a patient, they are referring to 10 mL of saline.
The most frequently used factors for converting from cubic meters to liters are listed in Table 9.2.
| m3 to L | m3 to mL |
|---|---|
A holding tank at the local aquarium has a volume of 22,712,000,000 cm3? What is the capacity of the holding tank in liters?
- Answer
-
Use division to convert from cubic centimeters to liters. To determine the equivalent volume in liters, convert from cm3 to L by dividing the value of the volume in cm3 by 1,000.
The holding tank holds 22,712,000 L of water.
A gas can has a volume of 19,000 cm3. How much gas, in liters, does the gas can hold?
An airplane used 150 m3 of fuel to fly from New York to Hawaii. How many liters of fuel did the airplane use?
- Answer
-
Because 1 liter is equivalent to 1 cubic decimeter, use multiplication to convert from m3 to dm3. Multiply the value of the volume by 1,000 to convert from m3 to dm3. Because , the resulting value is equivalent to the number of liters used.
The airplane used 150,000 liters of fuel.
A gasoline storage tank has a volume of 37.854 m3. What is the volume of the storage tank in liters?
How many liters can a pitcher with a volume of 8,000,000 mm3 hold?
- Answer
-
Use division to convert from a smaller metric volume unit to a larger metric volume unit. To convert from mm3 to dm3,
Step 1: Divide by 1,000 to convert from mm3 to cm3.
Step 2: Divide again by 1,000 to convert from cm3 to dm3.
Step 3: Use the unit value to express the volume in terms of liters.
The pitcher can hold 8 liters of liquid.
A glass jar has a volume of 800,000 mm3. How many mL of liquid can the glass jar hold?
Solving Application Problems Involving Volume
Knowing the volume of an object lets you know just how much that object can hold. When making a bowl of punch you might want to know the total amount of liquid a punch bowl can hold. Knowing how many liters of gasoline a car’s tank can hold helps determine how many miles a car can drive on a full tank. Regardless of the application, understanding volume is essential to many every day and professional tasks.
A cubic shipping carton’s dimensions measure . A company wants to fill the carton with smaller cubic boxes that measure . How many of the smaller boxes will fit in each shipping carton?
- Answer
-
Step 1: Determine the volume of the shipping carton.
Step 2: Use the appropriate conversion factor to convert the volume of the shipping carton from m3 to cm3.
Step 3: Determine the volume of the smaller boxes.
Step 4: Divide the volume of the shipping carton, in cm3, by the volume of the smaller box, in cm3.
The shipping carton will hold 8,000 smaller boxes.
A factory can mill 300 cubic meters of flour each day. They package the flour in boxes that measure \(20\,{\text{cm}} \times 5\,{\text{cm}} \times 30\,{\text{cm}}\). How many boxes of flour does the factory produce each day?
A carton of juice measures 6 cm long, 6 cm wide and 20 cm tall. A factory produces 28,800 liters of orange juice each day. How many cartons of orange juice are produced each day?
- Answer
-
Step 1: Find the volume of the carton in cubic centimeters.
Step 2: Convert the volume in cm3 to liters.
Step 3: Divide the number of liters of orange juice produced each day by the volume of each carton.
The factory produces 40,000 cartons of orange juice each day.
An ice cream maker boxes frozen yogurt mix in boxes that measure 25 cm long, 8 cm wide and 35 cm tall. They produce 42,000 liters of frozen yogurt mix each day. How many boxes of frozen yogurt mix are produced each day?
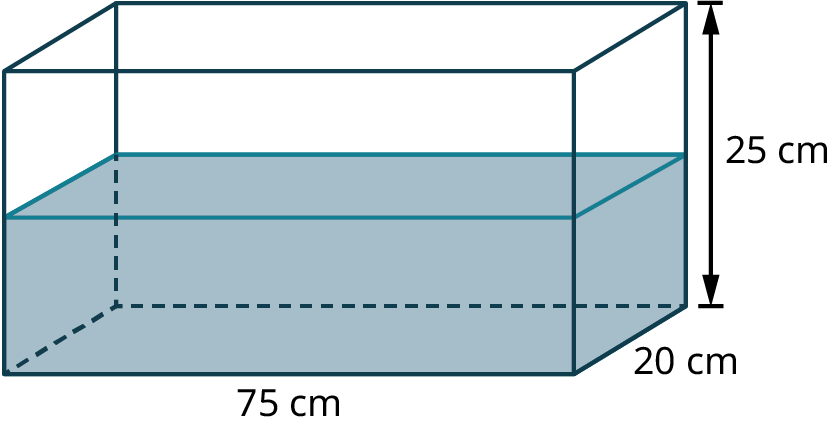
A fish tank measures 60 cm long, 15 cm wide and 34 cm tall (Figure 9.11). The tank is 25 percent full. How many liters of water are needed to completely fill the tank?
- Answer
-
Step 1: Determine the volume of the fish tank in cubic centimeters.
Step 2: Convert the volume in cm3 to volume in liters.
Step 3: Since the tank is 25 percent full, the tank is 75 percent empty. Convert 75 percent to its decimal equivalent. Multiply the total volume by 75 percent expressed in decimal form to determine how many liters of water are required to fill the tank.
So, 22.95 liters of water are needed to fill the tank.
Take two large sheets of card stock. Roll one piece to tape the longer edges together to make a cylinder. Tape the cylinder to the other piece of card stock which serves as the base of the cylinder. Fill the cylinder to the top with cereal. Pour the cereal from the cylinder into a plastic storage or shopping bag. Remove the cylinder from the base and the tape from the cylinder. Re-roll the cylinder along the shorter edges a tape together. Attach the new cylinder to the base. Pour the cereal from the plastic bag into the cylinder. What do you observe? How does the shape of a container affect its volume?
Check Your Understanding
For the following exercises, determine the most reasonable value for each volume.Terrarium: 50,000 km3, 50,000 m3, 50,000 cm3, or 50,000 mm3
Milk carton: 236,000 L, 236 L, 236,000 mL, or 236 mL
Box of crackers: 1,500 km3, 1,500 m3, 1,500 cm3, or 1,500 mm3
For the following exercises, Convert the given volume to the units shown.42,500 mm3 = __________ cm3
1.5 dm3 = __________ mL
6.75 cm3 = __________ mm3
For the following exercises, determine the volume of objects with the dimensions shown.\(V =\) ________ L
\(V =\) ________ mL
\(V =\) ________ m3
Section 9.3 Exercises
For the following exercises, determine the most reasonable value for each volume.71,120 km3, 71,120 m3, 71,120 cm3, or 71,120 mm3
125,000 L, 125 L, 125,000 mL, or 125 mL
2,700 km3, 2,700 m3, 2,700 cm3, or 2,700 mm3
5 L, 0.5 L, 5 mL, or 0.5 mL
3,600 km3, 3.6 m3, 3,600 cm3, or 3,600 mm3
45 L, 45,000 L, 45 mL, or 45,000 mL
\(V =\) ________ L
\(V =\) ________ mL
\(V =\) ________ m3
\(V =\) ________ cm3
\(V =\) ________ m3
\(V =\) ________ L
\(V =\) ________ mL
\(V =\) ________ cm3
\(V =\) ________ m3



