10.7: Area

Last updated
Save as PDF

Page ID: 129645

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

A diagram of a baseball field with its measurements marked. — Figure 10.132: The area of a regulation baseball diamond must adhere to specific measurements to be legal. (credit: "Diagram of Regulation Diamond" by Erica Fischer from "Baseball" The World Book, 1920/Flickr, Public Domain, CC BY 2.0)

Learning Objectives

Calculate the area of triangles.
Calculate the area of quadrilaterals.
Calculate the area of other polygons.
Calculate the area of circles.

Some areas carry more importance than other areas. Did you know that in a baseball game, when the player hits the ball and runs to first base that he must run within a 6-foot wide path? If he veers off slightly to the right, he is out. In other words, a few inches can be the difference in winning or losing a game. Another example is real estate. On Manhattan Island, one square foot of real estate is worth far more than real estate in practically any other area of the country. In other words, we place a value on area. As the context changes, so does the value.

Area refers to a region measured in square units, like a square mile or a square foot. For example, to purchase tile for a kitchen floor, you would need to know how many square feet are needed because tile is sold by the square foot. Carpeting is sold by the square yard. As opposed to linear measurements like perimeter, which in in linear units. For example, fencing is sold in linear units, a linear foot or yard. Linear dimensions refer to an outline or a boundary. Square units refer to the area within that boundary. Different items may have different units, but either way, you must know the linear dimensions to calculate the area.

Many geometric shapes have formulas for calculating areas, such as triangles, regular polygons, and circles. To calculate areas for many irregular curves or shapes, we need calculus. However, in this section, we will only look at geometric shapes that have known area formulas. The notation for area, as mentioned, is in square units and we write sq in or sq cm, or use an exponent, such as ${in}^{2}$ or ${cm}^{2} .$ Note that linear measurements have no exponent above the units or we can say that the exponent is 1.

Area of Triangles

The formula for the area of a triangle is given as follows.

FORMULA

The area of a triangle is given as $A = \frac{1}{2} b h,$ where $b$ represents the base and $h$ represents the height.

For example, consider the triangle in Figure 10.133.

A right triangle with its legs marked 5 centimeters and 4 centimeters. — Figure 10.133: Triangle 1

The base measures 4 cm and the height measures 5 cm. Using the formula, we can calculate the area:

$A = \frac{1}{2} (4) (5) = \frac{1}{2} (20) = 10 {cm}^{2}$

In Figure 10.134, the triangle has a base equal to 7 cm and a height equal to 3.5 cm. Notice that we can only find the height by dropping a perpendicular to the base. The area is then

$A = \frac{1}{2} (7) (3.5) = 12.25 {cm}^{2} .$

A triangle with its base marked b equals 7 centimeters and height marked h equals 3.5 centimeters. — Figure 10.134: Triangle 2

Example 10.41: Finding the Area of a Triangle

Find the area of this triangle that has a base of 4 cm and the height is 6 cm (Figure 10.135).

A triangle with its base marked b equals 4 centimeters and height marked h equals 6 centimeters. — Figure 10.135

Answer

Using the formula, we have

$A = \frac{1}{2} (4) (6) = \frac{24}{2} = 12 {cm}^{2} .$

Your Turn 10.41

Find the area of the triangle with a base equal to 4 cm and the height equal to 4 cm.

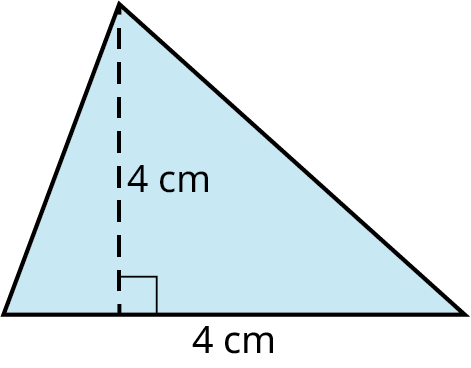
A triangle with its base marked 4 centimeters and height marked 4 centimeters. — Figure 10.136

Area of Quadrilaterals

A quadrilateral is a four-sided polygon with four vertices. Some quadrilaterals have either one or two sets of parallel sides. The set of quadrilaterals include the square, the rectangle, the parallelogram, the trapezoid, and the rhombus. The most common quadrilaterals are the square and the rectangle.

Square

In Figure 10.106, a 12 in $\times 12$ in grid is represented with twelve 1 in $\times 1$ in squares across each row, and twelve 1 in $\times 1$ in squares down each column. If you count the little squares, the sum equals 144 squares. Of course, you do not have to count little squares to find area-we have a formula. Thus, the formula for the area of a square, where $s=$ length of a side, is $A=s \cdot s$. The area of the square in Figure 10.106 is $A=12$ in $\times 12$ in = $144 \mathrm{in}^2$.

FORMULA

The formula for the area of a square is $A = s \cdot s$ or $A = s^{2} .$

Rectangle

Similarly, the area for a rectangle is found by multiplying length times width. The rectangle in Figure 10.138 has width equal to 5 in and length equal to 12 in. The area is $A = 5 (12) = 60 {in}^{2} .$

FORMULA

The area of a rectangle is given as $A = l w .$

Many everyday applications require the use of the perimeter and area formulas. Suppose you are remodeling your home and you want to replace all the flooring. You need to know how to calculate the area of the floor to purchase the correct amount of tile, or hardwood, or carpet. If you want to paint the rooms, you need to calculate the area of the walls and the ceiling to know how much paint to buy, and the list goes on. Can you think of other situations where you might need to calculate area?

Example 10.42: Finding the Area of a Rectangle

You have a garden with an area of 196 square feet. How wide can the garden be if the length is 28 feet?

Answer

The area of a rectangular region is $A = l w .$ Letting the width equal $w$ :

$\begin{matrix} 196 & = & 28 w \\ \frac{196}{28} & = & w = 7 ft \end{matrix}$

Your Turn 10.42

Find the area of a rectangular region with a length of 18 feet and a width 1/3 of the length.

Example 10.43: Determining the Cost of Floor Tile

Jennifer is planning to install vinyl floor tile in her rectangular-shaped basement, which measures 29 ft by 16 ft. How many boxes of floor tile should she buy and how much will it cost if one box costs $50 and covers $20 {ft}^{2} ?$

Answer: The area of the basement floor is $A = 29 (16) = 464 {ft}^{2} .$ We will divide this area by $20 ft .$ Thus, $\frac{464}{20} = 23.2 .$ Therefore, Jennifer will have to buy 24 boxes of tile at a cost $1,200.

Your Turn 10.43

You remodel your kitchen and decide to change out the tile floor. The floor measures 30 ft by 15 ft. One box of tile costs $45 and covers 10 ft². How many boxes of tile should you buy, and what will it cost?

Parallelogram

The area of a parallelogram can be found using the formula for the area of a triangle. Notice in Figure 10.139, if we cut a diagonal across the parallelogram from one vertex to the opposite vertex, we have two triangles. If we multiply the area of a triangle by 2, we have the area of a parallelogram:

$\begin{matrix} A & = & 2 (\frac{1}{2} b h) \\ A & = \end{matrix} \begin{matrix} b h \end{matrix}$

A parallelogram with its base marked b and height marked h. — Figure 10.139: Area of a Parallelogram

FORMULA

The area of a parallelogram is $A = b h .$

For example, if we have a parallelogram with the base be equal to 10 inches and the height equal to 5 inches, the area will be $A = (10) (5) = 50 {in}^{2} .$

Example 10.44: Finding the Area of a Parallelogram

In the parallelogram (Figure 10.140), if $F B = 10, A D = 15,$ find the exact area of the parallelogram.

A parallelogram, A B C D. A vertical dashed line is drawn from B to meet the side, A D at F. B F measures 10 centimeters, and F D measures 15 centimeters. — Figure 10.140

Answer

Using the formula of $A = b h,$ we have

$A = 10 (15) = 150 {cm}^{2} .$

Your Turn 10.44

Find the area of the parallelogram.

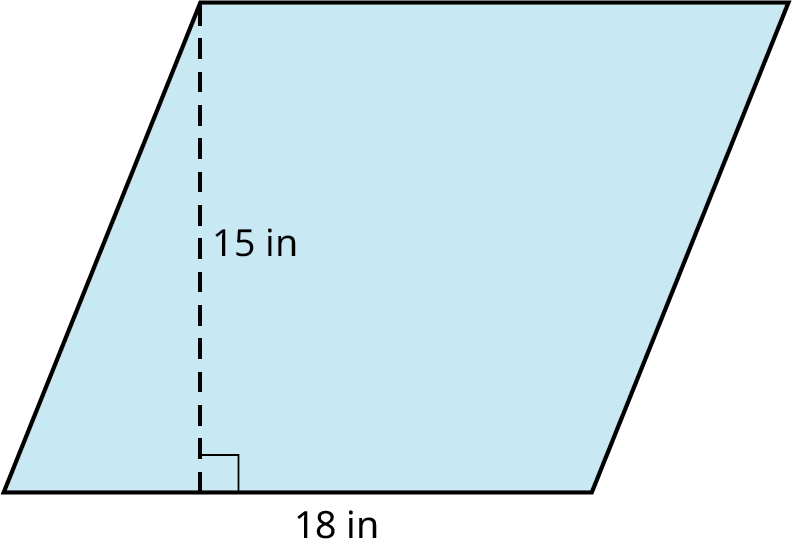
A parallelogram with its base marked 18 inches and height marked 15 inches. — Figure 10.141

Example 10.45: Finding the Area of a Parallelogram Park

The boundaries of a city park form a parallelogram (Figure 10.142). The park takes up one city block, which is contained by two sets of parallel streets. Each street measures 55 yd long. The perpendicular distance between streets is 39 yd. How much sod, sold by the square foot, should the city purchase to cover the entire park and how much will it cost? The sod is sold for $0.50 per square foot, installation is $1.50 per square foot, and the cost of the equipment for the day is $100.

A park is in the shape of a parallelogram. The sides measure 55 yards. The height measures 39 yards. — Figure 10.142

Answer

Step 1: As sod is sold by the square foot, the first thing we have to do is translate the measurements of the park from yards to feet. There are 3 ft to a yard, so 55 yd is equal to 165 ft, and 39 yd is equal to 117 ft.

Step 2: The park has the shape of a parallelogram, and the formula for the area is $A = b h$ :

$A = 165 (117) = 19,305 {ft}^{2} .$

Step 3: The city needs to purchase $19, 305 {ft}^{2}$ of sod. The cost will be $0.50 per square foot for the sod and $1.50 per square foot for installation, plus $100 for equipment:

$\begin{matrix} 19,305 ($ 0.50) + 19,305 ($ 1.50) & = & $ 9,652.5 + $ 28,957.5 + $ 100.00 \\ = & $ 38,710.00 \end{matrix}$

Your Turn 10.45

Suppose your city has a park just like the one in Example 10.45. The length of each street is 49 yd, and the perpendicular distance between streets is 31 yd. How much sod, sold by the square foot at $0.45 per square foot plus $1.00 per square foot for installation, and a flat $50 fee for equipment, should be purchased and what will the cost be?

Trapezoid

Another quadrilateral is the trapezoid. A trapezoid has one set of parallel sides or bases. The formula for the area of a trapezoid with parallel bases $a$ and $b$ and height $h$ is given here.

FORMULA

The formula for the area of a trapezoid is given as $A = \frac{1}{2} h (a + b) .$

For example, find the area of the trapezoid in Figure 10.143 that has base $a$ equal to 8 cm, base $b$ equal to 6 cm, and height equal to 6 cm.

A trapezoid with the bottom and top bases marked a and b. The height is marked h. — Figure 10.143: Area of a Trapezoid

\[\text { The area is } A=\frac{1}{2}(6)(6+8)=42 \mathrm{~cm}^2 \text {. }\]

Example 10.46: Finding the Area of a Trapezoid

$A B C D$ (Figure 10.112) is a regular trapezoid with $\overline{A B} \| \overline{C D}$. Find the exact perimeter of $A B C D$, and then find the area.

A trapezoid, A B C D. A B measures 11 inches. A D measures 13.5 inches. D C measures 31 inches. Two dashed vertical lines are drawn from A and B to meet the side, D C. The dashes lines are labeled h equals 10 inches. — Figure 10.144

Answer: The perimeter is the measure of the boundary of the shape, so we just add up the lengths of the sides. We have $P = 31 + 13.5 + 11 + 13.5 = 69 in .$ Then, the area of the trapezoid using the formula is $A = \frac{1}{2} (10) (11 + 31) = 210 {in}^{2}$ .

Your Turn 10.46

Find the area of the trapezoid shown.

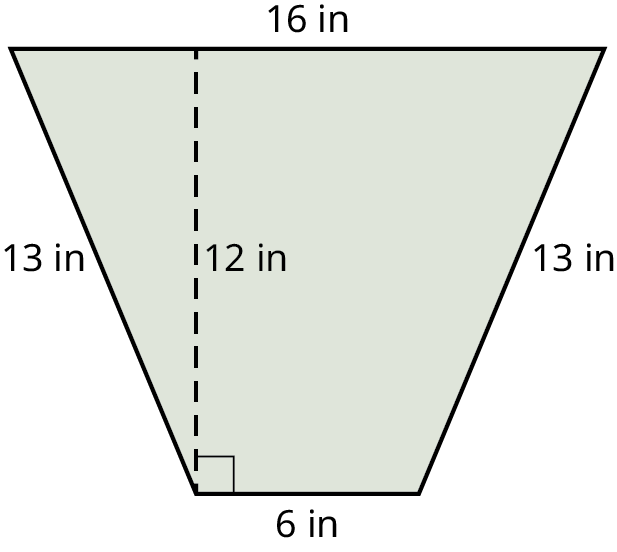
A trapezoid with its top and bottom sides marked 16 inches and 6 inches. The left and right sides are marked 13 inches. The height is marked 12 inches. — Figure 10.145

Rhombus

The rhombus has two sets of parallel sides. To find the area of a rhombus, there are two formulas we can use. One involves determining the measurement of the diagonals.

FORMULA

The area of a rhombus is found using one of these formulas:

$A=\dfrac{d_1 d_2}{2}$, where $d_1$ and $d_2$ are the diagonals.
$A=\dfrac{1}{2} b h$, where $b$ is the base and $h$ is the height.

For our purposes here, we will use the formula that uses diagonals. For example, if the area of a rhombus is $220 \mathrm{~cm}^2$, and the measure of $d_2=11$, find the measure of $d_1$. To solve this problem, we input the known values into the formula and solve for the unknown. See Figure 10.113.

A rhombus with two diagonal lines labeled d subscript 1 and d subscript 2. The line, d subscript 2 measures 11. — Figure 10.146: Area of a Rhombus

We have that

\[
\begin{aligned}
220 & =\dfrac{11 d_1}{2} \\
220(2) & =11 d_1 \\
\dfrac{440}{11} & =d_1=40
\end{aligned}
\] $\begin{matrix} \end{matrix}$

Example 10.47: Finding the Area of a Rhombus

Find the measurement of the diagonal $d_1$ if the area of the rhombus is $240 \mathrm{~cm}^2$, and the measure of $d_2=24 \mathrm{~cm}$

Answer

Use the formula with the known values:

\[
\begin{aligned}
240 & =\dfrac{d_1(24)}{2} \\
240(2) & =d_1(24) \\
\dfrac{480}{24} & =d_1=20
\end{aligned}
\]

$\begin{matrix} \end{matrix}$

Your Turn 10.47

A rhombus has an area of $40{\text{ in}^2}$, the measure of ${d_1} = 8$. Find the measure of ${d_2}$.

Example 10.48: Finding the Area of a Rhombus

You notice a child flying a rhombus-shaped kite on the beach. When it falls to the ground, it falls on a beach towel measuring 36inFigure 10.147)?

A rhombus-shaped kite with two diagonal lines. The horizontal diagonal line is labeled d subscript 1 equals 36 inches. The vertical diagonal line is labeled d subscript 2 equals 38 inches. — Figure 10.147

Answer

Using the formula, we have:

\[
\begin{aligned}
A & =\frac{d_1 d_2}{2} \\
& =\frac{36(38)}{2}=684 \mathrm{in}^2
\end{aligned}
\] $\begin{matrix} \end{matrix}$

Your Turn 10.48

You have a kite that measures $500\,{\text{i}}{{\text{n}}^2}.$ If one of the diagonals measures 25 in, what is the length of the other diagonal?

Area of Polygons

To find the area of a regular polygon, we need to learn about a few more elements. First, the apothem $a$ of a regular polygon is a line segment that starts at the center and is perpendicular to a side. The radius $r$ of a regular polygon is also a line segment that starts at the center but extends to a vertex. See Figure 10.115.

A hexagon with its radius marked r and apothem marked a. — Figure 10.148: Apothem and Radius of a Polygon

FORMULA

The area of a regular polygon is found with the formula $A = \frac{1}{2} a p,$ where $a$ is the apothem and $p$ is the perimeter.

For example, consider the regular hexagon shown in Figure 10.149 with a side length of 4 cm, and the apothem measures $a = 2 \sqrt{3} .$

A hexagon with its center marked C. Each side measures 4 centimeters. The apothem is marked a equals 2 times square root of 3. — Figure 10.149: Area of a Hexagon

We have the perimeter, $p = 6 (4) = 24 cm .$ We have the apothem as $a = 2 \sqrt{3} .$ Then, the area is:

$\begin{matrix} A & = & \frac{1}{2} (2 \sqrt{3}) (24) \\ = & 24 \sqrt{3} = 41.57 {cm}^{2} \end{matrix}$

Example 10.49: Finding the Area of a Regular Octagon

Find the area of a regular octagon with the apothem equal to 18 cm and a side length equal to 13 cm (Figure 10.150).

An octagon. Each side measures 13 centimeters. The apothem is marked a equals 18 centimeters. — Figure 10.150

Answer: Using the formula, we have the perimeter $p = 8 (13) = 104 cm .$ Then, the area is $A = \frac{1}{2} (10) (104) = 936 {cm}^{2} .$

Your Turn 10.49

Find the area of the regular pentagon with the apothem equal to 5.5 cm and the side length equal to 7 cm.

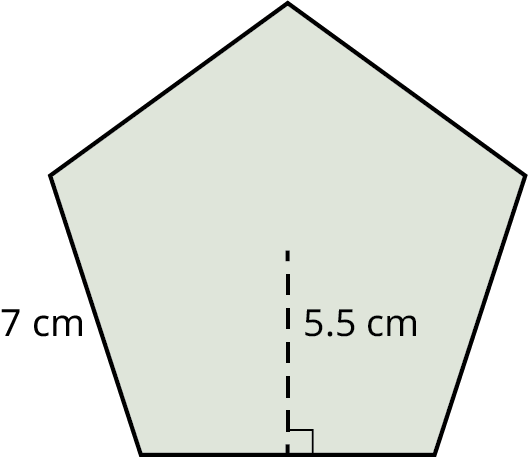
A pentagon. Each side measures 7 centimeters. The apothem is marked 5.5 centimeters. — Figure 10.151

Changing Units

Often, we have the need to change the units of one or more items in a problem to find a solution. For example, suppose you are purchasing new carpet for a room measured in feet, but carpeting is sold in terms of yards. You will have to convert feet to yards to purchase the correct amount of carpeting. Or, you may need to convert centimeters to inches, or feet to meters. In each case, it is essential to use the correct equivalency.

Example 10.50: Changing Units

Carpeting comes in units of square yards. Your living room measures 21 ft wide by 24 ft long. How much carpeting do you buy?

Answer: We must convert feet to yards. As there are 3 ft in 1 yd, we have $21 ft = 7 yds$ and $24 ft = 8 yds .$ Then, $7 (8) = 56 {yd}^{2} .$

Your Turn 10.50

You want to carpet your bedroom, which measures 15 ft wide by 18 ft long. Carpeting is sold by the square yard, so you must convert your measurements to yards. How much carpeting do you buy?

Area of Circles

Just as the circumference of a circle includes the number $π,$ so does the formula for the area of a circle. Recall that $π$ is a non-terminating, non-repeating decimal number: $π = 3.14159 \dots$ . It represents the ratio of the circumference to the diameter, so it is a critical number in the calculation of circumference and area.

FORMULA

The area of a circle is given as $A = π r^{2},$ where $r$ is the radius.

For example, to find the of the circle with radius equal to 3 cm, as shown in Figure 10.152, is found using the formula $A = π r^{2} .$

A circle with its radius, r marked 3 centimeters. — Figure 10.152: Circle with Radius 3

We have

$\begin{matrix} A & = & π r^{2} \\ = & π {(3)}^{2} \\ = & 9 π = 28.27 {cm}^{2} \end{matrix}$

Example 10.51: Finding the Area of a Circle

Find the area of a circle with diameter of 16 cm.

Answer

The formula for the area of a circle is given in terms of the radius, so we cut the diameter in half. Then, the area is

$A = π {(8)}^{2} = 201.1 {cm}^{2} .$

Your Turn 10.51

Find the area of the circle with a radius of 3 cm.

Example 10.52: Determining the Better Value for Pizza

You decide to order a pizza to share with your friend for dinner. The price for an 8-inch diameter pizza is $7.99. The price for 16-inch diameter pizza is $13.99. Which one do you think is the better value?

Answer: The area of the 8-inch diameter pizza is $A = π {(4)}^{2} = 50.3 {in}^{2} .$ The area of the 16-inch diameter pizza is $A = π {(8)}^{2} = 201.1 {in}^{2} .$ Next, we divide the cost of each pizza by its area in square inches. Thus, $\frac{13.99}{201.1} = $ 0.07$ per square inch and $\frac{7.99}{50.3} = $ 0.16$ per square inch. So clearly, the 16-inch pizza is the better value.

Your Turn 10.52

You can buy a 9-inch diameter pizza for $10.99, or a 15-inch diameter pizza for $14.99. Which pizza is the better value?

Example 10.53: Applying Area to the Real World

You want to purchase a tinted film, sold by the square foot, for the window in Figure 10.153. (This problem should look familiar as we saw it earlier when calculating circumference.) The bottom part of the window is a rectangle, and the top part is a semicircle. Find the area and calculate the amount of film to purchase.

A figure shows a semicircle placed on top of a rectangle. The length and width of the rectangle are 10 feet and 5 feet. The diameter of the semicircle is 5 feet. — Figure 10.153

Answer: First, the rectangular portion has $A = 5 (10) = 50 {ft}^{2}$ . For the top part, we have a semicircle with a diameter of 5 ft, so the radius is 2.5 ft. We want one half of the area of a circle with radius 2.5 ft, so the area of the top semicircle part is $A = \frac{1}{2} π {(2.5)}^{2} = 9.8 {ft}^{2} .$ Add the area of the rectangle to the area of the semicircle. Then, the total area to be covered with the window film is $A = 50 + 9.8 = 59.8 {ft}^{2} .$

Your Turn 10.53

You decide to install a new front door with a semicircle top as shown in the figure. How much area will the new door occupy?

A door resembles a semicircle placed on top of a rectangle. The length and width of the rectangle are 6.25 feet and 3.5 feet. The diameter of the semicircle is 3.5 feet. — Figure 10.154

Area within Area

Suppose you want to install a round hot tub on your backyard patio. How would you calculate the space needed for the hot tub? Or, let’s say that you want to purchase a new dining room table, but you are not sure if you have enough space for it. These are common issues people face every day. So, let’s take a look at how we solve these problems.

Example 10.54: Finding the Area within an Area

The patio in your backyard measures 20 ft by 10 ft (Figure 10.155). On one-half of the patio, you have a 4-foot diameter table with six chairs taking up an area of approximately 36 sq feet. On the other half of the patio, you want to install a hot tub measuring 6 ft in diameter. How much room will the table with six chairs and the hot tub take up? How much area is left over?

A patio is divided into two equal parts. The length and width of the patio measure 20 feet and 10 feet. The left part of the patio has a table with six chairs. The right part of the patio has a hot tub whose diameter is marked 6 feet. — Figure 10.155

Answer: The hot tub has a radius of 3 ft. That area is then $A = π {(3)}^{2} =$ 9π=28.27ft2.A=π(3)2=9π=28.27ft2. The total square feet taken up with the table and chairs and the hot tub is $36 + 28.27 = 64.27 {ft}^{2} .$ The area left over is equal to the total area of the patio, 200ft2200ft2 minus the area for the table and chairs and the hot tub. Thus, the area left over is $200 - 64.27 = 135.7 {ft}^{2} .$

Your Turn 10.54

Find the area of the shaded region in the given figure.

A square is circumscribed about a circle. The diameter of the circle is marked 10 centimeters. Each side of the square measures 10 centimeters. The region outside the circle is shaded. — Figure 10.156

Example 10.55: Finding the Cost of Fertilizing an Area

A sod farmer wants to fertilize a rectangular plot of land 150 ft by 240 ft. A bag of fertilizer covers $5,$ 000ft25,000ft2 and costs $200. How much will it cost to fertilize the entire plot of land?

Answer: The plot of land is $36, 000 {ft}^{2} .$ 000ft2. It will take 7.2 bags of fertilizer to cover the land area. Therefore, the farmer will have to purchase 8 bags of fertilizer at $200 a bag, which comes to $1,600.

Your Turn 10.55

You want to install sod on one-half of your parallelogram-shaped backyard as shown. The patio covers the other half. Sod costs $50 a bag and covers $25\,{\text{f}}{{\text{t}}^2}.$ How much will it cost to buy the sod?

A parallelogram with a diagonal running from the top-left vertex to the bottom-right vertex. The region above the diagonal is shaded. The length and height of the parallelogram measure 25 feet and h equals 12 feet. — Figure 10.157

People in Mathematics: Heron of Alexandria

A sketch depicts Heron of Alexandria. — Figure 10.158: Heron of Alexandria (credit: "Heron of Alexandria" from 1688 German translation of Hero's Pneumatics/Wikimedia Commons, Public Domain) Heron of Alexandria, born around 20 A.D., was an inventor, a scientist, and an engineer. He is credited with the invention of the Aeolipile, one of the first steam engines centuries before the industrial revolution. Heron was the father of the vending machine. He talked about the idea of inserting a coin into a machine for it to perform a specific action in his book, *Mechanics and Optics*. His contribution to the field of mathematics was enormous. *Metrica*, a series of three books, was devoted to methods of finding the area and volume of three-dimensional objects like pyramids, cylinders, cones, and prisms. He also discovered and developed the procedures for finding square roots and cubic roots. However, he is probably best known for Heron’s formula, which is used for finding the area of a triangle based on the lengths of its sides. Given a triangle

A triangle, A B C. A B measures c. A C measures b. C B measures a. — Figure 10.159

Heron's formula is $A=\sqrt{s(s-a)(s-b)(s-c)}$, where $s$ is the semi-perimeter calculated as $s=\frac{a+b+c}{2}$.

Check Your Understanding

1. Find the area of the triangle with base equal to 3 cm and height equal to 5 cm.

2. The area of the sail in the sailboat is $125\,{\text{f}}{{\text{t}}^2}.$ The shortest length is 10 ft. What is the height of the sail?

$A sailboat with the mainsail resembling a right triangle. The height of the mainsail is marked h.$

3. Find the area of this parallelogram.

$A parallelogram with its base marked 14 centimeters and height marked 12 centimeters.$

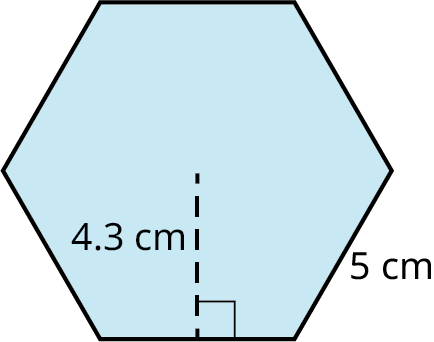
4. Find the area of a regular hexagon with side length of 5 and apothem equal to 4.3.

$A hexagon. Each side measures 5 centimeters. The apothem is marked 4.3 centimeters.$

5. Find the area of circle with a diameter of 16 in.

6. Find the area of the shaded region in the given figure.

$A circle is drawn with a trapezoid. The top and bottom bases of the trapezoid measure 18 inches and 22 inches. The radius of the circle is marked 4.5 inches. The circle touches the top and bottom bases of the trapezoid. The region outside the circle is shaded.$

7. A round tray sits on top of the dining room table. The radius of the tray is 15 in. What is the area taken up by the tray?