10.2: Angles

Figure $\PageIndex{1}$: This modern architectural design emphasizes sharp reflective angles as part of the aesthetic through the use of glass walls. (credit: “Société Générale @ La Défense @ Paris” by Images Guilhem Vellut/Flickr, CC BY 2.0)

Learning Objectives

1. Identify and express angles using proper notation.
2. Classify angles by their measurement.
3. Solve application problems involving angles.
4. Compute angles formed by transversals to parallel lines.
5. Solve application problems involving angles formed by parallel lines.

Unusual perspectives on architecture can reveal some extremely creative images. For example, aerial views of cities reveal some exciting and unexpected angles. Add reflections on glass or steel, lighting, and impressive textures, and the structure is a work of art. Understanding angles is critical to many fields, including engineering, architecture, landscaping, space planning, and so on. This is the topic of this section.

We begin our study of angles with a description of how angles are formed and how they are classified. An angle is the joining of two rays, which sweep out as the sides of the angle, with a common endpoint. The common endpoint is called the vertex. We will often need to refer to more than one vertex, so you will want to know the plural of vertex, which is vertices.

In Figure $\PageIndex{2}$ , let the ray $\overrightarrow{AB}$ stay put. Rotate the second ray $\overrightarrow{AC}$ in a counterclockwise direction to the size of the angle you want. The angle is formed by the amount of rotation of the second ray. When the ray $\overrightarrow{AC}$ continues to rotate in a counterclockwise direction back to its original position coinciding with ray $\overrightarrow{AB},$ the ray will have swept out ${360}^{\circ }.$ We call the rays the “sides” of the angle.

Figure $\PageIndex{2}$: Vertex and Sides of an Angle

Classifying Angles

Angles are measured in radians or degrees. For example, an angle that measures $\pi$ radians, or 3.14159 radians, is equal to the angle measuring $180^{\circ}$. An angle measuring $\frac{\pi}{2}$ radians, or 1.570796 radians, measures $90^{\circ}$. To translate degrees to radians, we multiply the angle measure in degrees by $\frac{\pi}{180}$. For example, to write $45^{\circ}$ in radians, we have

$$45^{\circ}\left(\frac{\pi}{180}\right)=\frac{\pi}{4}=0.785398 \text { radians. } \nonumber$$

To translate radians to degrees, we multiply by $\frac{180}{\pi}$. For example, to write $2 \pi$ radians in degrees, we have

$$2 \pi\left(\frac{180}{\pi}\right)=360^{\circ} \nonumber$$

Another example of translating radians to degrees and degrees to radians is $\frac{2 \pi}{3}$. To write in degrees, we have $\frac{2 \pi}{3}\left(\frac{180}{\pi}\right)=120^{\circ}$. To write $30^{\circ}$ in radians, we have $30^{\circ}\left(\frac{\pi}{180}\right)=\frac{\pi}{6}$. However, we will use degrees throughout this chapter.

FORMULA

To translate an angle measured in degrees to radians, multiply by $\frac{\pi}{180}$.

To translate an angle measured in radians to degrees, multiply by $\frac{180}{\pi}$. $$

Several angles are referred to so often that they have been given special names. A straight angle measures $180^{\circ}$; a right angle measures $90^{\circ}$; an acute angle is any angle whose measure is less than $90^{\circ}$; and an obtuse angle is any angle whose measure is between $90^{\circ}$ and $180^{\circ}$. See Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$: Classifying and Naming Angles

An easy way to measure angles is with a protractor (Figure $\PageIndex{4}$). A protractor is a very handy little tool, usually made of transparent plastic, like the one shown here.

Figure $\PageIndex{4}$: Protractor (credit: modification of work “School drawing tools” by Marco Verch/Flickr, CC BY 2.0)

With a protractor, you line up the straight bottom with the horizontal straight line of the angle. Be sure to have the center hole lined up with the vertex of the angle. Then, look for the mark on the protractor where the second ray lines up. As you can see from the image, the degrees are marked off. Where the second ray lines up is the measurement of the angle.

Checkpoint

Make sure you correctly match the center mark of the protractor with the vertex of the angle to be measured. Otherwise, you will not get the correct measurement. Also, keep the protractor in a vertical position.

Notation

Naming angles can be done in couple of ways. We can name the angle by three points, one point on each of the sides and the vertex point in the middle, or we can name it by the vertex point alone. Also, we can use the symbols $\angle$ or $\measuredangle$ before the points. When we are referring to the measure of the angle, we use the symbol $m \measuredangle$. See Figure $\PageIndex{5}$.

Figure $\PageIndex{5}$: Naming an Angle

We can name this angle $\measuredangle B A C$, or $\measuredangle C A B$, or $\measuredangle A$.$$

Example $\PageIndex{1}$: Classifying Angles

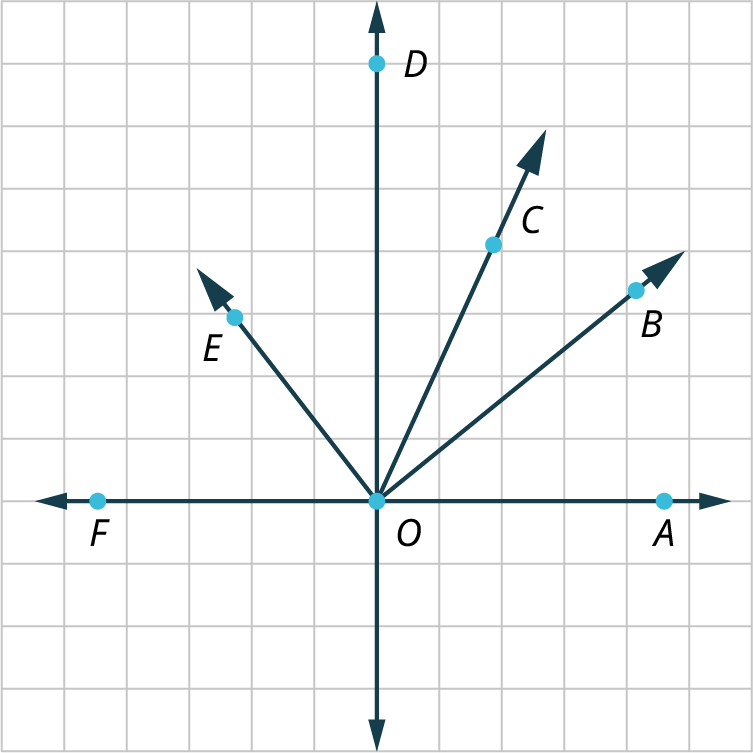
Determine which angles are acute, right, obtuse, or straight on the graph (Figure $\PageIndex{6}$). You may want to use a protractor for this one.

Figure $\PageIndex{}$

Answer

Acute angles measure less than ${90}^{\circ }.$	Obtuse angles measure between ${90}^{\circ }$ and ${180}^{\circ }.$	Right angles measure ${90}^{\circ }.$	Straight angles measure ${180}^{\circ }.$
∠EOF ∠EOG ∠FOG ∠GOH ∠FOH ∠HOJ ∠HOK ∠JOK ∠KOL ∠JOL	∠EOJ ∠EOK ∠FOJ ∠FOK ∠FOL ∠GOK ∠GOL	∠EOH ∠HOL ∠GOJ	$\angle$EOL

Most angles can be classified visually or by description. However, if you are unsure, use a protractor.

Your Turn $\PageIndex{1}$

Determine which angles are acute, obtuse, right, and straight in the graph.

Figure $\PageIndex{7}$

Adjacent Angles

Two angles with the same starting point or vertex and one common side are called adjacent angles. In Figure $\PageIndex{8}$, angle $\angle D B C$ is adjacent to $\angle C B A$. Notice that the way we designate an angle is with a point on each of its two sides and the vertex in the middle.

Figure $\PageIndex{8}$: Adjacent Angles

Supplementary Angles

TTwo angles are supplementary if the sum of their measures equals $180^{\circ}$. In Figure m∡ABE=145∘.

Figure $\PageIndex{9}$: Supplementary Angles

Example $\PageIndex{2}$: Solving for Angle Measurements and Supplementary Angles

Solve for the angle measurements in Figure $\PageIndex{10}$.

Figure $\PageIndex{10}$

Answer

Step 1: These are supplementary angles. We can see this because the two angles are part of a horizontal line, and a horizontal line represents $180^{\circ}$. Therefore, the sum of the two angles equals $180^{\circ}$.

Step 2:

$$\begin{aligned} (32 x-7)+(5 x+2) & =180 \\ 37 x-5 & =180 \\ 37 x & =185 \\ x & =5 \end{aligned} \nonumber$$

Step 3: Find the measure of each angle:

$$\begin{aligned} 32 x-7 & =32(5)-7 \\ & =153^{\circ} \\ 5 x+2 & =5(5)+2 \\ & =27^{\circ} \end{aligned} \nonumber$$

Step 4: We check: $153^{\circ}+27^{\circ}=180^{\circ}$.

$$

Your Turn $\PageIndex{2}$

Solve for the angle measurements in the figure shown.

Figure $\PageIndex{11}$

Complementary Angles

Two angles are complementary if the sum of their measures equals $90^{\circ}$. In Figure we have $m\measuredangle ABC={30}^{\circ },$ and $m\measuredangle ABD={90}^{\circ }.$ What is the $m\measuredangle CBD?$ These are complementary angles. Therefore, because ${90}^{\circ }-{30}^{\circ }={60}^{\circ },$ the $\measuredangle CBD={60}^{°}.$

Figure $\PageIndex{12}$: Complementary Angles

Example $\PageIndex{3}$: Solving for Angle Measurements and Complementary Angles

Solve for the angle measurements in Figure $\PageIndex{13}$

Figure $\PageIndex{13}$

Answer

We have that

$$\begin{aligned} (9 x-5)+4 x+(7 x-5) & =90 \\ 20 x & =100 \\ x & =5 \end{aligned} \nonumber$$

Then, $m \measuredangle(9 x-5)=40^{\circ}, m \measuredangle(4 x)=20^{\circ}$, and $m \measuredangle(7 x-5)=30^{\circ}$.$$

Your Turn $\PageIndex{3}$

Find the measure of each angle in the illustration.

Figure $\PageIndex{14}$

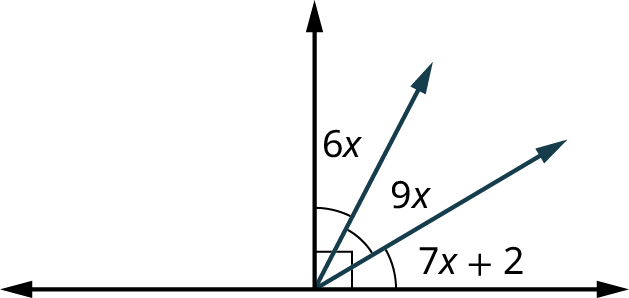
Vertical Angles

When two lines intersect, the opposite angles are called vertical angles, and vertical angles have equal measure. For example, Figure $\PageIndex{15}$ shows two straight lines intersecting each other. One set of opposite angles shows angle markers; those angles have the same measure. The other two opposite angles have the same measure as well.

Figure $\PageIndex{15}$: Vertical Angles

Example $\PageIndex{4}$: Calculating Vertical Angles

In Figure $\PageIndex{16}$, one angle measures ${40}^{\circ }.$ Find the measures of the remaining angles.

Figure $\PageIndex{16}$

Answer

The 40-degree angle and $\angle 2$ are vertical angles. Therefore, $m\measuredangle 2={40}^{\circ }.$

Notice that $\measuredangle 2$ and $\measuredangle 1$ are supplementary angles, meaning that the sum of $m\measuredangle 2$ and $m\measuredangle 1$ equals ${180}^{\circ }.$ Therefore, $m\measuredangle 1={180}^{\circ }-{40}^{\circ }={140}^{\circ }$.

Since $\measuredangle 1$ and $\measuredangle 3$ are vertical angles, then $m\measuredangle 3$ equals ${140}^{\circ }.$

Your Turn $\PageIndex{4}$

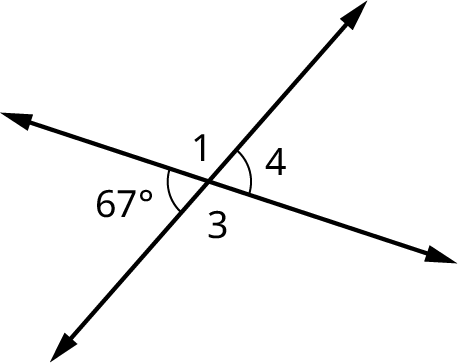
Given the two intersecting lines in the figure shown and $m\measuredangle 2 = {67^ \circ },$ find the measure of the remaining angles.

Figure $\PageIndex{17}$

Transversals

When two parallel lines are crossed by a straight line or transversal, eight angles are formed, including alternate interior angles, alternate exterior angles, corresponding angles, vertical angles, and supplementary angles. See Figure $\PageIndex{18}$. Angles 1, 2, 7, and 8 are called exterior angles, and angles 3, 4, 5, and 6 are called interior angles.

Figure $\PageIndex{18}$: Transversal

Alternate Interior Angles

Alternate interior angles are the interior angles on opposite sides of the transversal. These two angles have the same measure. For example, $\measuredangle 3$ and $\measuredangle 6$ are alternate interior angles and have equal measure; $\measuredangle 4$ and $\measuredangle 5$ are alternate interior angles and have equal measure as well. See Figure $\PageIndex{19}$.$$

Figure $\PageIndex{19}$: Alternate Interior Angles

Alternate Exterior Angles

Alternate exterior angles are exterior angles on opposite sides of the transversal and have the same measure. For example, in Figure $\PageIndex{20}$, $\measuredangle 2$ and $\measuredangle 7$ are alternate exterior angles and have equal measures; $\measuredangle 1$ and $\measuredangle 8$ are alternate exterior angles and have equal measures as well.

Figure $\PageIndex{20}$: Alternate Exterior Angles

Corresponding Angles

Corresponding angles refer to one exterior angle and one interior angle on the same side as the transversal, which have equal measures. In Figure $\PageIndex{21}$, $\measuredangle 1$ and $\measuredangle 5$ are corresponding angles and have equal measures; $\measuredangle 3$ and $\measuredangle 7$ are corresponding angles and have equal measures; $\measuredangle 2$ and $\measuredangle 6$ are corresponding angles and have equal measures; $\measuredangle 4$ and $\measuredangle 8$ are corresponding angles and have equal measures as well.

Figure $\PageIndex{21}$: Corresponding Angles

Example $\PageIndex{5}$: Evaluating Space

You live on the corner of First Avenue and Linton Street. You want to plant a garden in the far corner of your property (Figure $\PageIndex{22}$) and fence off the area. However, the corner of your property does not form the traditional right angle. You learned from the city that the streets cross at an angle equal to ${150}^{\circ }.$ What is the measure of the angle that will border your garden?

Figure $\PageIndex{22}$

Answer

As the angle between Linton Street and First Avenue is ${150}^{\circ },$ the supplementary angle is ${30}^{\circ }.$ Therefore, the garden will form a ${30}^{\circ }$ angle at the corner of your property.

Your Turn $\PageIndex{5}$

Suppose you have a similar property to the one in Figure $\PageIndex{22}$3, but the angle that corresponds to the garden corner is ${50^ \circ }$. What is the measure between the two cross streets?

Example $\PageIndex{6}$: Determining Angles Formed by a Transversal

In Figure $\PageIndex{23}$ given that angle 3 measures ${40}^{\circ },$ find the measures of the remaining angles and give a reason for your solution.

Figure $\PageIndex{23}$

Answer

$m\measuredangle 2=m\measuredangle 3={40}^{\circ }$ by vertical angles.

$\measuredangle 3=m\measuredangle 7$ by corresponding angles.

$m\measuredangle 7=m\measuredangle 6={40}^{\circ }$ by vertical angles.

$m\measuredangle 1=180-40={140}^{\circ }$ by supplementary angles.

$m\measuredangle 4=m\measuredangle 1={140}^{\circ }$ by vertical angles.

$m\measuredangle 8=m\measuredangle 1={140}^{\circ }$ by alternate exterior angles.

$m\measuredangle 5=m\measuredangle 8={140}^{\circ }$ by vertical angles.

Your Turn $\PageIndex{6}$

In the given figure if $m\measuredangle 1 = {120^ \circ }$, find the $m\measuredangle 5$, $m\measuredangle 4$, and $m\measuredangle 8$.

Figure $\PageIndex{24}$

Example $\PageIndex{7}$: Measuring Angles Formed by a Transversal

In Figure $\PageIndex{25}$ given that angle 2 measures ${23}^{\circ },$ find the measure of the remaining angles and state the reason for your solution.

Figure $\PageIndex{25}$

Answer

$m\measuredangle 2=m\measuredangle 3={23}^{\circ }$ by vertical angles, because $\measuredangle 2$ and $\measuredangle 3$ are the opposite angles formed by two intersecting lines.

$m\measuredangle 1={157}^{\circ }$ by supplementary angles to $m\measuredangle 2$ or $m\measuredangle 3.$ We see that $\measuredangle 1$ and $\measuredangle 2$ form a straight angle as does $\measuredangle 1$ and $\measuredangle 3.$ A straight angle measures ${180}^{\circ },$ so ${180}^{\circ }-{23}^{\circ }={157}^{\circ }.$

$m\measuredangle 4=m\measuredangle 1={157}^{\circ }$ by vertical angles, because $\measuredangle 4$ and $\measuredangle 1$ are the two opposite angles formed by two intersecting lines.

$m\measuredangle 5=m\measuredangle 1={157}^{\circ }$ by corresponding angles because they are the same angle formed by the transversal crossing two parallel lines, one exterior and one interior.

$m\measuredangle 8=m\measuredangle 5={157}^{\circ }$ by vertical angles because $\measuredangle 8$ and $\measuredangle 5$ are the two opposite angles formed by two intersecting lines.

$m\measuredangle 7=m\measuredangle 2={23}^{\circ }$ by alternate exterior angles because, like vertical angles, these angles are the opposite angles formed by the transversal intersecting two parallel lines.

$m\measuredangle 6=m\measuredangle 7={23}^{\circ }$ by vertical angles because these are the opposite angles formed by two intersecting lines.

Your Turn $\PageIndex{7}$

In the provided figure given that the $m\measuredangle 2 = {48^ \circ }$, find $m\measuredangle 1$, and $m\measuredangle 5.$

Figure $\PageIndex{26}$

Example $\PageIndex{8}$: Finding Missing Angles

Find the measures of the angles 1, 2, 4, 11, 12, and 14 in Figure $\PageIndex{27}$ and the reason for your answer given that $l_1$ and $l_2$ are parallel.

Figure $\PageIndex{27}$

Answer

$m\measuredangle 12={118}^{\circ }$, supplementary angles

$m\measuredangle 14={118}^{\circ }$, vertical angles

$m\measuredangle 11={62}^{\circ }$, vertical angles

$m\measuredangle 4={62}^{\circ }$, corresponding angles

$m\measuredangle 1={62}^{\circ }$, vertical angles

$m\measuredangle 2={56}^{\circ }$, supplementary angles

Your Turn $\PageIndex{8}$

Using Figure $\PageIndex{27}$, find the measures of angles 5, 6, 7, 8, and 9.

Who Knew?: The Number 360

Did you ever wonder why there are ${360}^{\circ }$ in a circle? Why not ${100}^{\circ }$ or ${500}^{\circ }?$ The number 360 was chosen by Babylonian astronomers before the ancient Greeks as the number to represent how many degrees in one complete rotation around a circle. It is said that they chose 360 for a couple of reasons: It is close to the number of days in a year, and 360 is divisible by 2, 3, 4, 5, 6, 8, 9, 10, …

Check Your Understanding

1.Classify the following angles as acute, right, obtuse, or straight.

• $m\measuredangle = {180^ \circ }$
• $m\measuredangle = {176^ \circ }$
• $m\measuredangle = {90^ \circ }$
• $m\measuredangle = {37^ \circ }$

2. For the following exercises, determine the measure of the angles in the given figure.

• Find the measure of $\measuredangle 1$ and state the reason for your solution.
• Find the measure of $\measuredangle 3$ and state the reason for your solution.
• Find the measure of $\measuredangle 5$ and state the reason for your solution.