10.6: Area
- Page ID
- 129645
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Calculate the area of triangles.
- Calculate the area of quadrilaterals.
- Calculate the area of other polygons.
- Calculate the area of circles.
Some areas carry more importance than other areas. Did you know that in a baseball game, when the player hits the ball and runs to first base that he must run within a 6-foot wide path? If he veers off slightly to the right, he is out. In other words, a few inches can be the difference in winning or losing a game. Another example is real estate. On Manhattan Island, one square foot of real estate is worth far more than real estate in practically any other area of the country. In other words, we place a value on area. As the context changes, so does the value.
Area refers to a region measured in square units, like a square mile or a square foot. For example, to purchase tile for a kitchen floor, you would need to know how many square feet are needed because tile is sold by the square foot. Carpeting is sold by the square yard. As opposed to linear measurements like perimeter, which in in linear units. For example, fencing is sold in linear units, a linear foot or yard. Linear dimensions refer to an outline or a boundary. Square units refer to the area within that boundary. Different items may have different units, but either way, you must know the linear dimensions to calculate the area.
Many geometric shapes have formulas for calculating areas, such as triangles, regular polygons, and circles. To calculate areas for many irregular curves or shapes, we need calculus. However, in this section, we will only look at geometric shapes that have known area formulas. The notation for area, as mentioned, is in square units and we write sq in or sq cm, or use an exponent, such as or Note that linear measurements have no exponent above the units or we can say that the exponent is 1.
Area of Triangles
The formula for the area of a triangle is given as follows.
The area of a triangle is given as where represents the base and represents the height.
For example, consider the triangle in Figure
The base measures 4 cm and the height measures 5 cm . Using the formula, we can calculate the area:
\[A=\frac{1}{2}(4)(5)=\frac{1}{2}(20)=10 \mathrm{~cm}^2 \nonumber \]
In Figure 10.104, the triangle has a base equal to 7 cm and a height equal to 3.5 cm . Notice that we can only find the height by dropping a perpendicular to the base. The area is then
\[A=\frac{1}{2}(7)(3.5)=12.25 \mathrm{~cm}^2 \nonumber \]
Find the area of this triangle that has a base of 4 cm and the height is 6 cm (Figure ).
- Answer
-
Using the formula, we have
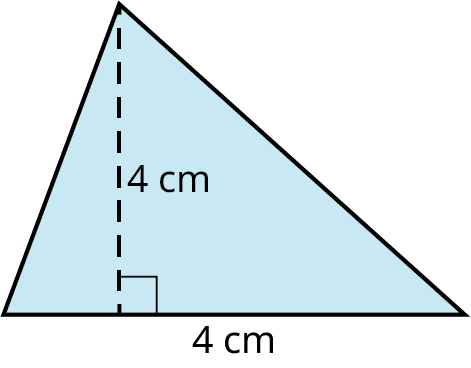
Find the area of the triangle with a base equal to 4 cm and the height equal to 4 cm.
Area of Quadrilaterals
A quadrilateral is a four-sided polygon with four vertices. Some quadrilaterals have either one or two sets of parallel sides. The set of quadrilaterals include the square, the rectangle, the parallelogram, the trapezoid, and the rhombus. The most common quadrilaterals are the square and the rectangle.
Square
In Figure , a 12 in \(\times 12\) in grid is represented with twelve 1 in \(\times 1\) in squares across each row, and twelve 1 in \(\times 1\) in squares down each column. If you count the little squares, the sum equals 144 squares. Of course, you do not have to count little squares to find area-we have a formula. Thus, the formula for the area of a square, where \(s=\) length of a side, is \(A=s \cdot s\). The area of the square in Figure is \(A=12\) in \(\times 12\) in = \(144 \mathrm{in}^2\).
The formula for the area of a square is \(A=s \cdot s\) or \(A=s^2\).
Rectangle
Similarly, the area for a rectangle is found by multiplying length times width. The rectangle in Figure 10.138 has width equal to 5 in and length equal to 12 in. The area is
The area of a rectangle is given as
Many everyday applications require the use of the perimeter and area formulas. Suppose you are remodeling your home and you want to replace all the flooring. You need to know how to calculate the area of the floor to purchase the correct amount of tile, or hardwood, or carpet. If you want to paint the rooms, you need to calculate the area of the walls and the ceiling to know how much paint to buy, and the list goes on. Can you think of other situations where you might need to calculate area?
You have a garden with an area of 196 square feet. How wide can the garden be if the length is 28 feet?
- Answer
-
The area of a rectangular region is \(A=l w\). Letting the width equal \(w\) :
\[\begin{aligned}
196 & =28 w \\
\frac{196}{28} & =w=7 \mathrm{ft}
\end{aligned} \nonumber \]
Find the area of a rectangular region with a length of 18 feet and a width 1/3 of the length.
Jennifer is planning to install vinyl floor tile in her rectangular-shaped basement, which measures 29 ft by 16 ft. How many boxes of floor tile should she buy and how much will it cost if one box costs $50 and covers
- Answer
-
The area of the basement floor is \(A=29(16)=464 \mathrm{ft}^2\). We will divide this area by 20 ft . Thus, \(\frac{464}{20}=23.2\). Therefore, Jennifer will have to buy 24 boxes of tile at a cost \(\$ 1,200\).
You remodel your kitchen and decide to change out the tile floor. The floor measures 30 ft by 15 ft. One box of tile costs $45 and covers 10 ft2. How many boxes of tile should you buy, and what will it cost?
Parallelogram
The area of a parallelogram can be found using the formula for the area of a triangle. Notice in Figure , if we cut a diagonal across the parallelogram from one vertex to the opposite vertex, we have two triangles. If we multiply the area of a triangle by 2 , we have the area of a parallelogram:
\[\begin{aligned}
A & =2\left(\frac{1}{2} b h\right) \\
A & =b h
\end{aligned} \nonumber \]
The area of a parallelogram is
For example, if we have a parallelogram with the base be equal to 10 inches and the height equal to 5 inches, the area will be
In the parallelogram (Figure ), if find the exact area of the parallelogram.
- Answer
-
Using the formula of we have
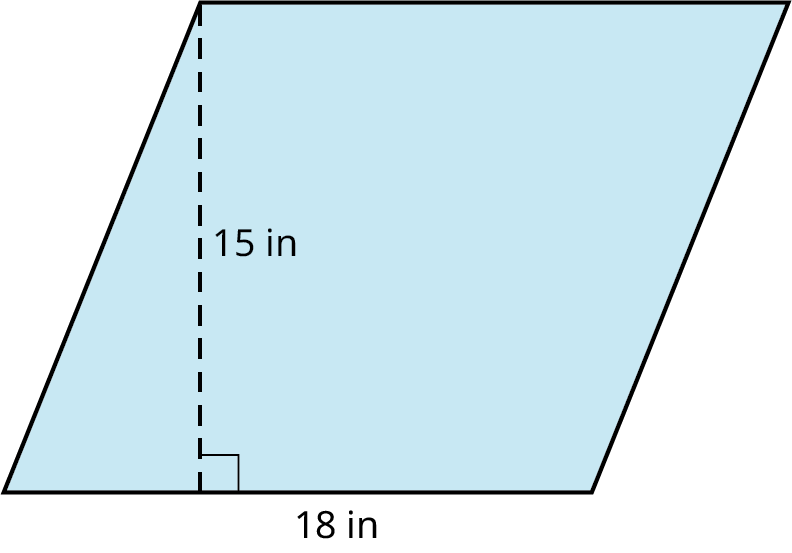
Find the area of the parallelogram.
The boundaries of a city park form a parallelogram (Figure ). The park takes up one city block, which is contained by two sets of parallel streets. Each street measures 55 yd long. The perpendicular distance between streets is 39 yd. How much sod, sold by the square foot, should the city purchase to cover the entire park and how much will it cost? The sod is sold for $0.50 per square foot, installation is $1.50 per square foot, and the cost of the equipment for the day is $100.
- Answer
-
Step 1: As sod is sold by the square foot, the first thing we have to do is translate the measurements of the park from yards to feet. There are 3 ft to a yard, so 55 yd is equal to 165 ft, and 39 yd is equal to 117 ft.
Step 2: The park has the shape of a parallelogram, and the formula for the area is \(A=b h\) :
\[A=165(117)=19,305 \mathrm{ft}^2 \nonumber \]
Step 3: The city needs to purchase \(19,305 \mathrm{ft}^2\) of sod. The cost will be \(\$ 0.50\) per square foot for the sod and \(\$ 1.50\) per square foot for installation, plus \(\$ 100\) for equipment:
\[\begin{aligned}
19,305(\$ 0.50)+19,305(\$ 1.50) & =\$ 9,652.5+\$ 28,957.5+\$ 100.00 \\
& =\$ 38,710.00
\end{aligned} \nonumber \]
Suppose your city has a park just like the one in Example . The length of each street is 49 yd, and the perpendicular distance between streets is 31 yd. How much sod, sold by the square foot at $0.45 per square foot plus $1.00 per square foot for installation, and a flat $50 fee for equipment, should be purchased and what will the cost be?
Trapezoid
Another quadrilateral is the trapezoid. A trapezoid has one set of parallel sides or bases. The formula for the area of a trapezoid with parallel bases and and height is given here.
The formula for the area of a trapezoid is given as
For example, find the area of the trapezoid in Figure that has base equal to 8 cm, base equal to 6 cm, and height equal to 6 cm.
The area is \(A=\frac{1}{2}(6)(6+8)=42 \mathrm{~cm}^2\).
\(A B C D\) (Figure ) is a regular trapezoid with \(\overline{A B} \| \overline{C D}\). Find the exact perimeter of \(A B C D\), and then find the area.
- Answer
-
The perimeter is the measure of the boundary of the shape, so we just add up the lengths of the sides. We have Then, the area of the trapezoid using the formula is .
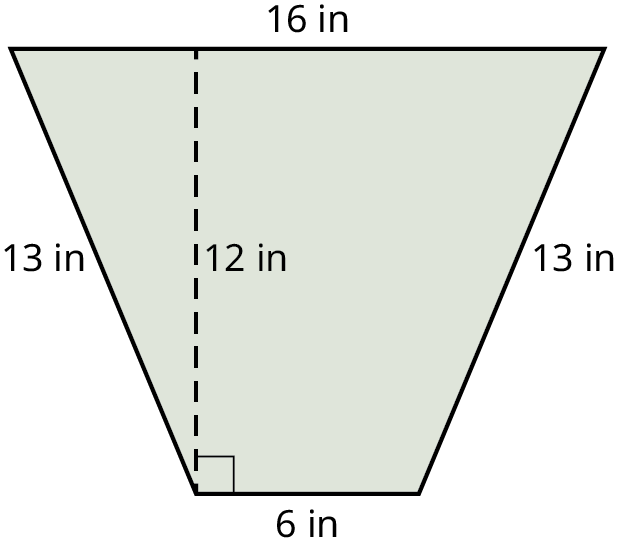
Find the area of the trapezoid shown.
Rhombus
The rhombus has two sets of parallel sides. To find the area of a rhombus, there are two formulas we can use. One involves determining the measurement of the diagonals.
The area of a rhombus is found using one of these formulas:
- \(A=\dfrac{d_1 d_2}{2}\), where \(d_1\) and \(d_2\) are the diagonals.
- \(A=\dfrac{1}{2} b h\), where \(b\) is the base and \(h\) is the height.
For our purposes here, we will use the formula that uses diagonals. For example, if the area of a rhombus is \(220 \mathrm{~cm}^2\), and the measure of \(d_2=11\), find the measure of \(d_1\). To solve this problem, we input the known values into the formula and solve for the unknown. See Figure .
We have that
\[\begin{aligned}
220 & =\dfrac{11 d_1}{2} \\
220(2) & =11 d_1 \\
\dfrac{440}{11} & =d_1=40
\end{aligned} \nonumber \]
Find the measurement of the diagonal \(d_1\) if the area of the rhombus is \(240 \mathrm{~cm}^2\), and the measure of \(d_2=24 \mathrm{~cm}\)
- Answer
-
Use the formula with the known values:
\[\begin{aligned}
240 & =\dfrac{d_1(24)}{2} \\
240(2) & =d_1(24) \\
\dfrac{480}{24} & =d_1=20
\end{aligned} \nonumber \]
A rhombus has an area of \(40{\text{ in}^2}\), the measure of \({d_1} = 8\). Find the measure of \({d_2}\).
You notice a child flying a rhombus-shaped kite on the beach. When it falls to the ground, it falls on a beach towel measuring
- Answer
-
Using the formula, we have:
\[\begin{aligned}
A & =\frac{d_1 d_2}{2} \\
& =\frac{36(38)}{2}=684 \mathrm{in}^2
\end{aligned} \nonumber \]
You have a kite that measures \(500\,{\text{i}}{{\text{n}}^2}.\) If one of the diagonals measures 25 in, what is the length of the other diagonal?
Area of Polygons
To find the area of a regular polygon, we need to learn about a few more elements. First, the apothem \(a\) of a regular polygon is a line segment that starts at the center and is perpendicular to a side. The radius \(r\) of a regular polygon is also a line segment that starts at the center but extends to a vertex. See Figure .
The area of a regular polygon is found with the formula where is the apothem and is the perimeter.
For example, consider the regular hexagon shown in Figure with a side length of 4 cm, and the apothem measures
We have the perimeter, \(p=6(4)=24 \mathrm{~cm}\). We have the apothem as \(a=2 \sqrt{3}\). Then, the area is:
\[\begin{aligned}
A & =\frac{1}{2}(2 \sqrt{3})(24) \\
& =24 \sqrt{3}=41.57 \mathrm{~cm}^2
\end{aligned} \nonumber \]
Find the area of a regular octagon with the apothem equal to 18 cm and a side length equal to 13 cm (Figure 0).
- Answer
-
Using the formula, we have the perimeter Then, the area is
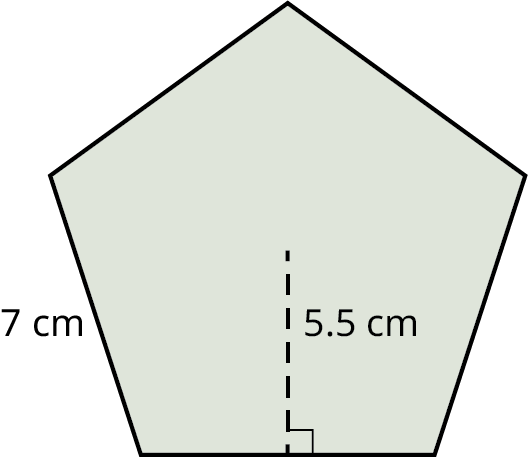
Find the area of the regular pentagon with the apothem equal to 5.5 cm and the side length equal to 7 cm.
Changing Units
Often, we have the need to change the units of one or more items in a problem to find a solution. For example, suppose you are purchasing new carpet for a room measured in feet, but carpeting is sold in terms of yards. You will have to convert feet to yards to purchase the correct amount of carpeting. Or, you may need to convert centimeters to inches, or feet to meters. In each case, it is essential to use the correct equivalency.
Carpeting comes in units of square yards. Your living room measures 21 ft wide by 24 ft long. How much carpeting do you buy?
- Answer
-
We must convert feet to yards. As there are 3 ft in 1 yd, we have and Then,
You want to carpet your bedroom, which measures 15 ft wide by 18 ft long. Carpeting is sold by the square yard, so you must convert your measurements to yards. How much carpeting do you buy?
Area of Circles
Just as the circumference of a circle includes the number so does the formula for the area of a circle. Recall that is a non-terminating, non-repeating decimal number: . It represents the ratio of the circumference to the diameter, so it is a critical number in the calculation of circumference and area.
The area of a circle is given as where is the radius.
For example, to find the of the circle with radius equal to 3 cm, as shown in Figure , is found using the formula
We have
\[\begin{aligned}
A & =\pi r^2 \\
& =\pi(3)^2 \\
& =9 \pi=28.27 \mathrm{~cm}^2
\end{aligned} \nonumber \]
Find the area of a circle with diameter of 16 cm.
- Answer
-
The formula for the area of a circle is given in terms of the radius, so we cut the diameter in half. Then, the area is
Find the area of the circle with a radius of 3 cm.
You decide to order a pizza to share with your friend for dinner. The price for an 8-inch diameter pizza is $7.99. The price for 16-inch diameter pizza is $13.99. Which one do you think is the better value?
- Answer
-
The area of the 8 -inch diameter pizza is \(A=\pi(4)^2=50.3 \mathrm{in}^2\). The area of the 16-inch diameter pizza is \(A=\pi(8)^2=201.1 \mathrm{in}^2\). Next, we divide the cost of each pizza by its area in square inches. Thus, \(\frac{13.99}{201.1}=\$ 0.07\) per square inch and \(\frac{7.99}{50.3}=\$ 0.16\) per square inch. So clearly, the 16 -inch pizza is the better value.
You can buy a 9-inch diameter pizza for $10.99, or a 15-inch diameter pizza for $14.99. Which pizza is the better value?
You want to purchase a tinted film, sold by the square foot, for the window in Figure . (This problem should look familiar as we saw it earlier when calculating circumference.) The bottom part of the window is a rectangle, and the top part is a semicircle. Find the area and calculate the amount of film to purchase.
- Answer
-
First, the rectangular portion has \(A=5(10)=50 \mathrm{ft}^2\). For the top part, we have a semicircle with a diameter of 5 ft , so the radius is 2.5 ft . We want one half of the area of a circle with radius 2.5 ft , so the area of the top semicircle part is \(A=\frac{1}{2} \pi(2.5)^2=9.8 \mathrm{ft}^2\). Add the area of the rectangle to the area of the semicircle. Then, the total area to be covered with the window film is
\[A=50+9.8=59.8 \mathrm{ft}^2\
You decide to install a new front door with a semicircle top as shown in the figure. How much area will the new door occupy?

Area within Area
Suppose you want to install a round hot tub on your backyard patio. How would you calculate the space needed for the hot tub? Or, let’s say that you want to purchase a new dining room table, but you are not sure if you have enough space for it. These are common issues people face every day. So, let’s take a look at how we solve these problems.
The patio in your backyard measures 20 ft by 10 ft (Figure ). On one-half of the patio, you have a 4-foot diameter table with six chairs taking up an area of approximately 36 sq feet. On the other half of the patio, you want to install a hot tub measuring 6 ft in diameter. How much room will the table with six chairs and the hot tub take up? How much area is left over?
- Answer
-
The hot tub has a radius of 3 ft . That area is then \(A=\pi(3)^2=9 \pi=28.27 \mathrm{ft}^2\). The total square feet taken up with the table and chairs and the hot tub is \(36+28.27=64.27 \mathrm{ft}^2\). The area left over is equal to the total area of the patio, \(200 \mathrm{ft}^2\) minus the area for the table and chairs and the hot tub. Thus, the area left over is \(200-64.27=135.7 \mathrm{ft}^2\).
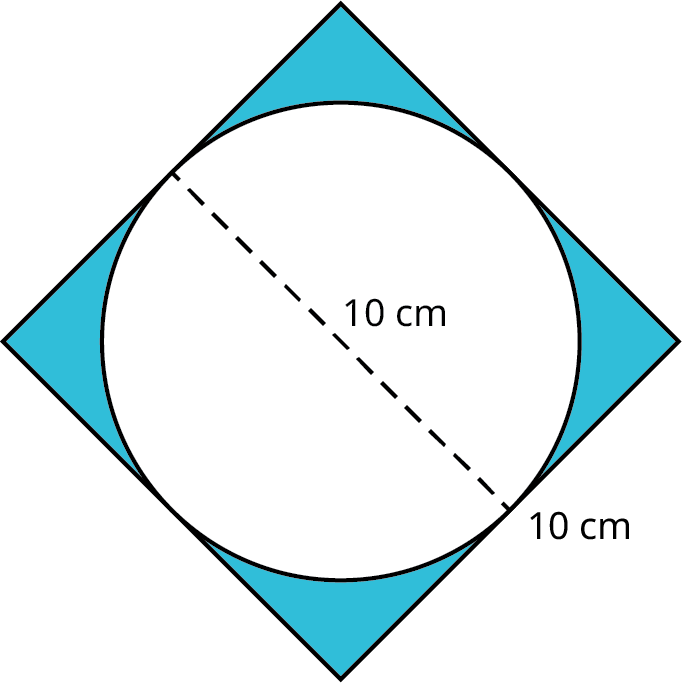
Find the area of the shaded region in the given figure.
A sod farmer wants to fertilize a rectangular plot of land 150 ft by 240 ft. A bag of fertilizer covers
- Answer
-
The plot of land is \(36,000 \mathrm{ft}^2\). It will take 7.2 bags of fertilizer to cover the land area. Therefore, the farmer will have to purchase 8 bags of fertilizer at \(\$ 200\) a bag, which comes to \$1,600.
You want to install sod on one-half of your parallelogram-shaped backyard as shown. The patio covers the other half. Sod costs \(\$ 50\) a bag and covers \(25 \mathrm{ft}^2\). How much will it cost to buy the sod?

Heron's formula is \(A=\sqrt{s(s-a)(s-b)(s-c)}\), where \(s\) is the semi-perimeter calculated as \(s=\frac{a+b+c}{2}\).
Check Your Understanding
1. Find the area of the triangle with base equal to 3 cm and height equal to 5 cm.
2. The area of the sail in the sailboat is \(125\,{\text{f}}{{\text{t}}^2}.\) The shortest length is 10 ft. What is the height of the sail?

3. Find the area of this parallelogram.

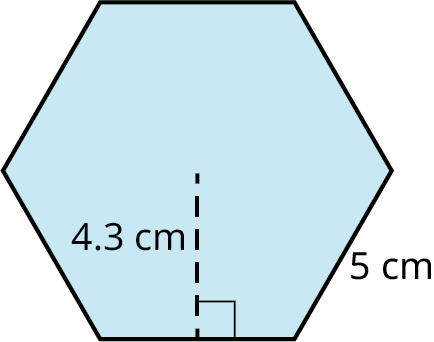
4. Find the area of a regular hexagon with side length of 5 and apothem equal to 4.3.
5. Find the area of circle with a diameter of 16 in.
6. Find the area of the shaded region in the given figure.

7. A round tray sits on top of the dining room table. The radius of the tray is 15 in. What is the area taken up by the tray?


