12.7: Hamilton Cycles

Last updated
Save as PDF

Page ID: 129675

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Describe and identify Hamilton cycles.
Compute the number of Hamilton cycles in a complete graph.
Apply and evaluate weighted graphs.

In Euler Circuits and Euler Trails, we looked for circuits and paths that visited each edge of a graph exactly once. In this section, we will look for circuits that visit each vertex exactly once. Like many concepts in graph theory, the idea of a circuit that visits each vertex once was inspired by games and puzzles. As early as the 9th century, Indian and Islamic intellectuals wondered whether it was possible for a knight to visit every space on a chess board of a given size, which is equivalent to visiting every vertex of a graph that represents the chess board.

A 3D model of an icosahedron. — Figure $\PageIndex{1}$: The symmetries of an icosahedron, with 30 edges, 20 faces, and 12 vertices, can be analyzed using graph theory. (credit: "Really big icosahedron" by Clayton Shonkwiler/Wikimedia, CC BY 2.0)

In 1857, a mathematician named William Rowan Hamilton invented a puzzle in which players were asked to find a route along the edges of a dodecahedron (see Figure 12.178), which visited every vertex exactly once. Let’s explore how graph theory provides insight into these games as well as practical applications such as the Traveling Salesperson Problem.

A dodecahedron. — Figure $\PageIndex{2}$ : A Dodecahedron

Hamilton’s Puzzle

Before we look at the solution to Hamilton's puzzle, let’s review some vocabulary we used in Figure $\PageIndex{3}$ . It will be helpful to remember that directed cycle is a type of circuit that doesn’t repeat any edges or vertices.

Three concentric ovals represent directed cycles, circuits, and closed walks. The first (inner) oval labeled directed cycles (closed paths) reads, no repeated edges or vertices. The second oval labeled circuits (closed talks) reads, no repeated edges. The third oval is labeled closed walks. — Figure $\PageIndex{3}$: Closed Walks, Circuits, and Directed Cycles

The goal of Hamilton's puzzle was to find a route along the edges of the dodecahedron, which visits each vertex exactly once. A dodecahedron is a three-dimensional space figure with faces that are all pentagons as we saw in Figure 12.178.

Since it is easier to visualize two dimensions rather than three, we will flatten out the dodecahedron and look at the edges and vertices on a flat surface. Graph A in Figure 12.180 shows a two-dimensional graph of the edges and vertices, and Graph B shows an untangled version of Graph A in which no edges are crossing. Graph B in Figure 12.180 is very similar to the design of the game board that Hamilton invented for his puzzle.

$Two graphs are labeled graph A and graph B. Graph A highlights the edges of a dodecahedron. Graph B highlights the vertices of a dodecahedron.$

$Two figures. The first figure is a 2 D view of a dodecahedron. The edges are highlighted. The second figure is a 3 D view of a dodecahedron. The edges in the front face are highlighted.$

Untangle graph

$Two graphs are labeled graph A and graph B. Graph A highlights the edges of a dodecahedron. Graph B highlights the vertices of a dodecahedron.$

Figure $\PageIndex{4}$: Graph of Edges and Vertices of Dodecahedron

We can see that this is a planar graph because it can be “untangled.” In order to solve Hamilton’s puzzle, we need to find a circuit that visits every vertex once. A solution is shown in Figure 12.181.

$A 2 D view of a dodecahedron. The edges are highlighted.$

$Two figures. The first figure is a 2 D view of a dodecahedron. The edges are highlighted. The second figure is a 3 D view of a dodecahedron. The edges in the front face are highlighted.$

In three Dimensions >

$Two figures. The first figure is a 2 D view of a dodecahedron. The edges are highlighted. The second figure is a 3 D view of a dodecahedron. The edges in the front face are highlighted.$

Figure $\PageIndex{5}$: A Solution to Hamilton’s Puzzle

A circuit that doesn’t repeat any vertices, like the one in Figure 12.181, is called a directed cycle. So, we can most accurately say that Hamilton’s puzzle asks us to find a directed cycle that visits every vertex in a graph exactly once. Because Hamilton created and solved this puzzle, these special circuits were named Hamilton cycles, or Hamilton circuits.

Who Knew?: Icosian Game

When Hamilton invented his puzzle in the 19th century, it was originally called the Icosian game. This was a reference to an icosahedron, not a dodecahedron. Why? Hamilton was actually interested in the symmetries of icosahedrons. It turns out that these two space figures are related to each other. The dodecahedron has 30 edges, 20 faces, and 12 vertices, while the icosahedron has 30 edges, 12 faces, and 20 vertices. By relating the vertices of the dodecahedron to the faces of the icosahedron, Hamilton was able to make the mathematical connections necessary to use graph theory and dodecahedrons to make discoveries about the symmetries of icosahedrons.

Hamilton Cycles vs. Euler Circuits

Let’s practice naming and identifying Hamilton cycles, as well as distinguishing them from Euler circuits. It is important to remember that Euler circuits visit all edges without repetition, while Hamilton cycles visit all vertices without repetition. Hamilton cycles are named by their vertices just like all circuits. An example is given in Figure $\PageIndex{6}$.

Two graphs. The first graph, graph Z has four vertices: a, b, c, and d. The edges connect a b, b c, c d, d a, and a c. The second graph directed edges from a to b, b to c, c to d, and d to a. A dashed line connects a to c. — Figure $\PageIndex{6}$: Hamilton Cycle in Graph Z

Notice that the Hamilton cycle a → b → c → d for Graph Z in Figure 12.182 is NOT an Euler circuit, because it does not visit edge acac. Some Hamilton cycles are also Euler circuits while some are not, and some Euler circuits are Hamilton cycles while some are not.

Checkpoint

TIP! Sometimes students confuse Euler circuits with Hamilton cycles. To help you remember, think of the E in Euler as standing for Edge.

Example $\PageIndex{1}$: Differentiating between Hamilton Cycles or Euler Circuits

Use Figure $\PageIndex{7}$ to determine whether the given circuit is a Hamilton cycle, an Euler circuit, both, or neither.

Graph Q has two overlapping quadrilaterals. The vertices of the outer quadrilateral are a, c, h, and f. The vertices of the inner quadrilateral are d, b, e, and g. The vertex, d rests on the edge a f. The vertex, b rests on the edge a c. The vertex, e rests on the edge c h. The vertex, g rests on the edge hf.

Figure 12.183 Graph Q

a → b → c → e → h → g → f → d → a
g → e → h → g → f → d → a → b → d → g
a → b → c → e → h → g → f → d → b → e → g → d → a

Answer

This circuit is a Hamilton cycle only. It visits each vertex exactly once, so, it is a Hamilton cycle. It is not an Euler circuit because it doesn’t visit all of the edges.
This circuit is neither Hamilton cycle nor an Euler circuit. It doesn’t visit vertex $c$ , so, it is not a Hamilton cycle. It also doesn’t visit edges bebe and cece, so, it is not an Euler circuit.
This circuit is an Euler circuit only. It visits several vertices more than once; so, it is not a Hamilton cycle. It visits every edge exactly once, so, it is an Euler circuit.

Checkpoint

TIP! Euler circuits never skip a vertex, so, they only fail to be Hamilton cycles when they visit a vertex more than once. Hamilton cycles never visit any edges twice, so, they only fail to be Euler circuits when they skip edges.

Your Turn $\PageIndex{1}$

Consider the figure shown. Is the circuit a → b → f → e → h → i → g → d → c → a an Euler circuit, a Hamilton cycle, or both?

Graph T has 9 vertices. The edges connect a b, b f, f e, e h, h i, I g, g d, d c, and c a. — Figure $\PageIndex{8}$: Graph T

Notice that the graph is a cycle. A cycle will always be Eulerian because all vertices are degree 2. Moreover, any circuit in the graph will always be both an Euler circuit and a Hamilton cycle. It is not always as easy to determine if a graph has a Hamilton cycle as it is to see that it has an Euler circuit, but there is a large group of graphs that we know will always have Hamilton cycles, the complete graphs. Since all vertices in a complete graph are adjacent, we can always find a directed cycle that visits all the vertices. For example, look at the directed six-cycle, n → o → p → q → r → s, in the complete graph with six vertices in Figure $\PageIndex{9}$.

A directed graph has six vertices: o, p, q, r, s, and n. All the vertices are interconnected. Directed arrows flow from o to p, p to q, q to r, r to s, s to n, and n to o. — Figure $\PageIndex{9}$: Directed Cycle in Complete Graph

That is not the only directed six-cycle in the graph though. We could find another just be reversing the direction, and we could find even more by using different edges. So, how many Hamilton cycles are in a complete graph with $n$ vertices? Before we tackle this problem, let’s look at a shorthand notation that we use in mathematics which will be helpful to us.

Factorials

In many areas of mathematics, we must calculate products like $7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$ or $11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$ , products that involve multiplying all the counting numbers from a particular number down to 1. Imagine that the product happened to be all the numbers from 100 down to 1. That’s a lot of writing! Instead of writing all of that out, mathematicians came up with a shorthand notation. For example, instead of $7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$ , we write $7!$ , which is read “7 factorial.” In other words, the product of all the counting numbers from $n$ down to 1 is called $n$ factorial and it is written $n!$

Example $\PageIndex{2}$: Evaluating Factorials

Evaluate $n!$ and $(n - 1)!$ for $n = 4$ .

Answer: $n! = 4! = 4 \cdot 3 \cdot 2 \cdot 1 =$ 24n!=4!=4⋅3⋅2⋅1=24 and $(n - 1)! = (4 - 1)! = 3! = 3 \cdot 2 \cdot 1 = 6$

Your Turn $\PageIndex{12}$

Evaluate $n!$ and $(n - 1)!$ for $n = 6$.

A common use for factorials is counting the number of ways to arrange objects. Suppose that there were three students, Aryana, Byron, and Carlos, who wanted to line up in a row. How many arrangements are possible? There are six possibilities: ABC, ACB, BAC, BCA, CAB, or CBA. Notice that there were three students being arranged, and the number of possible arrangements is three.

FORMULA

The number of ways to arrange $n$ distinct objects is $n!$ .

Example $\PageIndex{3}$: Counting Arrangements of Letters

Find the number of ways to arrange the letters a, b, c, and d.

Answer: $4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24$

Your Turn $\PageIndex{3}$

Find the number of ways to arrange the letters v, w, x, y, and z.

Counting Hamilton Cycles in Complete Graphs

Now, let’s get back to answering the question of how many Hamilton cycles are in a complete graph. In Table 12.8, we have drawn all the four cycles in a complete graph with four vertices. Remember, cycles can be named starting with any vertex in the cycle, but we will name them starting with vertex $a$ .

Table $\PageIndex{1}$ Four-Cycles in Complete Graph with Four Vertices
Complete Graph	Cycle	Cycle	Cycle
$A graph with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d.$	$A graph with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a c, and b d are in dashed lines.$	$A graph with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a d, and b c are in dashed lines.$	$A graph with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a b, and d c are in dashed lines.$
Cycle Name Clockwise	a, b, c, d	a, b, d, c	a, c, b, d
Cycle Name Counterclockwise	a, d, c, b	a, c, d, b	a, d, b, c

Table $\PageIndex{1}$ shows that there are three unique four-cycles in a complete graph with four vertices. Notice that there were two ways to name each cycle, one reading the vertices in a clockwise direction and one reading the vertices in a counterclockwise direction. This is important to us because we are interested in Hamilton cycles, which are directed cycles. Although the cycles (a, b, c, d) and (a, d, c, b) are the same cycle, the directed cycles, a → b → c → d → a and a → d → c → b → a, which travel the same route in reverse order are considered different directed cycles, as shown in Table $\PageIndex{2}$.

Table $\PageIndex{2}$ Hamilton Cycles in a Complete Graph with Four Vertices
Complete Graph	Cycle	Cycle	Cycle
$A grah with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d.$	$A grah with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a c, and b d are in dashed lines.$	$A grah with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a d, and b c are in dashed lines.$	$A grah with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a b, and d c are in dashed lines.$
Clockwise Hamilton Cycle	$A grah with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a c, and b d are in dashed lines. Directed edges flow from a to d, d to c, c to b, and b to a.$ a → b → c → d → a	$A grah with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a d, and b c are in dashed lines. The directed edges flow from a to c, c to d, d to b, and b to a.$ a → b → d → c → a	$A grah with four vertices, a, b, c, and d. Edges connect a b, b c, c d, d a, a c, and b d. The edges, a b, and d c are in dashed lines. The edges flow from a to d, d to b, b to c, c, and c to a.$ a → c → b → d → a
Counter-clockwise Hamilton Cycle	$In this graph, four vertices, a, b, c, and d are present. Edges connect a b, b c, c d, d a, a c, and b d. In this eighth graph, the edges, a c, and b d are in dashed lines. Directed edges flow from a to d, d to c, c to b, and b to a.$ a → d → c → b → a	$In this graph, four vertices, a, b, c, and d are present. Edges connect a b, b c, c d, d a, a c, and b d. In this ninth graph, the edges, a d, and b c are in dashed lines. The directed edges flow from a to c, c to d, d to b, and b to a.$ a → c → d → b → a	$In this graph, four vertices, a, b, c, and d are present. Edges connect a b, b c, c d, d a, a c, and b d. In this tenth graph, the edges, a b, and d c are in dashed lines. The edges flow from a to d, d to b, b to c, c, and c to a.$ a → d → b → c → a

The six directed four-cycles in Table $\PageIndex{2}$ are the only distinct Hamilton cycles in a complete graph with four vertices. Six is also the number of ways to arrange the three letters b, c, and d. (Do you see why?) The number of ways to arrange three letters is $3! = 3 \cdot 2 \cdot 1 = 6$ . Similarly, the number of Hamilton cycles in a graph with five vertices is the number of ways to arrange four letters, which is $4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24$ . In general, to find the number of Hamilton cycles in a graph, we take one less than the number of vertices and find its factorial.

FORMULA

The number of distinct Hamilton cycles in a complete graph with $n$ vertices is $(n - 1)!$

Example $\PageIndex{4}$: Counting Hamilton Cycles in a Complete Graph

How many Hamilton cycles are in the complete graph in Figure $\PageIndex{10}$?

Graph L has five vertices: m, n, o, p, and q. All vertices are interconnected. — Figure $\PageIndex{10}$ Complete Graph L

Answer: There are five vertices in the graph. Using $n = 5$ , we have $(n - 1)! = (5 - 1)! = 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24$ Hamilton cycles.

Your Turn $\PageIndex{4}$

How many Hamilton cycles are in the graph?

Graph R has six vertices: s, t, x, u, w, and v. All vertices are interconnected. — Figure $\PageIndex{11}$: Complete Graph R

Weighted Graphs

Suppose that an officer in the U.S. Air Force who is stationed at Vandenberg Air Force base must drive to visit three other California Air Force bases before returning to Vandenberg. The officer needs to visit each base once. The vertices in the graph in Figure $\PageIndex{12}$ represent the four U.S. Air Force bases, Vandenberg, Edwards, Los Angeles, and Beale. The edges are labeled to with the driving distance between each pair of cities.

A graph represents the four California air force bases. The graph has four vertices: E, B, V, and L. The edge, E B is labeld 410 miles. The edge, B V is labeled 396 miles. The edge, V L is labeled 159 miles. The edge, L E is labeled 106 miles. The edge, L B is labeled 439 miles. The edge, E V is labeled 207 miles. — Figure $\PageIndex{12}$: Graph of Four California Air Force Bases

The graph in Figure $\PageIndex{12}$ is called a weighted graph, because each edge has been assigned a value or weight. The weights can represent quantities such as time, distance, money, or any quantity associated with the adjacent vertices joined by the edges. The total weight of any walk, trail, or path is the sum of the weights of the edges it visits.

Notice that the officer’s trip can be represented as a Hamilton cycle, because each of the four vertices in the graph is visited exactly once.

Example $\PageIndex{5}$: Finding Hamilton Cycles of Lowest Weight

Use Figure $\PageIndex{12}$ and the given Hamilton cycles to answer the following questions.

V → L → E → B → V

V → L → B → E → V

V → E → L → B → V

V → B → E → L → V

Which of the Hamilton cycles (directed cycles) lie on the same cycle (undirected cycle) in the graph?
Find the total weight of each cycle.
Of the four, which of the Hamilton cycles describes the shortest trip for the officer? Describe the route.

Answer

V → L → E → B → V and V → B → E → L → V follow the same edges in reverse order.
Any Hamilton cycles that lie on the same cycle will have the same edges and the same total weight.
V → L → E → B → V and V → B → E → L → V each have total weight $159 + 106 + 410 + 396 = 1071$ .

V → L → B → E → V has a total weight $159 + 439 + 410 + 207 = 1215$ .

V → E → L → B → V has a total weight $396 + 439 + 106 + 207 = 1148$ .
Hamilton cycles V → L → E → B → V and V → B → E → L → V each have the lowest total weight. The officer would take the route from Vandenberg, to Los Angeles, to Edwards, to Beale, and back to Vandenberg, or reverse that route.

Your Turn $\PageIndex{5}$

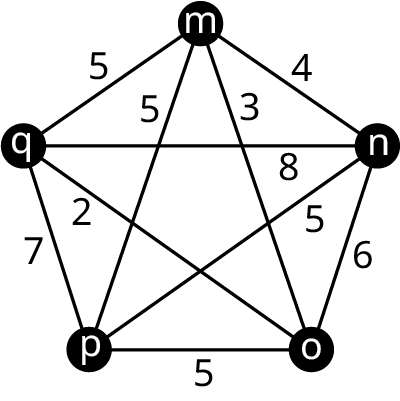
Find the weight of the Hamilton cycle m → o → p → n → q → m in the given figure.

A graph with 5 vertices: m, n, o, p, and q. The edges from m to q, p, o, and n are labeled 5, 5, 3, and 4. The edges from n to q, p, and o are labeled 8, 5, and 6. The edges from p to o and q are labeled 5 and 7. The edge from q to o is labeled 2. — Figure $\PageIndex{13}$: Weighted Complete Graph with Five Vertices

Check Your Understanding

For the following exercises, fill in the blank to make the statement true.

A Hamilton cycle is a circuit that visits each ___________ exactly once.
A __________ graph with $n \geq 3$ vertices has $\left( {n - 1} \right)!$ Hamilton cycles.
For the following exercises, fill in the blank with is or is not to make the statement true.
A Hamilton cycle ________ a circuit.
A Hamilton cycle that visits every edge ________ an Euler circuit.
A Hamilton cycle ________ different from a Hamilton circuit.
An Euler circuit that visits every vertex ________ a Hamilton cycle.
The total weight of a trail _______ the sum of the weights of the edges visited by the trail.
A weighted graph _______ always a complete graph.
The number of ways to arrange n objects _______ $\left( {n - 1} \right)!$
Every cycle ____ a circuit.

Search

Text Color

Text Size

Margin Size

Font Type

Who Knew?: Icosian Game

Checkpoint

Example \(\PageIndex{1}\): Differentiating between Hamilton Cycles or Euler Circuits

Checkpoint

Your Turn \(\PageIndex{1}\)

Example \(\PageIndex{2}\): Evaluating Factorials

Your Turn \(\PageIndex{12}\)

FORMULA

Example \(\PageIndex{3}\): Counting Arrangements of Letters

Your Turn \(\PageIndex{3}\)

FORMULA

Example \(\PageIndex{4}\): Counting Hamilton Cycles in a Complete Graph

Your Turn \(\PageIndex{4}\)

Example \(\PageIndex{5}\): Finding Hamilton Cycles of Lowest Weight

Your Turn \(\PageIndex{5}\)