1.6: Precision and GPE

Last updated
Save as PDF

Page ID: 56845

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Precision

The precision of a number is the place value of the rightmost significant figure. For example, $100.45$ is precise to the hundredths place, and $3,840$ is precise to the tens place.

Exercises $\PageIndex{1}$

Identify the precision (i.e., the place value of the rightmost significant figure) of each number.

1. $63,400$

2. $63,040$

3. $63,004$

4. $8,000$

5. $8,\overline{0}00$

6. $8,0\overline{0}0$

7. $8,00\overline{0}$

8. $0.085$

9. $0.0805$

10. $0.08050$

Answer

1. hundreds

2. tens

3. ones

4. thousands

5. hundreds

6. tens

7. ones

8. thousandths

9. ten thousandths

10. hundred thousandths

Precision-Based Rounding

In a previous module about decimals, we used precision-based rounding because we were rounding to a specified place value; for example, rounding to the nearest tenth. Let’s practice this with overbars and trailing zeros.

Precision-based rounding:

Locate the rounding digit in the place to which you are rounding.
Look at the test digit directly to the right of the rounding digit.
If the test digit is 5 or greater, increase the rounding digit by 1 and drop all digits to its right. If the test digit is less than 5, keep the rounding digit the same and drop all digits to its right.

Remember, when the rounding digit of a whole number is a $9$ that gets rounded up to a $0$, we must write an overbar above that $0$.

Also, when the rounding digit of a decimal number is a $9$ that gets rounded up to a $0$, we must include the $0$ in that decimal place.

Exercises $\PageIndex{1}$

Round each number to the indicated place value. Be sure to include trailing zeros or an overbar if necessary.

11. $13,997$ (thousands)

12. $13,997$ (hundreds)

13. $13,997$ (tens)

14. $0.5996$ (tenths)

15. $0.5996$ (hundredths)

16. $0.5996$ (thousandths)

Answer

11. $14,000$

12. $14,\overline{0}00$

13. $14,0\overline{0}0$

14. $0.6$

15. $0.60$

16. $0.600$

Precision when Adding and Subtracting

Suppose the attendance at a large event is estimated at $25,000$ people, but then you see $3$ people leave. Is the new estimate $24,997$? No, because the original estimate was precise only to the nearest thousand. We can’t start with an imprecise number and finish with a more precise number. If we estimated that $1,000$ people had left, then we could revise our attendance estimate to $24,000$ because this estimate maintains the same level of precision as our original estimate.

When adding or subtracting numbers with different levels of precision, the answer must be rounded to the same precision as the least precise of the original numbers.

Don’t round off the original numbers; do the necessary calculations first, then round the answer as your last step.

Exercises $\PageIndex{1}$

Add or subtract as indicated. Round to the appropriate level of precision.

17. Find the combined weight of four packages with the following weights: $9.7$ lb, $13$ lb, $10.5$ lb, $6.1$ lb.

18. Find the combined weight of four packages with the following weights: $9.7$ lb, $13.0$ lb, $10.5$ lb, $6.1$ lb.

19. While purchasing renter’s insurance, Chandra estimates the value of her insurable possessions at $ $10,200$. After selling some items valued at $ $375$, what would be the revised estimate?

20. Chandra knows that she has roughly $ $840$ in her checking account. After using her debit card to make two purchases of $ $25.95$ and $ $16.38$, how much would she have left in her account?

Answer

17. $39$ lb

18. $39.3$ lb

19. $ $9,800$

20. $ $8\overline{0}0$

If you are multiplying by an exact number, you can consider this a repeated addition. For example, suppose you measure the weight of an object to be $4.37$ ounces and you want to know the weight of three of these objects; multiplying $4.37$ times $3$ is the same as adding $4.37 + 4.37 + 4.37 = 13.11$ ounces. The precision is still to the hundredths place. The issue of significant figures doesn’t apply to exact numbers, so it would be wrong to treat $3$ as having only one sig fig. (Treat exact numbers like royalty; their precision is perfect and it would be an insult to even question it.)

$Crown-3.png$

Greatest Possible Measurement Error (GPE)

Suppose you are weighing a dog with a scale that displays the weight rounded to the nearest pound. If the scale says Sir Barks-A-Lot weighs $23$ pounds, he could weigh anywhere from $22.5$ pounds to almost $23.5$ pounds. The true weight could be as much as $0.5$ pounds above or below the measured weight, which we could write as $23\pm0.5$.

Now suppose you are weighing Sir Barks-A-Lot with a scale that displays the weight rounded to the nearest tenth of a pound. If the scale says Sir Barks-A-Lot weighs $23.0$ pounds, we now know that he could weigh anywhere from $22.95$ pounds to almost $23.05$ pounds. The true weight could be as much as $0.05$ pounds above or below the measured weight, which we could write as $23.0\pm0.05$.

As we increase the level of precision in our measurement, we decrease the greatest possible measurement error or GPE. The GPE is always one half the precision; if the precision is to the nearest tenth, $0.1$, the GPE is half of one tenth, or five hundredths, $0.05$. The GPE will always be a $5$ in the place to the right of the place value of the number’s precision.

Another way to think about the GPE is that it gives the range of values that would round off to the number in question. Back to weighing Sir Barks-A-Lot: $23\pm0.5$ tells us a lower value and an upper value. $23-0.5=22.5$ is the lowest weight that would round up to $23$. Similarly, $23+0.5=23.5$ is the highest weight that would round down to $23$. Yes, perhaps we should say $23.49$ or $23.499$, etc., for the upper limit here, but it is easier to just say $23.5$ and agree that $23.5$ is the upper limit even though it would round up instead of down. Using inequalities, we could represent $23\pm0.5$ as the range of values $22.5\leq\text{weight}<23.5$ instead.

$Belles-of-the-ball.jpg$

When you are asked to identify the GPE, it may help to think “What are the minimum and maximum numbers that would round to the given number?” For example, suppose the attendance at a Portland Thorns match is estimated to be $14,000$ people. This number is precise to the nearest thousand. The minimum number that would round up to $14,000$ would be $13,500$ (because $13,449$ would round down to $13,000$), and the maximum number that would round down to $14,000$ would be just below $14,500$ (because $14,500$ would round up to $15,000$). Because these numbers are each $500$ away from $14,000$, the GPE is $500$. If the estimate of $14,000$ is correct to the nearest thousand, we know that the actual attendance is within $\pm$500 of $14,000$.

Exercises $\PageIndex{1}$

21. A package weighs $3.76$ pounds. What is the GPE?

22. A roll of plastic sheeting is $0.00031$ inches thick. What is the GPE in inches?

23. Plastic sheeting $0.00031$ inches thick is referred to as $0.31$ mil. What is the GPE in mils?

Answer

21. $\pm 0.005$ lb

22. $\pm 0.000005$ in

23. $\pm 0.005$ mil

Recall from the previous module that the accuracy of a measurement is the number of significant figures. Let’s put together the ideas of accuracy, precision, and greatest possible measurement error.

Exercises $\PageIndex{1}$

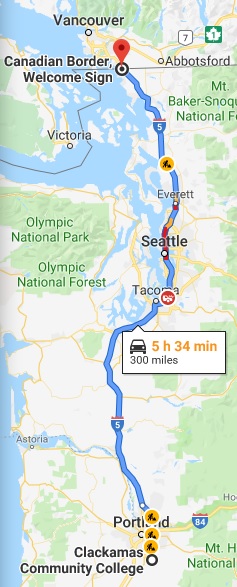
$Google Map showing a 300-mile route from Clackamas Community College north to the Canadian border$

Google Maps says that the driving distance from CCC’s main campus to the Canadian border is $300$ miles. (Note: this is rounded to the nearest mile.)

24. What is the accuracy?

25. What is the precision?

26. What is the GPE?

A new stadium is expected to have around $23,000$ seats.

27. What is the accuracy?

28. What is the precision?

29. What is the GPE?

The capacity of a car’s gas tank is $14.2$ gallons.

30. What is the accuracy?

31. What is the precision?

32. What is the GPE?

Answer

24. three significant figures

25. ones place; the nearest $1$ mile

26. $\pm 0.5$ mi

27. two significant figures

28. thousands place; the nearest $1,000$ seats

29. $\pm 500$ seats

30. three significant figures

31. tenths place; the nearest $0.1$ gallon

32. $\pm 0.05$ gal

Here is a summary of the important terms from these two modules. It is easy to get them mixed up, but remembering that “precision” and “place value” both start with “p” can be helpful.

Summary of Terms

Significant figures: the digits in a number that we trust to be correct

Accuracy: the number of significant digits

Precision: the place value of the rightmost significant digit

Greatest possible measurement error (GPE): one half the precision

Search

Exercises \(\PageIndex{1}\)

Exercises \(\PageIndex{1}\)

Exercises \(\PageIndex{1}\)

Exercises \(\PageIndex{1}\)

Exercises \(\PageIndex{1}\)