6.2: Surface Area of a Cube
- Page ID
- 39649
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lesson
Let's write a formula to find the surface area of a cube.
Exercise \(\PageIndex{1}\): Exponent Review
Select the greater expression of each pair without calculating the value of each expression. Be prepared to explain your choices.
- \(10\cdot 3\) or \(10^{3}\)
- \(13^{2}\) or \(12\cdot 12\)
- \(97+97+97+97+97+97\) or \(5\cdot 97\)
Exercise \(\PageIndex{2}\): The Net of a Cube
- A cube has edge length 5 inches.
- Draw a net for this cube, and label its sides with measurements.
- What is the shape of each face?
- What is the area of each face?
- What is the surface area of this cube?
- What is the volume of this cube?
- A second cube has edge length 17 units.
- Draw a net for this cube, and label its sides with measurements.
- Explain why the area of each face of this cube is \(17^{2}\) square units.
- Write an expression for the surface area, in square units.
- Write an expression for the volume, in cubic units.
Exercise \(\PageIndex{3}\): Every Cube in the Whole World
A cube has edge length \(s\).
- Draw a net for the cube.
- Write an expression for the area of each face. Label each face with its area.
- Write an expression for the surface area.
- Write an expression for the volume.
Summary
The volume of a cube with edge length \(s\) is \(s^{3}\).
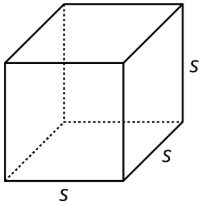
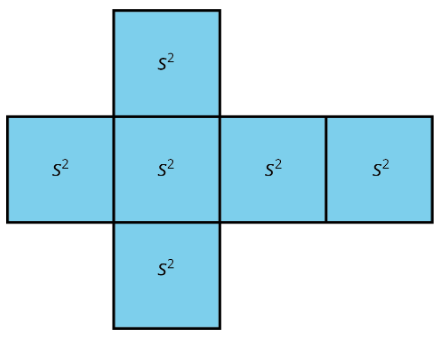
A cube has 6 faces that are all identical squares. The surface area of a cube with edge length \(s\) is \(6\cdot s^{2}\).
Glossary Entries
Definition: Cubed
We use the word cubed to mean “to the third power.” This is because a cube with side length \(s\) has a volume of \(s\cdot s\cdot s\), or \(s^{3}\).
Definition: Exponent
In expressions like \(5^{3}\) and \(8^{2}\), the 3 and the 2 are called exponents. They tell you how many factors to multiply. For example, \(5^{3} = 5\cdot 5\cdot 5\), and \(8^{2}=8\cdot 8\).
Definition: Squared
We use the word squared to mean “to the second power.” This is because a square with side length \(s\) has an area of \(s\cdot s\), or \(s^{2}\).
Practice
Exercise \(\PageIndex{4}\)
- What is the volume of a cube with edge length 8 in?
- What is the volume of a cube with edge length \(\frac{1}{3}\) cm?
- A cube has a volume of 8 ft3. What is its edge length?
Exercise \(\PageIndex{5}\)
- What three-dimensional figure can be assembled from this net?
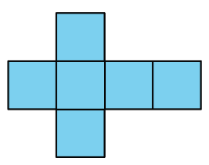
- If each square has a side length of 61 cm, write an expression for the surface area and another for the volume of the figure.
Exercise \(\PageIndex{6}\)
- Draw a net for a cube with edge length \(x\) cm.
- What is the surface area of this cube?
- What is the volume of this cube?
Exercise \(\PageIndex{7}\)
Here is a net for a rectangular prism that was not drawn accurately.
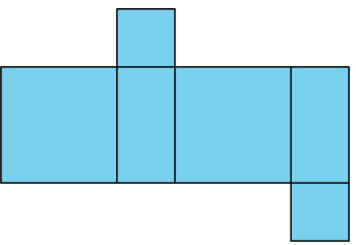
- Explain what is wrong with the net.
- Draw a net that can be assembled into a rectangular prism.
- Create another net for the same prism.
(From Unit 1.5.3)
Exercise \(\PageIndex{8}\)
State whether each figure is a polyhedron. Explain how you know.
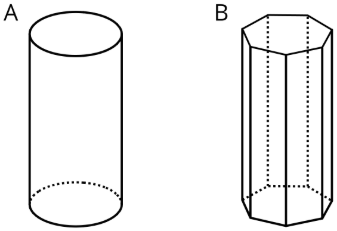
(From Unit 1.5.2)
Exercise \(\PageIndex{9}\)
Here is Elena’s work for finding the surface area of a rectangular prism that is 1 foot by 1 foot by 2 feet.
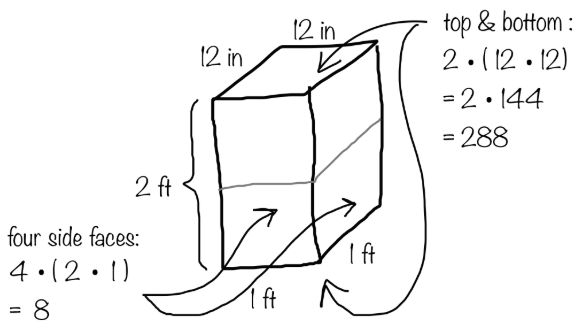
She concluded that the surface area of the prism is 296 square feet. Do you agree with her? Explain your reasoning.
(From Unit 1.5.1)


