21.2: Meanings of Division
- Page ID
- 40239
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lesson
Let's explore ways to think about division.
Exercise \(\PageIndex{1}\): A Division Expression
Here is an expression: \(20\div 4\).
What are some ways to think about this expression? Describe at least two meanings you think it could have.
Exercise \(\PageIndex{2}\): Bags of Almonds
A baker has 12 pounds of almonds. She puts them in bags, so that each bag has the same weight.
Clare and Tyler drew diagrams and wrote equations to show how they were thinking about \(12\div 6\).
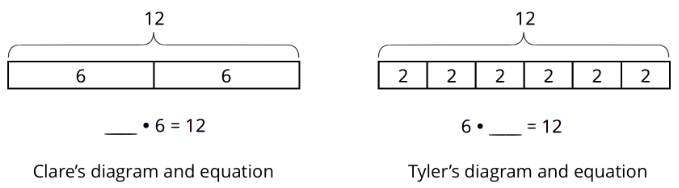
- How do you think Clare and Tyler thought about \(12\div 6\)? Explain what each diagram and the parts of each equation could mean about the situation with the bags of almonds. Make sure to include the meaning of the missing number.
Pause here for a class discussion. - Explain what each division expression could mean about the situation with the bags of almonds. Then draw a diagram and write a multiplication equation to show how you are thinking about the expression.
- \(12\div 4\)
- \(12\div 2\)
- \(12\div\frac{1}{2}\)
Are you ready for more?
A loaf of bread is cut into slices.
- If each slice is \(\frac{1}{2}\) of a loaf, how many slices are there?
- If each slice is \(\frac{1}{5}\) of a loaf, how many slices are there?
- What happens to the number of slices as each slice gets smaller?
- What would dividing by 0 mean in this situation about slicing bread?
Summary
Suppose 24 bagels are being distributed into boxes. The expression \(24\div 3\) could be understood in two ways:
- 24 bagels are distributed equally into 3 boxes, as represented by this diagram:

- 24 bagels are distributed into boxes, 3 bagels in each box, as represented by this diagram:

In both interpretations, the quotient is the same (\(24\div 3=8\)), but it has different meanings in each case. In the first case, the 8 represents the number of bagels in each of the 3 boxes. In the second, it represents the number of boxes that were formed with 3 bagels in each box.
These two ways of seeing division are related to how 3, 8, and 24 are related in a multiplication. Both \(3\cdot 8\) and \(8\cdot 3\) equal 24.
- \(3\cdot 8=24\) can be read as “3 groups of 8 make 24.”
- \(8\cdot 3=24\) can be read as “8 groups of 3 make 24.”
If 3 and 24 are the only numbers given, the multiplication equations would be: \(3\cdot ?=24\) \(?\cdot 3=24\)
In both cases, the division \(24\div 3\) can be used to find the value of the “?” But now we see that it can be interpreted in more than one way, because the “?” can refer to the size of a group (as in “3 groups of what number make 24?”), or to the number of groups (as in “How many groups of 3 make 24?”).
Practice
Exercise \(\PageIndex{3}\)
Twenty pounds of strawberries are being shared equally by a group of friends. The equation \(20\div 5=4\) represents the division of strawberries.
- If the 5 represents the number of people, what does the 4 represent?
- If the 5 represents the pounds of strawberries per person, what does the 4 represent?
Exercise \(\PageIndex{4}\)
A sixth-grade science club needs $180 to pay for the tickets to a science museum. All tickets cost the same amount.
What could \(180\div 15\) mean in this situation? Describe two different possible meanings of this expression. Then, find the quotient and explain what it means in each case.
Exercise \(\PageIndex{5}\)
Write a multiplication equation that corresponds to each division equation.
- \(10\div 5=?\)
- \(4.5\div 3=?\)
- \(\frac{1}{2}\div 4=?\)
Exercise \(\PageIndex{6}\)
Write a division or multiplication equation that represents each situation. Use a “?” for the unknown quantity.
- 2.5 gallons of water are poured into 5 equally sized bottles. How much water is in each bottle?
- A large bucket of 200 golf balls is divided into 4 smaller buckets. How many golf balls are in each small bucket?
- Sixteen socks are put into pairs. How many pairs are there?
Exercise \(\PageIndex{7}\)
Find a value for \(a\) that makes each statement true.
- \(a\div 6\) is greater than 1
- \(a\div 6\) is equal to 1
- \(a\div 6\) is less than 1
- \(a\div 6\) is equal to a whole number
(From Unit 4.1.1)
Exercise \(\PageIndex{8}\)
Complete the table. Write each percentage as a percent of 1.
| fraction | decimal | percentage |
|---|---|---|
| \(\frac{1}{4}\) | \(0.25\) | \(25\)% of \(1\) |
| \(0.1\) | ||
| \(75\)% of \(1\) | ||
| \(\frac{1}{5}\) | ||
| \(1.5\) | ||
| \(140\)% of \(1\) |
(From Unit 3.4.5)
Exercise \(\PageIndex{9}\)
Jada walks at a speed of 3 miles per hour. Elena walks at a speed of 2.8 miles per hour. If they both begin walking along a walking trail at the same time, how much farther will Jada walk after 3 hours? Explain your reasoning.
(From Unit 3.3.4)

