23.2: Using an Algorithm to Divide Fractions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Lesson
Let's divide fractions using the rule we learned.
Exercise 23.2.1: Multiplying Fractions
Evaulate each expression.
- 23⋅27
- 12⋅23
- 29⋅35
- 27100⋅2009
- (134)⋅57
Exercise 23.2.2: Dividing a Fraction by a Fraction
Work with a partner. One person works on the questions labeled “Partner A” and the other person works on those labeled “Partner B.”
- Partner A:
Find the value of each expression by completing the diagram.
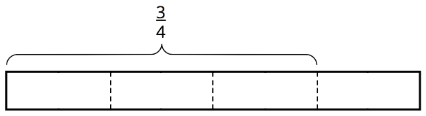
- 34÷18
How many 18s in 34?
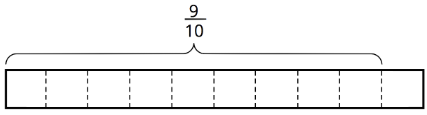
- 910÷35
How many 35s in 910?
Use the applet to confirm your answers and explore your own examples.
Partner B:
Elena said: “If I want to divide 4 by 25, I can multiply 4 by 5 and then divide it by 2 or multiply it by 12.”
Find the value of each expression using the strategy Elena described.
- 34÷18
- 910÷35
- What do you notice about the diagrams and expressions? Discuss with your partner.
- Complete this sentence based on what you noticed:
To divide a number n by a fraction ab, we can multiply n by ________ and then divide the product by ________. - Select all equations that represent the statement you completed.
- n÷ab=n⋅b÷a
- n÷ab=n⋅a÷b
- n÷ab=n⋅ab
- n÷ab=n⋅ba
Exercise 23.2.3: Using an Algorithm to Divide Fractions
Calculate each quotient. Show your thinking and be prepared to explain your reasoning.
- 89÷4
- 34÷12
- 313÷29
- 92÷38
- 625÷3
- After biking 512 miles, Jada has traveled 23 of the length of her trip. How long (in miles) is the entire length of her trip? Write an equation to represent the situation, and then find the answer.
Are you ready for more?
Suppose you have a pint of grape juice and a pint of milk. You pour 1 tablespoon of the grape juice into the milk and mix it up. Then you pour 1 tablespoon of this mixture back into the grape juice. Which liquid is more contaminated?
Summary
The division a÷34=? is equivalent to 34⋅?=a, so we can think of it as meaning “34 of what number is a?” and represent it with a diagram as shown. The length of the entire diagram represents the unknown number.
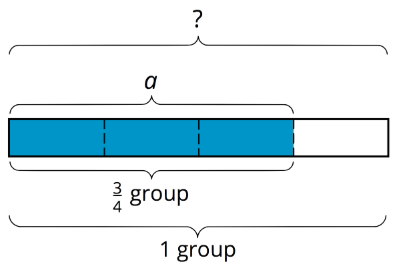
If 34 of a number is a, then to find the number, we can first divide a by 3 to find 14 of the number. Then we multiply the result by 4 to find the number.
The steps above can be written as: a÷3⋅4. Dividing by 3 is the same as multiplying by 13, so we can also write the steps as: a⋅13⋅4.
In other words: a÷3⋅4=a⋅13⋅4. And a⋅13⋅4=a⋅43, so we can say that:
a÷34=a⋅43
In general, dividing a number by a fraction cd is the same as multiplying the number by dc, which is the reciprocal of the fraction.
Glossary Entries
Definition: Reciprocal
Dividing 1 by a number gives the reciprocal of that number. For example, the reciprocal of 12 is 112, and the reciprocal of 25 is 52.
Practice
Exercise 23.2.4
Select all the statements that show correct reasoning for finding 1415÷75.
- Multiplying 1415 by 5 and then by 17.
- Dividing 1415 by 5, and then multiplying by 17.
- Multiplying 1415 by 7, and then multiplying by 15.
- Multiplying 1415 by 5 and then dividing by 7.
- Multiplying 1514 by 7 and then dividing by 5.
Exercise 23.2.5
Clare said that 43÷52 is 103. She reasoned: 43⋅5=203 and 203÷2=103.
Explain why Clare’s answer and reasoning are incorrect. Find the correct quotient.
Exercise 23.2.6
Find the value of 154÷58. Show your reasoning.
Exercise 23.2.7
Consider the problem: Kiran has 234 pounds of flour. When he divides the flour into equal-sized bags, he fills 418 bags. How many pounds fit in each bag?
Write a multiplication equation and a division equation to represent the question. Then, find the answer and show your reasoning.
Exercise 23.2.8
Divide 412 by each of these unit fractions.
- 18
- 14
- 16
(From Unit 4.3.1)
Exercise 23.2.9
Consider the problem: After charging for 13 of an hour, a phone is at 25 of its full power. How long will it take the phone to charge completely?
Decide whether each equation can represent the situation.
- 13⋅?=25
- 13÷25=?
- 25÷13=?
- 25⋅?=13
(From Unit 4.2.6)
Exercise 23.2.10
Elena and Noah are each filling a bucket with water. Noah’s bucket is 25 full and the water weighs 212 pounds. How much does Elena’s water weigh if her bucket is full and her bucket is identical to Noah’s?
- Write multiplication and division equations to represent the question.
- Draw a diagram to show the relationship between the quantities and to find the answer.
(From Unit 4.2.5)

