24.3: Fractional Lengths in Triangles and Prisms

Lesson

Let's explore area and volume when fractions are involved.

Exercise $\PageIndex{1}$: Area of Triangle

Find the area of Triangle A in square centimeters. Show your reasoning.

Figure $\PageIndex{1}$: A triangle labeled A with a vertical side. One vertex is to the left of the vertical side. A dashed horizontal line is drawn from the first vertex to the vertical side of the triangle and a right angle symbol is indicated. The dashed line and the vertical side are both labeled 4 and one half centimeters.

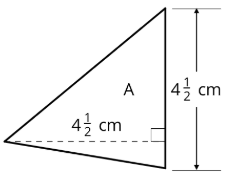
Exercise $\PageIndex{2}$: Bases and Heights of Triangles

1. The area of Triangle B is $8$ square units. Find the length of $b$. Show your reasoning.

Figure $\PageIndex{2}$: A triangle labeled B has a horizontal side on the bottom of the triangle and a vertex above the horizontal side. A dashed line is drawn from the vertex to the horizontal side and a right angle symbol is indicated. The horizontal side is labeled lowercase b and the dashed line is labeled eight thirds.

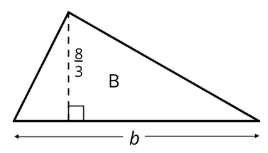
2. The area of Triangle C is $\frac{54}{5}$ square units. What is the length of $h$? Show your reasoning.

Figure $\PageIndex{3}$: A triangle labeled C has a horizontal side at the top of the triangle and a vertex below the horizontal side and to the left. A horizontal line extends from the horizontal side and to the left. A vertical dashed line is drawn from the bottom vertex to the extended horizontal line and a right angle symbol is indicated. The dashed line is labeled h and the horizontal side of the triangle is labeled 3 and three fifths.

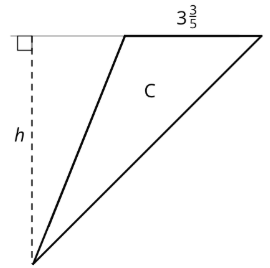
Exercise $\PageIndex{3}$: Volumes of Cubes and Prisms

Use cubes or the applet to help you answer the following questions.

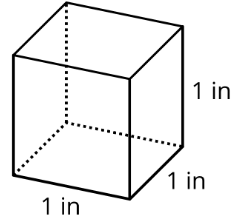
1. Here is a drawing of a cube with edge lengths of 1 inch.
   1. How many cubes with edge lengths of $\frac{1}{2}$ inch are needed to fill this cube?
   2. What is the volume, in cubic inches, of a cube with edge lengths of $\frac{1}{2}$ inch? Explain or show your reasoning.

Figure $\PageIndex{4}$

2. Four cubes are piled in a single stack to make a prism. Each cube has an edge length of $\frac{2}{2}$ inch. Sketch the prism, and find its volume in cubic inches.
3. Use cubes with an edge length of $\frac{1}{2}$ inch to build prisms with the lengths, widths, and heights shown in the table.
   1. For each prism, record in the table how many $\frac{1}{2}$-inch cubes can be packed into the prism and the volume of the prism.

      Table $\PageIndex{1}$

      prism length (in)	prism width (in)	prism height (in)	number of $\frac{1}{2}$-inch cubes in prism	volume of prism (in^3)
      $\frac{1}{2}$	$\frac{1}{2}$	$\frac{1}{2}$
      $1$	$1$	$\frac{1}{2}$
      $2$	$1$	$\frac{1}{2}$
      $2$	$2$	$1$
      $4$	$2$	$\frac{3}{2}$
      $5$	$4$	$2$
      $5$	$4$	$2\frac{1}{2}$

   2. Examine the values in the table. What do you notice about the relationship between the edge lengths of each prism and its volume?
4. What is the volume of a rectangular prism that is $1\frac{1}{2}$ inches by $2\frac{1}{4}$ inches by $4$ inches? Show your reasoning.

Are you ready for more?

A unit fraction has a $1$ in the numerator.

• These are unit fractions: $\frac{1}{3}, \frac{1}{100}, \frac{1}{1}$.
• These are not unit fractions: $\frac{2}{9},\frac{8}{1}, 2\frac{1}{5}$.

1. Find three unit fractions whose sum is $\frac{1}{2}$. An example is: $\frac{1}{8}+\frac{1}{8}+\frac{1}{4}=\frac{1}{2}$ How many examples like this can you find?
2. Find a box whose surface area in square units equals its volume in cubic units. How many like this can you find?

Summary

If a rectangular prism has edge lengths of 2 units, 3 units, and 5 units, we can think of it as 2 layers of unit cubes, with each layer having $(3\cdot 5)$ unit cubes in it. So the volume, in cubic units, is: $2\cdot 3\cdot 5$

Figure $\PageIndex{5}$

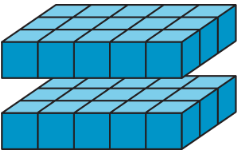
To find the volume of a rectangular prism with fractional edge lengths, we can think of it as being built of cubes that have a unit fraction for their edge length. For instance, if we build a prism that is $\frac{1}{2}$-inch tall, $\frac{3}{2}$-inch wide, and 4 inches long using cubes with a $\frac{1}{2}$-inch edge length, we would have:

• A height of 1 cube, because $1\cdot\frac{1}{2}=\frac{1}{2}$.
• A width of 3 cubes, because $3\cdot\frac{1}{2}=\frac{3}{2}$.
• A length of 8 cubes, because $8\cdot\frac{1}{2}=4$.

The volume of the prism would be $1\cdot 3\cdot 8$, or 24 cubic units. How do we find its volume in cubic inches? We know that each cube with a $\frac{1}{2}$-inch edge length has a volume of $\frac{1}{8}$ cubic inch, because $\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{8}$. Since the prism is built using $24$ of these cubes, its volume, in cubic inches, would then be $24\cdot\frac{1}{8}$, or $3$ cubic inches.

The volume of the prism, in cubic inches, can also be found by multiplying the fractional edge lengths in inches: ​​​​​​ $\frac{1}{2}\cdot\frac{3}{2}\cdot 4=3$

Practice

Exercise $\PageIndex{4}$

Clare is using little wooden cubes with edge length $\frac{1}{2}$ inch to build a larger cube that has edge length 4 inches. How many little cubes does she need? Explain your reasoning.

Exercise $\PageIndex{5}$

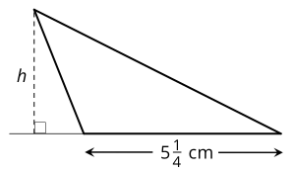
The triangle has an area of $7\frac{7}{8}$ cm² and a base of $5\frac{1}{4}$ cm.

What is the length of $h$? Explain your reasoning.

Figure $\PageIndex{6}$: A triangle with a horizontal base labeled five and one fourth centimeters. A vertex is above and to the left of the horizontal side and a horizontal line is extended to the left from the base. A vertical dashed line is drawn from the top vertex to the extended base and a right angle symbol is indicated. The vertical dashed line is labeled h.

Exercise $\PageIndex{6}$

1. Which expression can be used to find how many cubes with edge length of $\frac{1}{3}$ unit fit in a prism that is 5 units by 5 units by 8 units? Explain or show your reasoning.
   • $\left(5\cdot\frac{1}{3}\right)\cdot\left( 5\cdot\frac{1}{3}\right)\cdot\left( 8\cdot\frac{1}{3}\right)$
   • $5\cdot 5\cdot 8$
   • $\left( 5\cdot 3\right)\cdot\left( 5\cdot 3\right)\cdot\left( 8\cdot 3\right)$
   • $\left(5\cdot 5\cdot 8\right)\cdot\left(\frac{1}{3}\right)$
2. Mai says that we can also find the answer by multiplying the edge lengths of the prism and then multiplying the result by $27$. Do you agree with her? Explain your reasoning.

Exercise $\PageIndex{7}$

A builder is building a fence with $6\frac{1}{4}$-inch-wide wooden boards, arranged side-by-side with no gaps or overlaps. How many boards are needed to build a fence that is 150 inches long? Show your reasoning.

(From Unit 4.4.1)

Exercise $\PageIndex{8}$

Find the value of each expression. Show your reasoning and check your answer.

1. $2\frac{1}{7}\div\frac{2}{7}$
2. $\frac{17}{20}\div\frac{1}{4}$

(From Unit 4.4.1)

Exercise $\PageIndex{9}$

Consider the problem: A bucket contains $11\frac{2}{3}$ gallons of water and is $\frac{5}{6}$ full. How many gallons of water would be in a full bucket?

Write a multiplication and a division equation to represent the situation. Then, find the answer and show your reasoning.

(From Unit 4.3.2)

Exercise $\PageIndex{10}$

There are 80 kids in a gym. 75% are wearing socks. How many are not wearing socks? If you get stuck, consider using a tape diagram.

(From Unit 3.4.3)

Exercise $\PageIndex{11}$

1. Lin wants to save $75 for a trip to the city. If she has saved $37.50 so far, what percentage of her goal has she saved? What percentage remains?
2. Noah wants to save $60 so that he can purchase a concert ticket. If he has saved $45 so far, what percentage of his goal has he saved? What percentage remains?

(From Unit 3.4.2)