27.2: Adding and Subtracting Decimals with Few Non-Zero Digits

Last updated
Save as PDF

Page ID: 40300

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's add and subtract decimals.

Exercise $\PageIndex{1}$: Do the Zeros Matter?

Evaluate mentally: $1.009+0.391$
Decide if each equation is true or false. Be prepared to explain your reasoning.
1. $34.56000=34.56$
2. $25=25.0$
3. $2.405=2.45$

Exercise $\PageIndex{2}$: Calculating Sums

Andre and Jada drew base-ten diagrams to represent $0.007+0.004$. Andre drew 11 small rectangles. Jada drew only two figures: a square and a small rectangle.

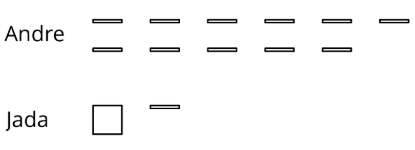
If both students represented the sum correctly, what value does each small rectangle represent? What value does each square represent?
Draw or describe a diagram that could represent the sum $0.008+0.07$.

Here are two calculations of $0.2+0.05$. Which is correct? Explain why one is correct and the other is incorrect.

Figure $\PageIndex{2}$: Two calculations of zero point 2 plus zero point zero five are indicated. The calculation on the left adds zero point 2 and zero point zero 5 by aligning the ones units, tenths unit, and hundredths unit. The sum is zero point 2 5. The calculation on the right adds zero point 2 and zero point zero five by aligning the hundredths unit under the tenths unit. The sum is zero point zero 7.

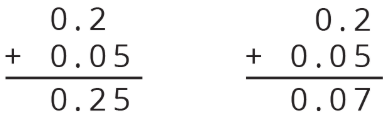
Compute each sum. If you get stuck, consider drawing base-ten diagrams to help you.

$0.209+0.01$
$10.2+1.1456$

The applet has tools that create each of the base-ten blocks. This time you need to decide the value of each block before you begin.
Select a Block tool, and then click on the screen to place it.
Click on the Move tool (the arrow) when you are done choosing blocks.
Subtract by deleting with the delete tool (the trash can), not by crossing out.

Exercise $\PageIndex{3}$: Subtracting Decimals of Different Lengths

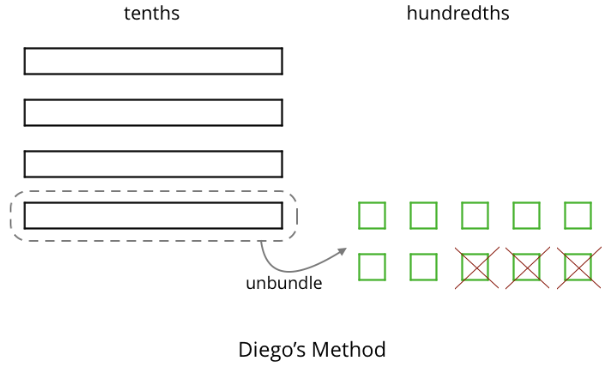
To represent $0.4-0.03$, Diego and Noah drew different diagrams. Each rectangle represented 0.1. Each square represented 0.01.

Diego started by drawing 4 rectangles to represent 0.4. He then replaced 1 rectangle with 10 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 3 rectangles and 7 squares in his diagram.

Figure $\PageIndex{4}$: A base-ten diagram labeled Diego's Method. There are 2 columns for the diagram. The first column header is labeled tenths and there are 4 rectangles. The second column header is labeled hundredths and there are 10 squares in that column. The last rectangle is circled with a dashed line and an arrow pointing from the rectangle to the column of squares is labeled unbundle. The last three squares are crossed out.

Noah started by drawing 4 rectangles to represent 0.4. He then crossed out 3 of rectangles to represent the subtraction, leaving 1 rectangle in his diagram.

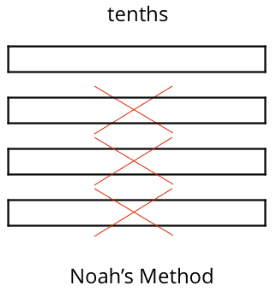
Do you agree that either diagram correctly represents $0.4-0.03$? Discuss your reasoning with a partner.
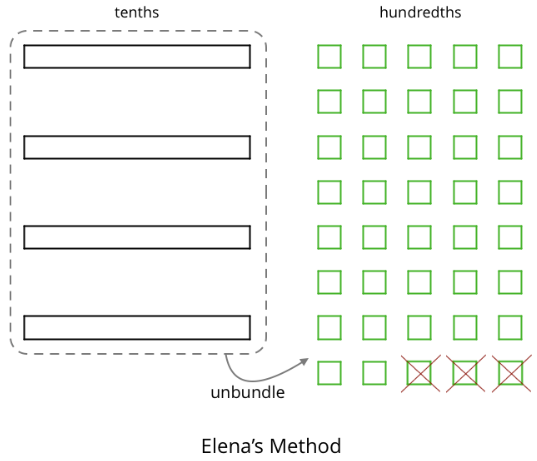
To represent $0.4-0.03$, Elena drew another diagram. She also started by drawing 4 rectangles. She then replaced all 4 rectangles with 40 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 37 squares in her diagram. Is her diagram correct? Discuss your reasoning with a partner.

Figure $\PageIndex{6}$:A base-ten diagram labeled Elena's Method. There are 2 columns for the diagram. The first column header is labeled tenths and there are 4 rectangles. The second column header is labeled hundredths and there are 40 squares in that column. All four rectangles are circled with a dashed line and an arrow pointing from the rectangles to the column of squares is labeled unbundle. The last three squares are crossed out.

Find each difference. If you get stuck, you can use the applet to represent each expression and find its value.
1. $0.3-0.05$
2. $2.1-0.4$
3. $1.03-0.06$
4. $0.02-0.007$

Be prepared to explain your reasoning.

The applet has tools that create each of the base-ten blocks. This time you need to decide the value of each block before you begin.
Select a Block tool, and then click on the screen to place it.
Click on the Move tool (the arrow) when you are done choosing blocks.
Subtract by deleting with the delete tool (the trash can), not by crossing out.

Are you ready for more?

A distant, magical land uses jewels for their bartering system. The jewels are valued and ranked in order of their rarity. Each jewel is worth 3 times the jewel immediately below it in the ranking. The ranking is red, orange, yellow, green, blue, indigo, and violet. So a red jewel is worth 3 orange jewels, a green jewel is worth 3 blue jewels, and so on.

At the Auld Shoppe, a shopper buys items that are worth 2 yellow jewels, 2 green jewels, 2 blue jewels, and 1 indigo jewel. If they came into the store with 1 red jewel, 1 yellow jewel, 2 green jewels, 1 blue jewel, and 2 violet jewels, what jewels do they leave with? Assume the shopkeeper gives them their change using as few jewels as possible.

Summary

Base-ten diagrams can help us understand subtraction as well. Suppose we are finding $0.23-0.07$. Here is a diagram showing 0.23, or 2 tenths and 3 hundredths.

Subtracting 7 hundredths means removing 7 small squares, but we do not have enough to remove. Because 1 tenth is equal to 10 hundredths, we can “unbundle” (or decompose) one of the tenths (1 rectangle) into 10 hundredths (10 small squares).

Figure $\PageIndex{8}$: Base ten diagram. 0 point 23. Two rectangles in the tenths column. 3 small squares in the hundredths column. A dotted rectangle is drawn around one of the rectangles with an arrow to 10 small squares. The arrow is labeled unbundle.

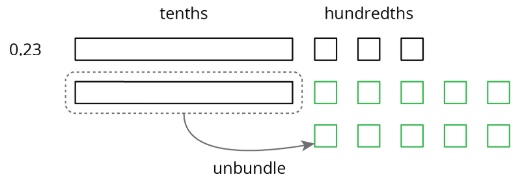
We now have 1 tenth and 13 hundredths, from which we can remove 7 hundredths.

Figure $\PageIndex{9}$: Base ten diagram. 0 point 23. One rectangle in the tenths column. 13 small squares in the hundredths column. 7 small squares have an X through them. The words subtract 0 point 0 7 is below the small squares.

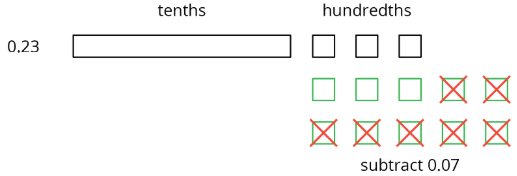
We have 1 tenth and 6 hundredths remaining, so $0.23-0.07=0.16$.

Here is a vertical calculation of $0.23-0.07$.

Figure $\PageIndex{11}$: Vertical subtraction. First line. 0 point 23. The 2 is crossed out and has a 1 above it. The 3 is crossed out and has 13 above it. Second line. Minus 0 point 0 0 7. Horizontal line. Third line. 0 point 17.

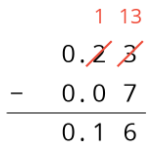
Notice how this representation also shows a tenth is unbundled (or decomposed) into 10 hundredths in order to subtract 7 hundredths.

This works for any decimal place. Suppose we are finding $0.023-0.007$. Here is a diagram showing $0.023$.

We want to remove 7 thousandths (7 small rectangles). We can “unbundle” (or decompose) one of the hundredths into 10 thousandths.

Figure $\PageIndex{13}$: Base 10 diagram. 0 point 0 2 3. Two small squares in the hundredths column. Three small rectangles in the thousandths column. A square is drawn around 1 small square. An arrow is drawn to 10 small rectangles. The arrow is labeled bundle.

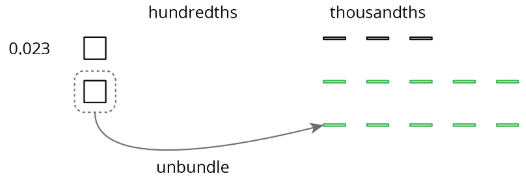
Now we can remove 7 thousandths.

Figure $\PageIndex{14}$: Base 10 diagram. 0 point 0 2 3. One small square in the hundredths column. 13 small rectangles in the thousandths column. 7 small rectangles have an X through them. Below the small rectangles are the words subtract 0 point 0 0 7.

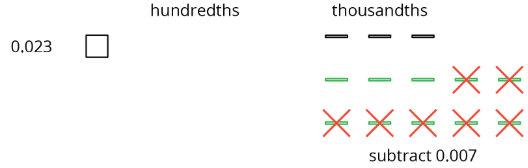
We have 1 hundredth and 6 thousandths remaining, so $0.023-0.007=0.016$.

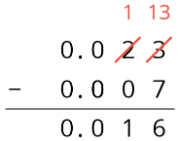
Here is a vertical calculation of $0.023-0.007$.

Figure $\PageIndex{16}$: Vertical subtraction. First line. 0 point 0 2 3. The 2 is crossed out and has a 1 above it. The 3 is crossed out and has 13 above it. Second line. Minus 0 point 0 0 7. Horizontal line. Third line. 0 point 0 1 6.

Practice

Exercise $\PageIndex{4}$

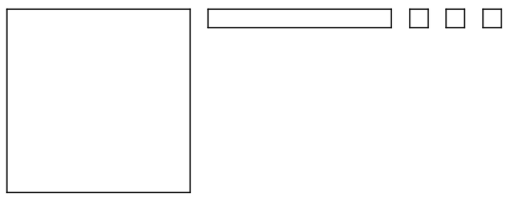
Here is a base-ten diagram that represents 1.13. Use the diagram to find $1.13-0.46$.

Explain or show your reasoning.

Exercise $\PageIndex{5}$

Compute the following sums. If you get stuck, consider drawing base-ten diagrams.

$0.027+0.004$
$0.203+0.01$
$1.2+0.145$

Exercise $\PageIndex{6}$

A student said we cannot subtract 1.97 from 20 because 1.97 has two decimal digits and 20 has none. Do you agree with him? Explain or show your reasoning.

Exercise $\PageIndex{7}$

Decide which calculation shows the correct way to find $0.3-0.006$ and explain your reasoning.

Figure $\PageIndex{18}$: 4 subtraction problems. problem a. 3 tenths - 6 thousandths = 306 thousandths. problem b. 3 tenths - 6 thousandths = 97 thousandths. problem c. 3 tenths - 6 thousandths = 24 thousandths. problem d. 3 tenths - 6 thousandths = 294 thousandths.

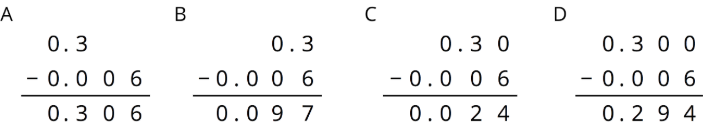
Exercise $\PageIndex{8}$

Complete the calculations so that each shows the correct difference.

Figure $\PageIndex{19}$: 3 decimal subtraction problems. Problem a. 14 and 6 tenths -1 and 4 tenths =blank blank blank point 2. Problem b. 38 and 60 hundredths -6 and 75 hundredths = blank blank point blank 5. Problem c. 241 and 76 hundredths -2 and 18 hundredths = blank blank blank point blank 8.

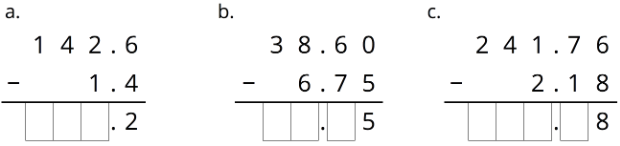
Exercise $\PageIndex{9}$

The school store sells pencils for $0.30 each, hats for $14.50 each, and binders for $3.20 each. Elena would like to buy 3 pencils, a hat, and 2 binders. She estimated that the cost will be less than $20.

Do you agree with her estimate? Explain your reasoning.
Estimate the number of pencils could she buy with $5. Explain or show your reasoning.

(From Unit 5.1.1)

Exercise $\PageIndex{10}$

A rectangular prism measures $7\frac{1}{2}$ cm by $12$ cm by $15\frac{1}{2}$ cm.

Calculate the number of cubes with edge length $\frac{1}{2}$ cm that fit in this prism.
What is the volume of the prism in $\text{cm}^{3}$? Show your reasoning. If you are stuck, think about how many cubes with $\frac{1}{2}$-cm edge lengths fit into $1\text{ cm}^{2}$.

(From Unit 4.4.4)

Exercise $\PageIndex{11}$

At a constant speed, a car travels 75 miles in 60 minutes. How far does the car travel in 18 minutes? If you get stuck, consider using the table.

Table $\PageIndex{1}$
minutes	distance in miles
$60$	$75$
$6$
$18$

(From Unit 2.4.2)

minutes	distance in miles
\(60\)	\(75\)
\(6\)
\(18\)

Search

Text Color

Text Size

Margin Size

Font Type