28.2: Methods for Multiplying Decimals

Last updated
Save as PDF

Page ID: 40304

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's look at some ways we can represent multiplication of decimals.

Exercise $\PageIndex{1}$: Equivalent Expressions

Write as many expressions as you can think of that are equal to 0.6. Do not use addition or subtraction.

Exercise $\PageIndex{2}$: Using Properties of Numbers to Reason about Multiplication

Elena and Noah used different methods to compute $(0.23)\cdot (1.5)$. Both calcuations were correct.

Figure $\PageIndex{1}$: Elena's method. 0 point 2 3 times 100 equals 23. 1 point 5 times 10 equals 15. 23 times 15 equals 345. 345 divided by 1000 equals 0 point 3 4 5. Noah's method. 0 point 2 3 equals the fraction 23 over 100. 1 point 5 equals the fraction 15 over 10. The fraction 23 over 100 times the fraction 15 over 10 equals the fractions 345 over 1000. The fraction 345 over 1000 equals 0 point 3 4 5.

Analyze the two methods, then discuss these questions with your partner.
- Which method makes more sense to you? Why?
- What might Elena do to compute $(0.16)\cdot (0.03)$? What might Noah do to compute $(0.16)\cdot (0.03)$? Will the two methods result in the same value?
Compute each product using the equation $21\cdot 47=987$ and what you know about fractions, decimals, and place value. Explain or show your reasoning.
1. $(2.1)\cdot (4.7)$
2. $21\cdot (0.047)$
3. $(0.021)\cdot (4.7)$

Exercise $\PageIndex{3}$: Using Area Diagrams to Reason about Multiplication

In the diagram, the side length of each square is 0.1 unit.

Explain why the area of each square is not 0.1 square unit.

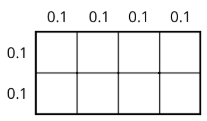
How can you use the area of each square to find the area of the rectangle? Explain or show your reasoning.
Explain how the diagram shows that the equation $(0.4)\cdot (0.2)=0.08$ is true.

Label the squares with their side lengths so the area of this rectangle represents $40\cdot 20$.

What is the area of each square?
Use the squares to help you find $40\cdot 20$. Explain or show your reasoning.

Label the squares with their side lengths so the area of this rectangle represents $(0.04)\cdot (0.02)$.
Next, use the diagram to help you find $(0.04)\cdot (0.02)$. Explain or show your reasoning.

Summary

Here are three other ways to calculate a product of two decimals such as $(0.04)\cdot (0.07)$.

First, we can multiply each decimal by the same power of 10 to obtain whole-number factors.

$\begin{aligned} (0.04)\cdot 100&=4 \\ (0.07)\cdot 100&=7 \\ 4\cdot 7&=28\end{aligned}$

Because we multiplied both 0.04 and 0.07 by 100 to get 4 and 7, the product 28 is $(100\cdot 100)$ times the original product, so we need to divide 28 by 10,000.

$28\div 10,000=0.0028$

Second, we can write each decimal as a fraction, $0.04=\frac{4}{100}$ and $0.07=\frac{7}{100}$, and multiply them.

$\frac{4}{100}\cdot\frac{7}{100}=\frac{28}{10,000}=0.0028$

Third, we can use an area model. The product $(0.04)\cdot (0.07)$ can be thought of as the area of a rectangle with side lengths of 0.04 unit and 0.07 unit.

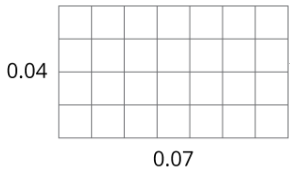
In this diagram, each small square is 0.01 unit by 0.01 unit. The area of each square, in square units, is therefore $\left(\frac{1}{100}\cdot\frac{1}{100}\right)$, which is $\frac{1}{10,000}$.

Because the rectangle is composed of 28 small squares, the area of the rectangle, in square units, must be:

$28\cdot\frac{1}{10,000}=\frac{28}{10,000}=0.0028$

All three calculations show that $(0.04)\cdot (0.07)=0.0028$.

Practice

Exercise $\PageIndex{4}$

Find each product. Show your reasoning.

$(1.2)\cdot (0.11)$
$(0.34)\cdot (0.02)$
$120\cdot (0.002)$

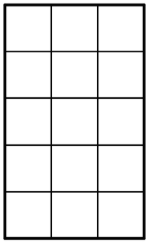
Exercise $\PageIndex{5}$

You can use a rectangle to represent $(0.3)\cdot (0.5)$.

What must the side length of each square represent for the rectangle to correctly represent $(0.3)\cdot (0.5)$?
What area is represented by each square?
What is $(0.3)\cdot (0.5)$? Show your reasoning.

Exercise $\PageIndex{6}$

One gallon of gasoline in Buffalo, New York costs $2.29. In Toronto, Canada, one liter of gasoline costs $0.91. There are 3.8 liters in one gallon.

How much does one gallon of gas cost in Toronto? Round your answer to the nearest cent.
Is the cost of gas greater in Buffalo or in Toronto? How much greater?

Exercise $\PageIndex{7}$

Calculate each sum or difference.

$10.3+3.7\qquad 20.99-4.97\qquad 15.99+23.51\qquad 1.893-0.353$

(From Unit 5.2.1)

Exercise $\PageIndex{8}$

Find the value of $\frac{49}{50}\div\frac{7}{6}$ using any method.

(From Unit 4.3.2)

Exercise $\PageIndex{9}$

Find the area of the shaded region. All angles are right angles. Show your reasoning.

Figure $\PageIndex{7}$: A multi-sided figure. The sides on top measure 10 units, 35 units, and 15 units. Two of the three sides on the left measure 10 units. One of the two sides on the right measures 10 units. One of the two sides on the bottom measure 15 units. The total width of the figure is 60 units, and the total height is 30 units. All angles are right angles.

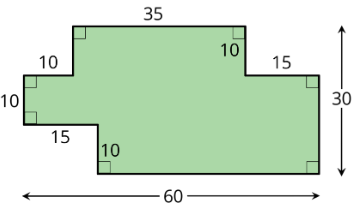
(From Unit 1.1.1)

Exercise $\PageIndex{10}$

Priya finds $(1.05)\cdot (2.8)$ by calculating $105\cdot 28$, then moving the decimal point three places to the left. Why does Priya’s method make sense?
Use Priya’s method to calculate $(1.05)\cdot (2.8)$. You can use the fact that $105\cdot 28=2,940$.
Use Priya’s method to calculate $(0.0015)\cdot (0.024)$.

Search

Text Color

Text Size

Margin Size

Font Type