29.1: Using the Partial Quotients Method
- Page ID
- 40310
Lesson
Let's divide whole numbers.
Exercise \(\PageIndex{1}\): Using Base-Ten Diagrams to Calculate Quotients
Elena used base-ten diagrams to find \(372\div 3\). She started by representing \(372\).
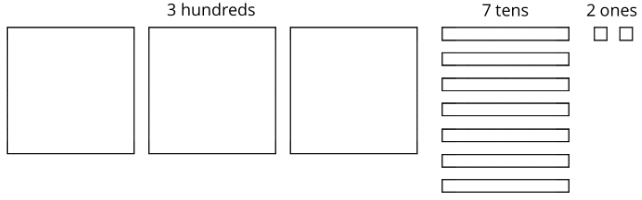
She made 3 groups, each with 1 hundred. Then, she put the tens and ones in each of the 3 groups. Here is her diagram for \(372\div 3\).
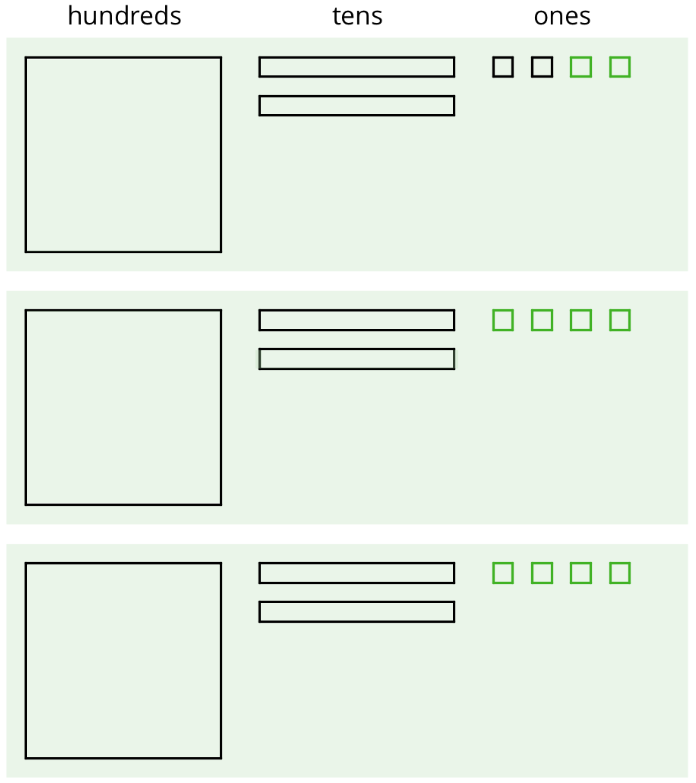
Discuss with a partner:
- Elena’s diagram for 372 has 7 tens. The one for \(372\div 3\) has only 6 tens. Why?
- Where did the extra ones (small squares) come from?
Exercise \(\PageIndex{2}\): Using the Partial Quotients Method to Calculate Quotients
- Andre calculated \(657\div 3\) using a method that was different from Elena’s.

- Andre subtracted 600 from 657. What does the 600 represent?
- Andre wrote 10 above the 200, and then subtracted 30 from 57. How is the 30 related to the 10?
- What do the numbers 200, 10, and 9 represent?
- What is the meaning of the 0 at the bottom of Andre’s work?
- How might Andre calculate \(896\div 4\)? Explain or show your reasoning.
Exercise \(\PageIndex{3}\): What's the Quotient?
- Find the quotient of \(1,332\div 9\) using one of the methods you have seen so far. Show your reasoning.
- Find each quotient and show your reasoning. Use the partial quotients method at least once.
- \(1,115\div 5\)
- \(665\div 7\)
- \(432\div 16\)
Summary
We can find the quotient \(345\div 3\) in different ways.
One way is to use a base-ten diagram to represent the hundreds, tens, and ones and to create equal-sized groups.
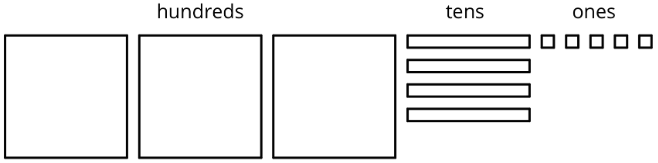
We can think of the division by 3 as splitting up 345 into 3 equal groups.
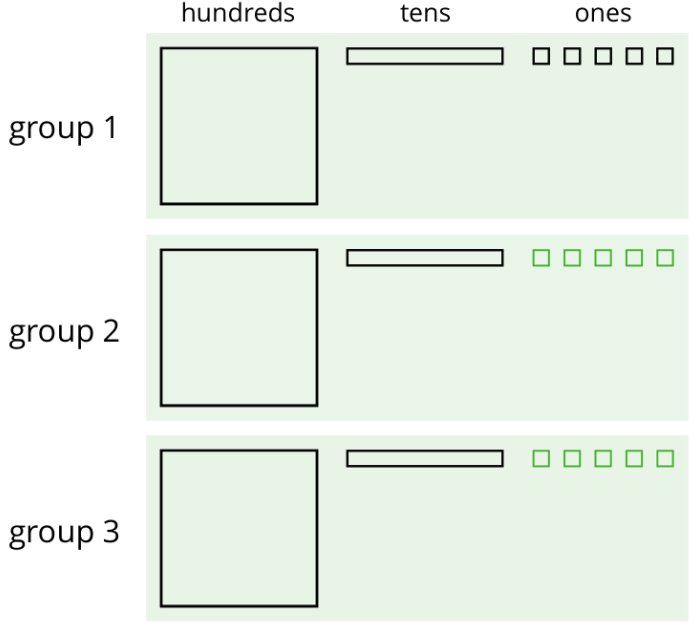
Each group has 1 hundred, 1 ten, and 5 ones, so \(345\div 3=115\). Notice that in order to split 345 into 3 equal groups, one of the tens had to be unbundled or decomposed into 10 ones.
Another way to divide 345 by 3 is by using the partial quotients method, in which we keep subtracting 3 groups of some amount from 345.

- In the calculation on the left, first we subtract 3 groups of 100, then 3 groups of 10, and then 3 groups of 5. Adding up the partial quotients (\(100+10+5\)) gives us 115.
- The calculation on the right shows a different amount per group subtracted each time (3 groups of 15, 3 groups of 50, and 3 more groups of 50), but the total amount in each of the 3 groups is still 115. There are other ways of calculating \(345\div 3\) using the partial quotients method.
Both the base-ten diagrams and partial quotients methods are effective. If, however, the dividend and divisor are large, as in \(1,248\div 26\), then the base-ten diagrams will be time-consuming.
Practice
Exercise \(\PageIndex{4}\)
Here is one way to find \(2,105\div 5\) using partial quotients. Show a different way of using partial quotients to divide 2,105 by 5.
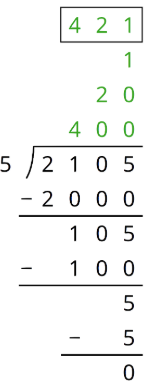
Exercise \(\PageIndex{5}\)
Andre and Jada both found \(657\div 3\) using the partial quotients method, but they did the calculations differently, as shown here.

- How is Jada's work the same as Andre’s work? How is it different?
- Explain why they have the same answer.
Exercise \(\PageIndex{6}\)
Which might be a better way to evaluate \(1,150\div 46\): drawing base-ten diagrams or using the partial quotients method? Explain your reasoning.
Exercise \(\PageIndex{7}\)
Here is an incomplete calculation of \(534\div 6\).
Write the missing numbers (marked with “?”) that would make the calculation complete.
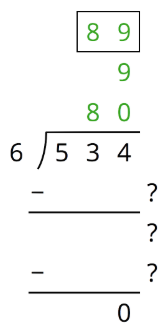
Exercise \(\PageIndex{8}\)
Use the partial quotients method to find \(1,032\div 43\).
Exercise \(\PageIndex{9}\)
Which of the polygons has the greatest area?
- A rectangle that is 3.25 inches wide and 6.1 inches long.
- A square with side length of 4.6 inches.
- A parallelogram with a base of 5.875 inches and a height of 3.5 inches.
- A triangle with a base of 7.18 inches and a height of 5.4 inches.
(From Unit 5.3.4)
Exercise \(\PageIndex{10}\)
One micrometer is a millionth of a meter. A certain spider web is 4 micrometers thick. A fiber in a shirt is 1 hundred-thousandth of a meter thick.
- Which is wider, the spider web or the fiber? Explain your reasoning.
- How many meters wider?
(From Unit 5.2.3)

