5.3: More Nets, More Surface Area
- Page ID
- 39644
Lesson
Let's draw nets and find the surface area of polyhedra.
Exercise \(\PageIndex{1}\): Notice and Wonder: Wrapping Paper
Kiran is wrapping this box of sports cards as a present for a friend.
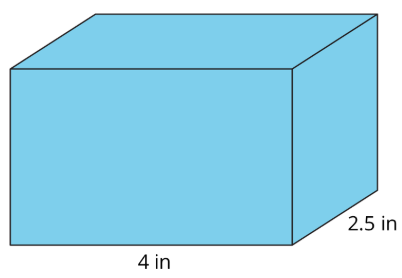
What do you notice? What do you wonder?
Exercise \(\PageIndex{2}\): Building Prisms and Pyramids
Your teacher will give you a drawing of a polyhedron. You will draw its net and calculate its surface area.
- What polyhedron do you have?
- Study your polyhedron. Then, draw its net on graph paper. Use the side length of a grid square as the unit.
- Label each polygon on the net with a name or number.
- Find the surface area of your polyhedron. Show your thinking in an organized manner so that it can be followed by others.
Exercise \(\PageIndex{3}\): Comparing Boxes
Here are the nets of three cardboard boxes that are all rectangular prisms. The boxes will be packed with 1-centimeter cubes. All lengths are in centimeters.
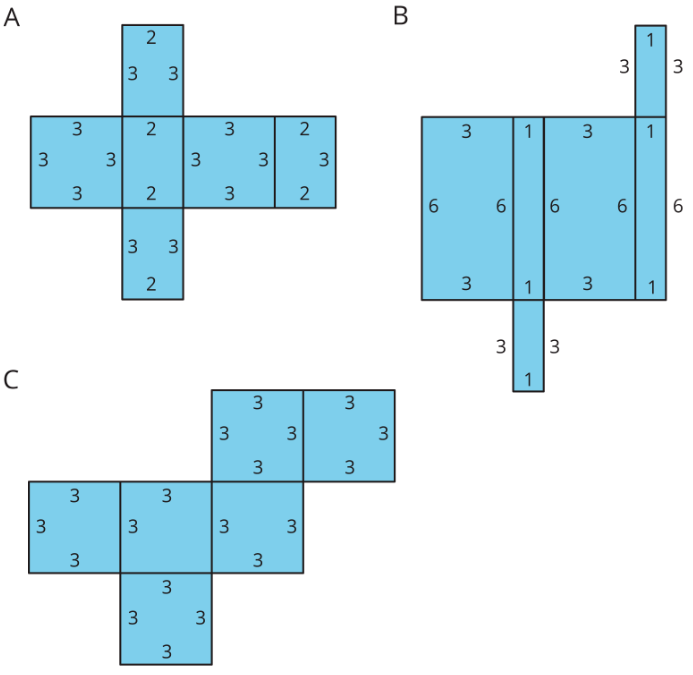
- Compare the surface areas of the boxes. Which box will use the least cardboard? Show your reasoning.
- Now compare the volumes of these boxes in cubic centimeters. Which box will hold the most 1-centimeter cubes? Show your reasoning.
Are you ready for more?
Figure C shows a net of a cube. Draw a different net of a cube. Draw another one. And then another one. How many different nets can be drawn and assembled into a cube?
Summary
The surface area of a polyhedron is the sum of the areas of all of the faces. Because a net shows us all faces of a polyhedron at once, it can help us find the surface area. We can find the areas of all polygons in the net and add them.
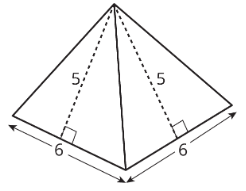
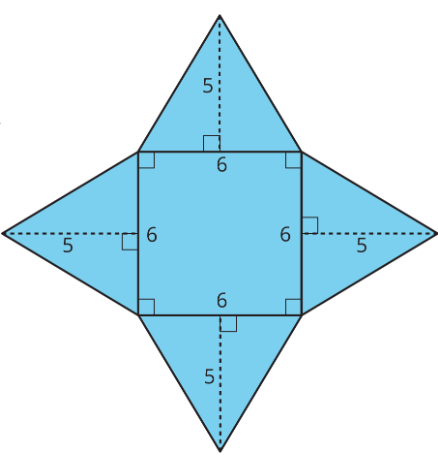
A square pyramid has a square and four triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces:
\((6\cdot 6)+4\cdot (\frac{1}{2}\cdot 5\cdot 6)=96\)
The surface area of this square pyramid is 96 square units.
Glossary Entries
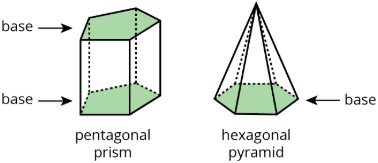
Definition: Base (of a Prism or Pyramid)
The word base can also refer to a face of a polyhedron.
A prism has two identical bases that are parallel. A pyramid has one base.
A prism or pyramid is named for the shape of its base.
Definition: Face
Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.
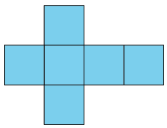
Definition: Net
A net is a two-dimensional figure that can be folded to make a polyhedron.
Here is a net for a cube.
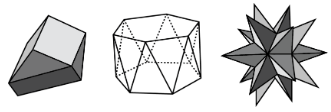
Definition: Polyhedron
A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.
Here are some drawings of polyhedra.
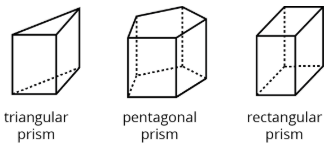
Definition: Prism
A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.
Here are some drawings of prisms.
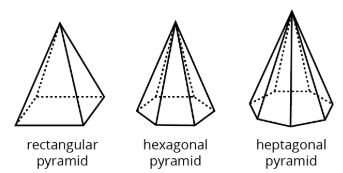
Definition: Pyramid
A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.
Here are some drawings of pyramids.
Definition: Surface Area
The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.
For example, if the faces of a cube each have an area of 9 cm2, then the surface area of the cube is \(6\cdot 9\), or 54 cm2.
Practice
Exercise \(\PageIndex{4}\)
Jada drew a net for a polyhedron and calculated its surface area.
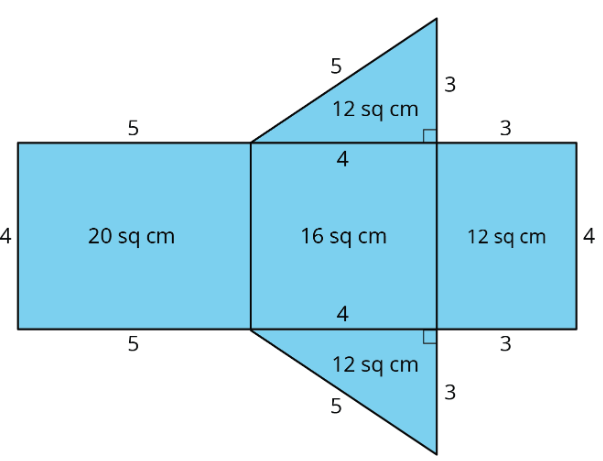
- What polyhedron can be assembled from this net?
- Jada made some mistakes in her area calculation. What were the mistakes?
- Find the surface area of the polyhedron. Show your reasoning.
Exercise \(\PageIndex{5}\)
A cereal box is 8 inches by 2 inches by 12 inches. What is its surface area? Show your reasoning. If you get stuck, consider drawing a sketch of the box or its net and labeling the edges with their measurements.
Exercise \(\PageIndex{6}\)
Twelve cubes are stacked to make this figure.

- What is its surface area?
- How would the surface area change if the top two cubes are removed?
(From Unit 1.5.1)
Exercise \(\PageIndex{7}\)
Here are two polyhedra and their nets. Label all edges in the net with the correct lengths.
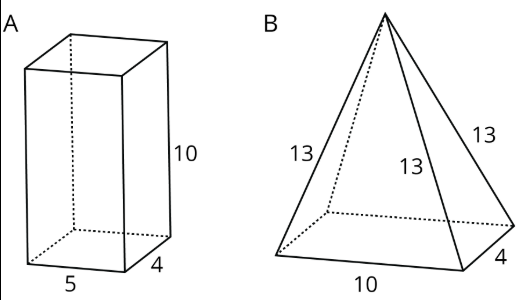
Exercise \(\PageIndex{8}\)
- What three-dimensional figure can be assembled from the net?
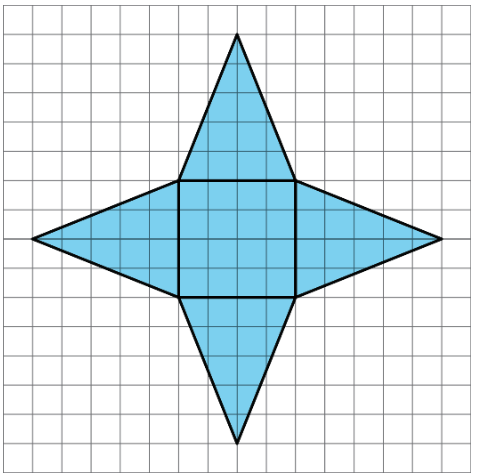
- What is the surface area of the figure? (One grid square is 1 square unit.)
(From Unit 1.5.3)


