5.2: Nets and Surface Area

Last updated

Mar 27, 2022
Save as PDF
- 5.1: Polyhedra
- 5.3: More Nets, More Surface Area

Illustrative Mathematics
OpenUp Resources

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's use nets to find the surface area of polyhedra.

Exercise $\PageIndex{1}$ : Matching Nets

Each of the nets can be assembled into a polyhedron. Match each net with its corresponding polyhedron, and name the polyhedron. Be prepared to explain how you know the net and polyhedron go together.

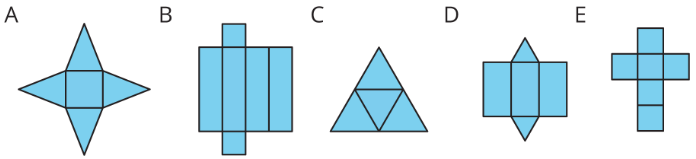
Exercise $\PageIndex{2}$ : Using Nets to Find Surface Area

Name the polyhedron that each net would form when assembled.

Figure $\PageIndex{3}$ : Three nets on a grid, labeled A, B, and C. Net A is composed of two rectangles that are 5 units tall by 6 units wide, two that are 5 units high and one unit wide, and two that are one unit high and six units wide. Net B is a square with a side length of 4 units and is surrounded by triangles that are four units wide at the base and four units high. Net C is a square with a side length of 3, a rectangle 3 units wide and 5 units high, another rectangle that is 3 units wide and 4 units tall, and two triangles, one on either side, that are three units tall by four units across.

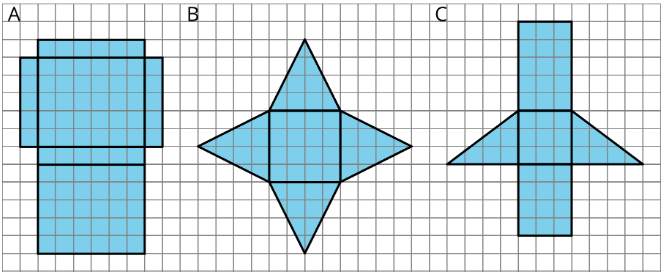
Your teacher will give you the nets of three polyhedra. Cut out the nets and assemble the three-dimensional shapes.
Find the surface area of each polyhedron. Explain your reasoning clearly.

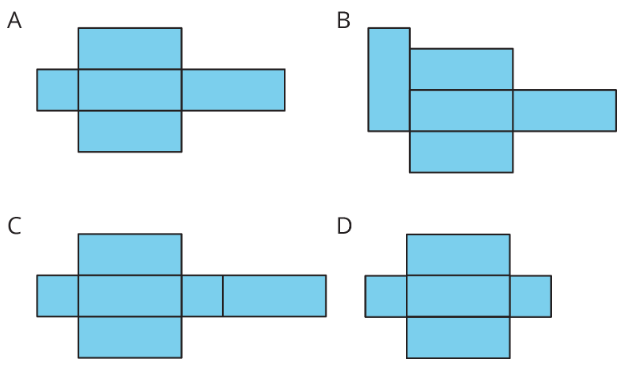
Are you ready for more?

For each net, decide if it can be assembled into a rectangular prism

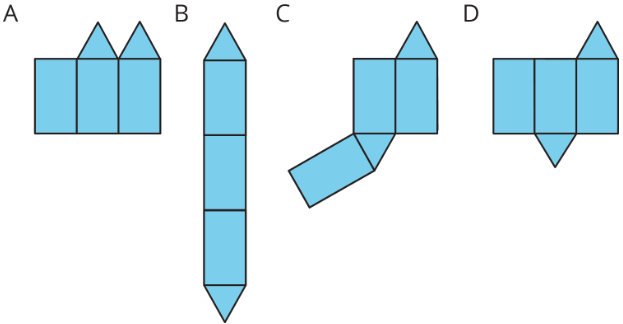
For each net, decide if it can be folded into a triangular prism.

Summary

A net of a pyramid has one polygon that is the base. The rest of the polygons are triangles. A pentagonal pyramid and its net are shown here.

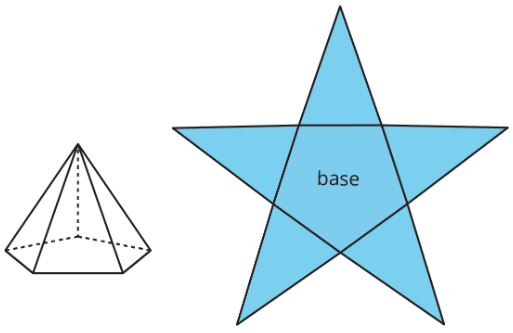
A net of a prism has two copies of the polygon that is the base. The rest of the polygons are rectangles. A pentagonal prism and its net are shown here.

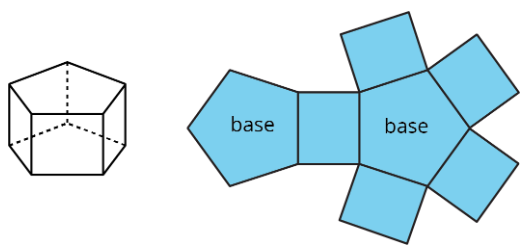
In a rectangular prism, there are three pairs of parallel and identical rectangles. Any pair of these identical rectangles can be the bases.

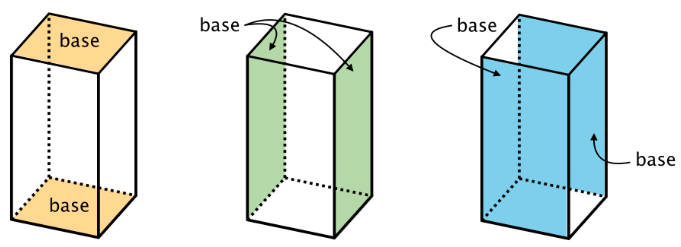
Because a net shows all the faces of a polyhedron, we can use it to find its surface area. For instance, the net of a rectangular prism shows three pairs of rectangles: 4 units by 2 units, 3 units by 2 units, and 4 units by 3 units.

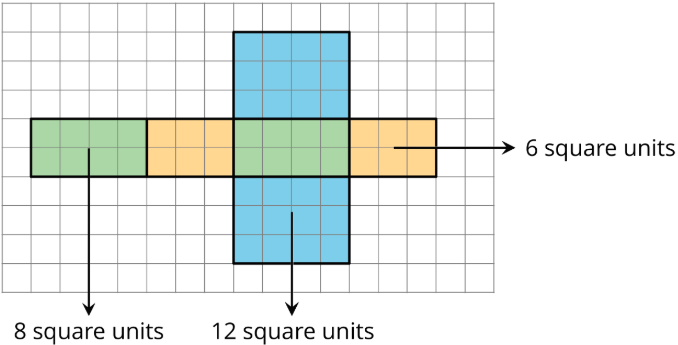
The surface area of the rectangular prism is 52 square units because $8+8+6+6+12+12=52$ .

Glossary Entries

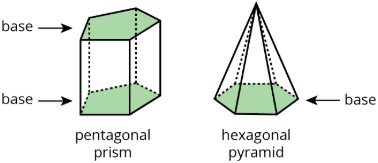
Definition: Base (of a Prism or Pyramid)

The word base can also refer to a face of a polyhedron.

A prism has two identical bases that are parallel. A pyramid has one base.

A prism or pyramid is named for the shape of its base.

Figure $\PageIndex{10}$ : The figure on the left is labeled pentagonal prism. There are two identical pentagons on the top and bottom. Each vertex of a pentagon is connected by a vertical segment to the corresponding vertex of the other pentagons. The pentagons are each shaded, with the word base pointing to each. The figure on the right is labeled hexagonal pyramid. There is a hexagon on the bottom shaded green. From a point above the hexagon extend 6 segments, each connected to a vertex of the hexagon.

Definition: Face

Each flat side of a polyhedron is called a face. For example, a cube has 6 faces, and they are all squares.

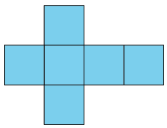
Definition: Net

A net is a two-dimensional figure that can be folded to make a polyhedron.

Here is a net for a cube.

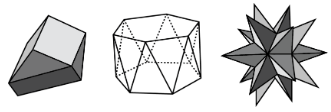
Definition: Polyhedron

A polyhedron is a closed, three-dimensional shape with flat sides. When we have more than one polyhedron, we call them polyhedra.

Here are some drawings of polyhedra.

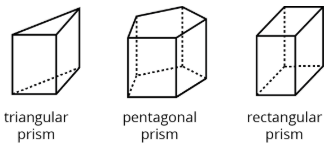
Definition: Prism

A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.

Here are some drawings of prisms.

Definition: Pyramid

A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.

Here are some drawings of pyramids.

Definition: Surface Area

The surface area of a polyhedron is the number of square units that covers all the faces of the polyhedron, without any gaps or overlaps.

For example, if the faces of a cube each have an area of 9 cm², then the surface area of the cube is $6\cdot 9$ , or 54 cm².

Practice

Exercise $\PageIndex{3}$

Can this net be assembled into a cube? Explain how you know. Label parts of the net with letters or numbers if it helps your explanation.

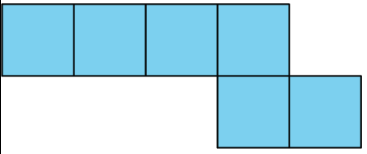
Exercise $\PageIndex{4}$

What polyhedron can be assembled from this net? Explain how you know.

Figure $\PageIndex{16}$ : Net on a grid. 3 adjacent rectangles, from left to right 4 by 5 units, 3 by 5 units, 5 by 5 units. above and below first rectangle are triangles with base = 4 units, height = 3 units.

Find the surface area of this polyhedron. Show your reasoning.

Exercise $\PageIndex{5}$

Here are two nets. Mai said that both nets can be assembled into the same triangular prism. Do you agree? Explain or show your reasoning.

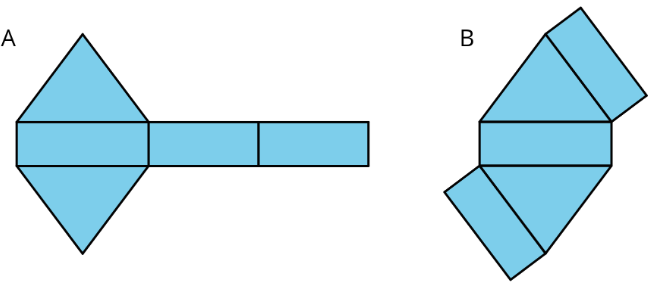
Exercise $\PageIndex{6}$

Here are two three-dimensional figures.

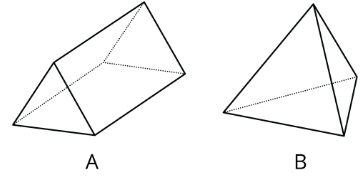
Tell whether each of the following statements describes Figure A, Figure B, both, or neither.

This figure is a polyhedron.
This figure has triangular faces.
There are more vertices than edges in this figure.
This figure has rectangular faces.
This figure is a pyramid.
There is exactly one face that can be the base for this figure.
The base of this figure is a triangle.
This figure has two identical and parallel faces that can be the base.

(From Unit 1.5.2)

Exercise $\PageIndex{7}$

Select all units that can be used for surface area.

square meters
feet
centimeters
cubic inches
square inches
square feet

(From Unit 1.5.1)

Exercise $\PageIndex{8}$

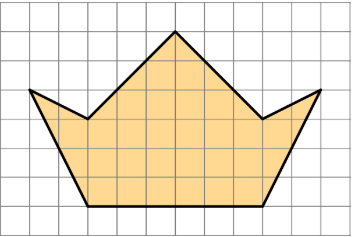
Find the area of this polygon. Show your reasoning.

(From Unit 1.4.1)

Search

Text Color

Text Size

Margin Size

Font Type

Lesson

Summary

Glossary Entries

Practice

Support Center

How can we help?