3.7: Multiply and Divide Integers (Part 1)
- Page ID
- 4987
- Multiply integers
- Divide integers
- Simplify expressions with integers
- Evaluate variable expressions with integers
- Translate word phrases to algebraic expressions
Before you get started, take this readiness quiz.
- Translate the quotient of \(20\) and \(13\) into an algebraic expression. If you missed this problem, review Example 1.5.12.
- Add: \(−5 + (−5) + (−5)\). If you missed this problem, review Example 3.2.8.
- Evaluate \(n + 4\) when \(n = −7\). If you missed this problem, review Example 3.2.10.
Multiply Integers
Since multiplication is mathematical shorthand for repeated addition, our counter model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction.
We remember that \(a • b\) means add \(a\), \(b\) times. Here, we are using the model shown in Figure \(\PageIndex{1}\) just to help us discover the pattern.
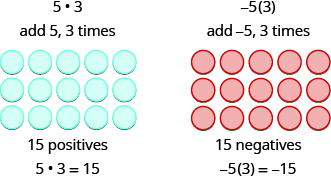
Figure \(\PageIndex{1}\)
Now consider what it means to multiply \(5\) by \(−3\). It means subtract \(5\), \(3\) times. Looking at subtraction as taking away, it means to take away \(5\), \(3\) times. But there is nothing to take away, so we start by adding neutral pairs as shown in Figure \(\PageIndex{2}\).
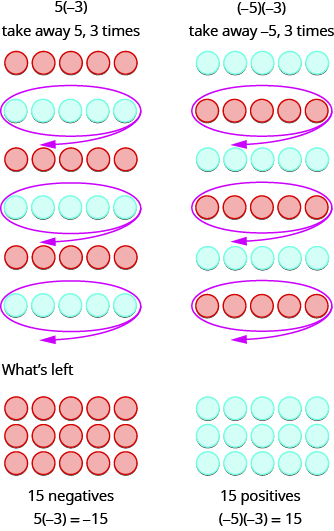
Figure \(\PageIndex{2}\)
In both cases, we started with \(15\) neutral pairs. In the case on the left, we took away \(5\), \(3\) times and the result was \(−15\). To multiply \((−5)(−3)\), we took away \(−5\), \(3\) times and the result was \(15\). So we found that
| 5(3) = 15 | -5(3) = -15 |
| 5(-3) = -15 | (-5)(-3) = 15 |
Notice that for multiplication of two signed numbers, when the signs are the same, the product is positive, and when the signs are different, the product is negative.
The sign of the product of two numbers depends on their signs.
| Same signs | Product |
|---|---|
| Two positives | Positive |
| Two negatives | Positive |
| Different signs | Product |
|---|---|
| Positive • negative | Negative |
| Negative • positive | Negative |
Multiply each of the following:
- \(−9 • 3\)
- \(−2(−5)\)
- \(4(−8)\)
- \(7 • 6\)
Solution
| Multiply, noting that the signs are different and so the product is negative. | –9 • 3 = –27 |
| Multiply, noting that the signs are the same and so the product is positive. | –2(–5) = 10 |
| Multiply, noting that the signs are different and so the product is negative. | 4(–8) = –32 |
| The signs are the same, so the product is positive. | 7 • 6 = 42 |
Multiply:
- \(−6 • 8\)
- \(−4(−7)\)
- \(9(−7)\)
- \(5 • 12\)
- Answer a
-
\(-48\)
- Answer b
-
\(28\)
- Answer c
-
\(-63\)
- Answer d
-
\(60\)
Multiply:
- \(−8 • 7\)
- \(−6(−9)\)
- \(7(−4)\)
- \(3 • 13\)
- Answer a
-
\(-56\)
- Answer b
-
\(54\)
- Answer c
-
\(-28\)
- Answer d
-
\(39\)
When we multiply a number by \(1\), the result is the same number. What happens when we multiply a number by \(−1\)? Let’s multiply a positive number and then a negative number by \(−1\) to see what we get.
| −1 • 4 | −1(−3) |
| −4 | 3 |
| −4 is the opposite of 4 | 3 is the opposite of −3 |
Each time we multiply a number by \(−1\), we get its opposite.
Multiplying a number by \(−1\) gives its opposite.
\[-1 \cdot a = -a \]
Multiply each of the following:
- \(−1 • 7\)
- \(−1(−11)\)
Solution
| The signs are different, so the product will be negative. | −1 • 7 |
| Notice that −7 is the opposite of 7. | −7 |
| The signs are the same, so the product will be positive. | −1(−11) |
| Notice that 11 is the opposite of −11. | 11 |
Multiply.
- \(−1 • 9\)
- \(−1 • (−17)\)
- Answer a
-
\(-9\)
- Answer b
-
\(17\)
Multiply.
- \(−1 • 8\)
- \(−1 • (−16)\)
- Answer a
-
\(-8\)
- Answer b
-
\(16\)
Divide Integers
Division is the inverse operation of multiplication. So, \(15 ÷ 3 = 5\) because \(5 • 3 = 15\) In words, this expression says that \(15\) can be divided into \(3\) groups of \(5\) each because adding five three times gives \(15\). If we look at some examples of multiplying integers, we might figure out the rules for dividing integers.
| 5 • 3 = 15 so 15 ÷ 3 = 5 | −5(3) = −15 so −15 ÷ 3 = −5 |
| (−5)(−3) = 15 so 15 ÷ (−3) = −5 | 5(−3) = −15 so −15 ÷ −3 = 5 |
Division of signed numbers follows the same rules as multiplication. When the signs are the same, the quotient is positive, and when the signs are different, the quotient is negative.
The sign of the quotient of two numbers depends on their signs.
| Same signs | Quotient |
|---|---|
| Two positives | Positive |
| Two negatives | Positive |
| Different signs | Quotient |
|---|---|
| Positive & negative | Negative |
| Negative & positive | Negative |
Remember, you can always check the answer to a division problem by multiplying.
Divide each of the following:
- \(−27 ÷ 3\)
- \(−100 ÷ (−4)\)
Solution
| Divide, noting that the signs are different and so the quotient is negative. | –27 ÷ 3 = –9 |
| Divide, noting that the signs are the same and so the quotient is positive. | –100 ÷ (–4) = 25 |
Divide:
- \(−42 ÷ 6\)
- \(−117 ÷ (−3)\)
- Answer a
-
\(-7\)
- Answer b
-
\(39\)
Divide:
- \(−63 ÷ 7\)
- \(−115 ÷ (−5)\)
- Answer a
-
\(-9\)
- Answer b
-
\(23\)
Just as we saw with multiplication, when we divide a number by \(1\), the result is the same number. What happens when we divide a number by \(−1\)? Let’s divide a positive number and then a negative number by \(−1\) to see what we get.
| 8 ÷ (−1) | −9 ÷ (−1) |
| −8 | 9 |
| −8 is the opposite of 8 | 9 is the opposite of −9 |
When we divide a number by, \(−1\) we get its opposite.
Dividing a number by \(−1\) gives its opposite.
\[a \div (-1) = -a\]
Divide each of the following:
- \(16 ÷ (−1)\)
- \(−20 ÷ (−1)\)
Solution
| The dividend, 16, is being divided by –1. | 16 ÷ (–1) |
| Dividing a number by –1 gives its opposite. | –16 |
Notice that the signs were different, so the result was negative.
| The dividend, –20, is being divided by –1. | –20 ÷ (–1) |
| Dividing a number by –1 gives its opposite. | 20 |
Notice that the signs were the same, so the quotient was positive.
Divide:
- \(6 ÷ (−1)\)
- \(−36 ÷ (−1)\)
- Answer a
-
\(-6\)
- Answer b
-
\(36\)
Divide:
- \(28 ÷ (−1)\)
- \(−52 ÷ (−1)\)
- Answer a
-
\(-28\)
- Answer b
-
\(52\)
Simplify Expressions with Integers
Now we’ll simplify expressions that use all four operations–addition, subtraction, multiplication, and division–with integers. Remember to follow the order of operations.
Simplify: \(7(−2) + 4(−7) − 6\).
Solution
We use the order of operations. Multiply first and then add and subtract from left to right.
| Multiply first. | −14 + (−28)−6 |
| Add. | −42 − 6 |
| Subtract. | −48 |
Simplify: \(8(−3) + 5(−7)−4\)
- Answer
-
\(-63\)
Simplify: \(9(−3) + 7(−8) − 1\)
- Answer
-
\(-84\)
Simplify:
- \((−2)^4\)
- \(−2^4\)
Solution
The exponent tells how many times to multiply the base.
- The exponent is \(4\) and the base is \(−2\). We raise \(−2\) to the fourth power.
| Write in expanded form. | (−2)(−2)(−2)(−2) |
| Multiply. | 4(−2)(−2) |
| Multiply. | −8(−2) |
| Multiply. | 16 |
- The exponent is \(4\) and the base is \(2\). We raise \(2\) to the fourth power and then take the opposite.
| Write in expanded form. | −(2 • 2 • 2 • 2) |
| Multiply. | −(4 • 2 • 2) |
| Multiply. | −(8 • 2) |
| Multiply. | −16 |
Simplify:
- \((−3)^4\)
- \(−3^4\)
- Answer a
-
\(81\)
- Answer b
-
\(-81\)
Simplify:
- \((−7)^2\)
- \(−7^2\)
- Answer a
-
\(49\)
- Answer b
-
\(-49\)
Simplify: \(12 − 3(9 − 12)\).
Solution
According to the order of operations, we simplify inside parentheses first. Then we will multiply and finally we will subtract.
| Subtract the parentheses first. | 12 − 3(−3) |
| Multiply. | 12 − (−9) |
| Subtract. | 21 |
Simplify: \(17 − 4(8 − 11)\)
- Answer
-
\(29\)
Simplify: \(16 − 6(7 − 13)\)
- Answer
-
\(52\)
Simplify: \(8(−9) ÷ (−2)^3\).
Solution
We simplify the exponent first, then multiply and divide.
| Simplify the exponent. | 8(−9) ÷ (−8) |
| Multiply. | −72 ÷ (−8) |
| Divide. | 9 |
Simplify: \(12(−9) ÷ (−3)^3\)
- Answer
-
\(4\)
Simplify: \(18(−4) ÷ (−2)^3\)
- Answer
-
\(9\)
Simplify: \(−30 ÷ 2 + (−3)(−7)\).
Solution
First we will multiply and divide from left to right. Then we will add.
| Divide. | −15 + (−3)(−7) |
| Multiply. | −15 + 21 |
| Add. | 6 |
Simplify: \(−27 ÷ 3 + (−5)(−6)\)
- Answer
-
\(21\)
Simplify: \(−32 ÷ 4 + (−2)(−7)\)
- Answer
-
\(6\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


