3.3: Add Integers (Part 1)
- Page ID
- 4985
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Model addition of integers
- Simplify expressions with integers
- Evaluate variable expressions with integers
- Translate word phrases to algebraic expressions
- Add integers in applications
Before you get started, take this readiness quiz.
- Evaluate \(x + 8\) when \(x = 6\). If you missed this problem, review Example 2.2.1.
- Simplify: \(8 + 2(5 + 1)\). If you missed this problem, review Example 2.1.8.
- Translate the sum of \(3\) and negative \(7\) into an algebraic expression. If you missed this problem, review Table 2.2.3.
Model Addition of Integers
Now that we have located positive and negative numbers on the number line, it is time to discuss arithmetic operations with integers.
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more difficult. This difficulty relates to the way the brain learns.
The brain learns best by working with objects in the real world and then generalizing to abstract concepts. Toddlers learn quickly that if they have two cookies and their older brother steals one, they have only one left. This is a concrete example of \(2 − 1\). Children learn their basic addition and subtraction facts from experiences in their everyday lives. Eventually, they know the number facts without relying on cookies.
Addition and subtraction of negative numbers have fewer real world examples that are meaningful to us. Math teachers have several different approaches, such as number lines, banking, temperatures, and so on, to make these concepts real.
We will model addition and subtraction of negatives with two color counters. We let a blue counter represent a positive and a red counter will represent a negative.

If we have one positive and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero as summarized in Figure \(\PageIndex{1}\).
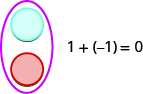
Figure \(\PageIndex{1}\): A blue counter represents +1. A red counter represents −1. Together they add to zero.
We will model four addition facts using the numbers \(5\), \(−5\) and \(3\), \(−3\).
\[5 + 3 \qquad −5 + (−3) \qquad −5 + 3 \qquad 5 + (−3) \nonumber \]
Model: \(5 + 3\).
Solution
| Interpret the expression. | 5 + 3 means the sum of 5 and 3. |
| Model the first number. Start with 5 positives. |  |
| Model the second number. Add 3 positives. |  |
| Count the total number of counters. |  |
| The sum of 5 and 3 is 8. | 5 + 3 = 8 |
Model the expression. \(2 + 4\)
- Answer
-

\(6\)
Model the expression. \(2 + 5\)
- Answer
-

\(7\)
Model: \(−5 + (−3)\).
Solution
| Interpret the expression. | −5 + (−3) means the sum of −5 and −3. |
| Model the first number. Start with 5 negatives. |  |
| Model the second number. Add 3 negatives. |  |
| Count the total number of counters. |  |
| The sum of −5 and −3 is −8. | −5 + −3 = −8 |
Model the expression. \(−2 + (−4)\)
- Answer
-

\(-6\)
Model the expression. \(−2 + (−5)\)
- Answer
-

\(-7\)
Example \(\PageIndex{1}\) and Example \(\PageIndex{2}\) are very similar. The first example adds \(5\) positives and \(3\) positives—both positives. The second example adds \(5\) negatives and \(3\) negatives—both negatives. In each case, we got a result of \(8\) -- either \(8\) positives or \(8\) negatives. When the signs are the same, the counters are all the same color. Now let’s see what happens when the signs are different.
Model: \(−5 + 3\).
Solution
| Interpret the expression. | −5 + 3 means the sum of −5 and 3. |
| Model the first number. Start with 5 negatives. |  |
| Model the second number. Add 3 positives. |  |
| Remove any neutral pairs. | 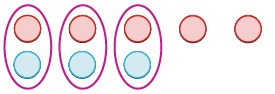 |
| Count the result. |  |
| The sum of −5 and 3 is −2. | −5 + 3 = −2 |
Notice that there were more negatives than positives, so the result is negative.
Model the expression, and then simplify: \(2 + (-4)\)
- Answer
-

\(-2\)
Model the expression, and then simplify: \(2 + (−5)\)
- Answer
-

\(-3\)
Model: \(5 + (−3)\).
Solution
| Interpret the expression. | 5 + (−3) means the sum of 5 and −3. |
| Model the first number. Start with 5 positives. |  |
| Model the second number. Add 3 negatives. |  |
| Remove any neutral pairs. | 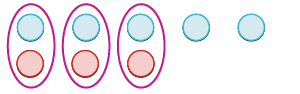 |
| Count the result. |  |
| The sum of 5 and −3 is 2. | 5 + (−3) = 2 |
Model the expression, and then simplify: \((−2) + 4\)
- Answer
-
\(2\)
Model the expression: \((−2) + 5\)
- Answer
-

\(3\)
Model each addition.
- \(4 + 2\)
- \(−3 + 6\)
- \(4 + (−5)\)
- \(-2 + (−3)\)
Solution
- \(4 + 2\)
| Start with 4 positives. |  |
| Add two positives. |  |
| How many do you have? 6. | 4 + 2 = 6 |
- \(−3 + 6\)
| Start with 3 negatives. |  |
| Add 6 positives. | 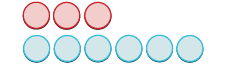 |
| Remove neutral pairs. | 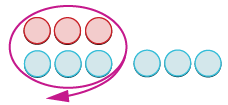 |
| How many are left? |  |
| 3. | −3 + 6 = 3 |
- \(4 + (−5)\)
| Start with 4 positives. |  |
| Add 5 negatives. | 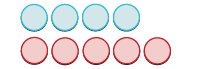 |
| Remove neutral pairs. | 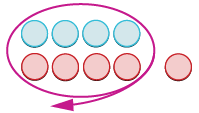 |
| How many are left? |  |
| −1. | 4 + (−5) = −1 |
- \(−2 + (−3)\)
| Start with 2 negatives. |  |
| Add 3 negatives. |  |
| How many do you have? −5. | −2 + (−3) = −5 |
Model each addition.
- \(3 + 4\)
- \(−1 + 4\)
- \(4 + (−6)\)
- \(−2 + (−2)\)
- Answer a
-

- Answer b
-

- Answer c
-

- Answer d
-

Model each addition.
- \(5 + 1\)
- \(−3 + 7\)
- \(2 + (−8)\)
- \(−3 + (−4)\)
- Answer a
-

- Answer b
-

- Answer c
-

- Answer d
-

Simplify Expressions with Integers
Now that you have modeled adding small positive and negative integers, you can visualize the model in your mind to simplify expressions with any integers.
For example, if you want to add \(37 + (−53)\), you don’t have to count out \(37\) blue counters and \(53\) red counters.
Picture \(37\) blue counters with \(53\) red counters lined up underneath. Since there would be more negative counters than positive counters, the sum would be negative. Because \(53−37 = 16\), there are \(16\) more negative counters.
\[37 + (−53) = −16 \nonumber \]
Let’s try another one. We’ll add \(−74 + (−27)\). Imagine \(74\) red counters and \(27\) more red counters, so we have \(101\) red counters all together. This means the sum is \(−101\).
\[−74 + (−27) = −101 \nonumber \]
Look again at the results of Example \(\PageIndex{1}\) - Example \(\PageIndex{2}\).
| 5 + 3 | −5 + (−3) |
|---|---|
| both positive, sum positive | both negative, sum negative |
| When the signs are the same, the counters would be all the same color, so add them. | |
| −5 + 3 | 5 + (−3) |
| different signs, more negatives | different signs, more positives |
| sum negative | sum positive |
| When the signs are different, some counters would make neutral pairs; subtract to see how many are left. | |
Simplify:
- \(19 + (−47)\)
- \(−32 + 40\)
Solution
- Since the signs are different, we subtract \(19\) from \(47\). The answer will be negative because there are more negatives than positives. \(19 + (−47)=−28\)
- The signs are different so we subtract \(32\) from \(40\). The answer will be positive because there are more positives than negatives \(−32 + 40=8\)
Simplify each expression:
- \(15 + (−32)\)
- \(−19 + 76\)
- Answer a
-
\(-17\)
- Answer b
-
\(57\)
Simplify each expression:
- \(−55 + 9\)
- \(43 + (−17)\)
- Answer a
-
\(-46\)
- Answer b
-
\(26\)
Simplify: \(−14 + (−36)\).
Solution
Since the signs are the same, we add. The answer will be negative because there are only negatives.
\[−14 + (−36)=−50 \nonumber \]
Simplify the expression: \(−31 + (−19)\)
- Answer
-
\(-50\)
Simplify the expression: \(−42 + (−28)\)
- Answer
-
\(-70\)
The techniques we have used up to now extend to more complicated expressions. Remember to follow the order of operations.
Simplify: \(−5 + 3(−2 + 7)\).
Solution
| Simplify inside the parentheses. | −5 + 3(5) |
| Multiply. | −5 + 15 |
| Add left to right. | 10 |
Simplify the expression: \(−2 + 5(−4 + 7)\)
- Answer
-
\(13\)
Simplify the expression: \(−4 + 2(−3 + 5)\)
- Answer
-
\(0\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


