1.3: Linear Functions

As you hop into a taxicab in Allentown, the meter will immediately read $3.30; this is the “drop” charge made when the taximeter is activated. After that initial fee, the taximeter will add $2.40 for each mile the taxi drives. In this scenario, the total taxi fare depends upon the number of miles ridden in the taxi, and we can ask whether it is possible to model this type of scenario with a function. Using descriptive variables, we choose \(m\) for miles and \(C\) for Cost in dollars as a function of miles: \(C(m)\).

We know for certain that \(C(0)=3.30\), since the $3.30 drop charge is assessed regardless of how many miles are driven. Since $2.40 is added for each mile driven, we could write that if \(m\) miles are driven, \(C(m)=3.30+2.40m\) because we start with a $3.30 drop fee and then for each mile increase we add $2.40.

It is good to verify that the units make sense in this equation. The $3.30 drop charge is measured in dollars; the $2.40 charge is measured in dollars per mile. So \[C(m)=3.30\text{ dollars}+\left(2.40\frac{\text{dollars}}{\text{mile}}\right) (m\text{ miles})\nonumber \] When dollars per mile are multiplied by a number of miles, the result is a number of dollars, matching the units on the 3.30, and matching the desired units for the \(C\) function.

Notice this equation \(C(m)=3.30+2.40m\) consisted of two quantities. The first is the fixed $3.30 charge which does not change based on the value of the input. The second is the $2.40 dollars per mile value, which is a rate of change. In the equation this rate of change is multiplied by the input value.

Looking at this same problem in table format we can also see the cost changes by $2.40 for every 1 mile increase:

\(m\)	0	1	2	3
\(C(m)\)	3.30	5.70	8.10	10.50

It is important here to note that in this equation, the rate of change is constant; over any interval, the rate of change is the same.

Graphing this equation, \(C(m)=3.30+2.40m\) we see the shape is a line, which is how these functions get their name: linear functions.

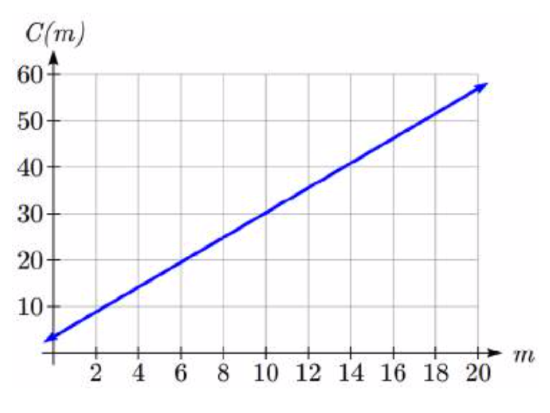
When the number of miles is zero the cost is $3.30, giving the point (0, 3.30) on the graph. This is the vertical or \(C(m)\) intercept. The graph is increasing in a straight line from left to right because for each mile the cost goes up by $2.40; this rate remains consistent.

Linear Function

A linear function is a function whose graph produces a line. Linear functions can always be written in the form \[f(x)=b+mx\nonumber \] or \[f(x)=mx+b\nonumber \] where \(b\) is the initial or starting value of the function (with input \(x = 0\)), and \(m\) is the constant rate of change of the function.

This form of a line is called slope-intercept form of a line.

Many people like to write linear functions in the form \(f(x)=b+mx\) because it corresponds to the way we tend to speak: "The output starts at \(b\) and increases at a rate of \(m\)."

For this reason alone we will use the \(f(x)=b+mx\) form for many of the examples, but remember they are equivalent and can be written correctly both ways. [While this is the book's convention, in class and in the videos I will likely use \(f(x)=mx+b\).]

Slope and Increasing/Decreasing

\(m\) is the constant rate of change of the function (also called slope). The slope determines if the function is an increasing function or a decreasing function.

• \(f(x)=b+mx\) is an increasing function if \(m\gt 0\).
• \(f(x)=b+mx\) is a decreasing function if \(m\lt 0\).

If \(m=0\), the rate of change is 0, and the function \(f(x)=b+0x=b\) is just a horizontal line passing through the point (0, b), neither increasing nor decreasing.

Example \(\PageIndex{1}\)

Marcus currently owns 200 songs in his iTunes collection. Every month, he adds 15 new songs. Write a formula for the number of songs, \(N\), in his iTunes collection as a function of the number of months, \(m\). How many songs will he own in a year?

Solution

The initial value for this function is 200, since he currently owns 200 songs, so \(N(0)=200\). The number of songs increases by 15 songs per month, so the rate of change is 15 songs per month. With this information, we can write the formula:\[N(m)=200+15m.\nonumber \]

\(N(m)\) is an increasing linear function.

With this formula we can predict how many songs he will have in 1 year (12 months): \[N(12)=200+15(12)=200+180=380.\nonumber \] Marcus will have 380 songs in 12 months.

Calculating Rate of Change

Given two values for the input, \( x_1 \) and \( x_2 \), and two corresponding values for the output, \( y_1 \) and \( y_2 \), or a set of points, \( (x_1,y_1) \) and \( (x_2,y_2) \), if we wish to find a linear function that contains both points we can calculate the rate of change, \(m\):\[m=\dfrac{\text{change in output}}{\text{change in input}}=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}.\nonumber \]

Rate of change of a linear function is also called the slope of the line.

Note in function notation, \(y_1=f(x_1)\) and \(y_2=f(x_2)\), so we could equivalently write \[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}.\nonumber \]

Example \(\PageIndex{2}\)

The population of a city increased from 23,400 to 27,800 between 2002 and 2006. Find the rate of change of the population during this time span.

Solution

The rate of change will relate the change in population to the change in time. The population increased by 27800-23400=4400 people over the 4 year time interval. To find the rate of change, the number of people per year the population changed by: \[\dfrac{4400 \text{ people}}{4\text{ years}}=1100\dfrac{\text{people}}{\text{year}}=1100 \text{ people per year}.\nonumber \]

Notice that we knew the population was increasing, so we would expect our value for \(m\) to be positive. This is a quick way to check to see if your value is reasonable.

Example \(\PageIndex{3}\)

The pressure, \(P\), in pounds per square inch (PSI) on a diver depends upon their depth below the water surface, \(d\), in feet, following the equation \(P(d)=14.696+0.43d\). Interpret the components of this function.

Solution

The rate of change, or slope, 0.434 would have units \(\dfrac{\text{output}}{\text{input}}=\dfrac{\text{pressure}}{\text{depth}}=\dfrac{\text{PSI}}{\text{ft}}\). This tells us the pressure on the diver increases by 0.434 PSI for each foot their depth increases.

The initial value, 14.696, will have the same units as the output, so this tells us that at a depth of 0 feet, the pressure on the diver will be 14.696 PSI.

We can now find the rate of change given two input-output pairs, and could write an equation for a linear function if we had the rate of change and initial value. If we have two input-output pairs and they do not include the initial value of the function, then we will have to solve for it.

Example \(\PageIndex{4}\)

Write an equation for the linear function graphed below.

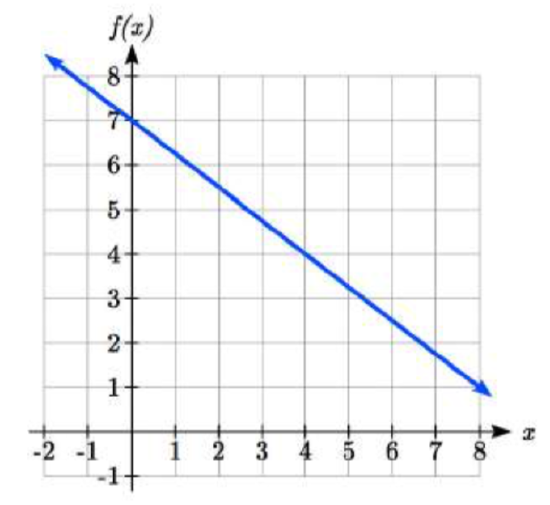
Solution

Looking at the graph, we might notice that it passes through the points (0, 7) and (4, 4). From the first value, we know the initial value of the function is \(b = 7\), so in this case we will only need to calculate the rate of change: \[m=\dfrac{4-7}{4-0}=\dfrac{-3}{4}\nonumber \]

This allows us to write the equation: \[f(x)=7-\frac{3}{4}x\nonumber \]

Example \(\PageIndex{5}\)

If \(f(x)\) is a linear function, \(f(3)=-2\), and \(f(8)=1\), find an equation for the function.

Solution

In Example \(\PageIndex{3}\), we computed the rate of change to be \(m=\frac{3}{5}\). In this case, we do not know the initial value \(f(0)\), so we will have to solve for it. Using the rate of change, we know the equation will have the form \(f(x)=b+\frac{3}{5}x\). Since we know the value of the function when \(x = 3\), we can evaluate the function at 3: \(f(x)=b+\frac{3}{5}(3)\).

Since we know that \(f(3)=-2\), we can substitute on the left side: \(-2=b+\frac{3}{5}(3)\).

This leaves us with an equation we can solve for the initial value: \(b=-2-\frac{9}{5}=-\frac{19}{5}\).

Combining this with the value for the rate of change, we can now write a formula for this function:\[f(x)=-\frac{19}{5}+\frac{3}{5}x.\nonumber \]

As an alternative to the approach used above to find the initial value, b, we can use the point-slope form of a line instead.

Point-Slope Equation of a Line

An equation for the line passing through the point \((x_1, y_1)\) with slope \(m\) can be written as \[y-y_1=m(x-x_1)\nonumber \]

This is called the point-slope form of a line. It is a little easier to write if you know a point and the slope, but requires a bit of work to rewrite into slope-intercept form, and requires memorizing another formula.

Example \(\PageIndex{6}\)

Working as an insurance salesperson, Ilya earns a base salary and a commission on each new policy, so Ilya’s weekly income, \(I\), depends on the number of new policies, n, he sells during the week. Last week he sold 3 new policies, and earned $760 for the week. The week before, he sold 5 new policies, and earned $920. Find an equation for \(I(n)\), and interpret the meaning of the components of the equation.

Solution

The given information gives us two input-output pairs: (3,760) and (5,920). We start by finding the rate of change: \[m=\dfrac{920-760}{5-3}=\dfrac{160}{2}=80.\nonumber \]

Keeping track of units can help us interpret this quantity. Income increased by $160 when the number of policies increased by 2, so the rate of change is $80 per policy; Ilya earns a commission of $80 for each policy sold during the week.

We can now write the equation using the point-slope form of the line, using the slope we just found and the point (3,760): \[I-760= 80(n-3)\nonumber \]

If we wanted this in function form (slope intercept form), we could rewrite the equation into that form: \[\begin{align*} I-760 & = 80(n-3)\\ I-760 & = 80n-240\\ I(n) & = 520+80n \end{align*}\]

This form allows us to see the starting value for the function: 520. This is Ilya’s income when \(n = 0\), which means no new policies are sold. We can interpret this as Ilya’s base salary for the week, which does not depend upon the number of policies sold.

Our final interpretation is: Ilya’s base salary is $520 per week and he earns an additional $80 commission for each policy sold each week.

Graphs of Linear Functions

Graphical Interpretation of a Linear Equation

Graphically, in the equation \(f(x)=b+mx\),

• \(b\) is the vertical intercept of the graph and tells us we can start our graph at \((0, b)\)
• and \(m\) is the slope of the line and tells us how far to rise and run to get to the next point.

Once we have at least 2 points, we can extend the graph of the line to the left and right.

Example \(\PageIndex{7}\)

Graph \(f(x)=5-\frac{2}{3}x\) using the vertical intercept and slope.

Solution

The vertical intercept of the function is (0, 5), giving us a point on the graph of the line. The slope is \(-\frac{2}{3}\). This tells us that for every 3 units the graph "runs" in the horizontal, the vertical "rise" decreases by 2 units. In graphing, we can use this by first plotting our vertical intercept on the graph, then using the slope to find a second point. From the initial value (0, 5) the slope tells us that if we move to the right 3, we will move down 2, moving us to the point (3, 3). We can continue this again to find a third point at (6, 1). Finally, extend the line to the left and right, containing these points.

Another option for graphing is to use transformations of the identity function \(f(x)=x\). In the equation \(f(x)=mx\), the \(m\) is acting as the vertical stretch of the identity function. When \(m\) is negative, there is also a vertical reflection of the graph. Looking at some examples will also help show the effect of slope on the shape of the graph:

\(f(x)=mx\) for several values of \(m\).

In \(f(x)=mx+b\), the \(b\) acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Some examples:

\(f(x)=mx+b\) for several values of \(b\).

Try it for yourself using this applet:

Example \(\PageIndex{8}\)

Match each equation with one of the lines in the graph below \[\begin{align*} f(x) & = 2x+3\\ g(x) & = 2x-3\\ h(x) & = -2x+3\\ j(x) & = \frac{1}{2}x+3 \end{align*}\]

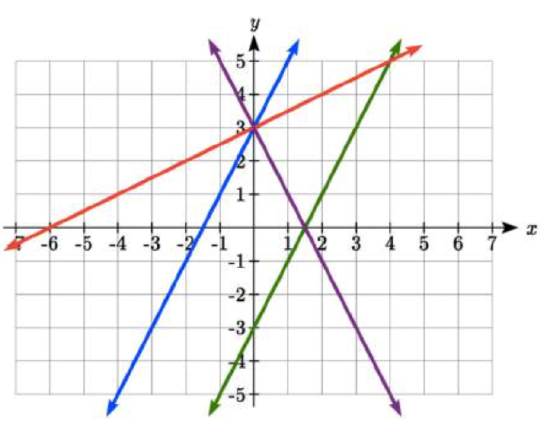
Solution

Only one graph has a vertical intercept of -3, so we can immediately match that graph with \(g(x)\). For the three graphs with a vertical intercept at 3, only one has a negative slope, so we can match that line with \(h(x)\). Of the other two, the steeper line would have a larger slope, so we can match that graph with equation \(f(x)\), and the flatter line with the equation \(j(x)\).

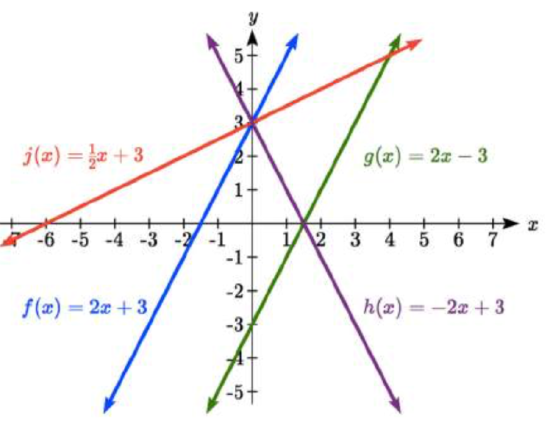
In addition to understanding the basic behavior of a linear function (increasing or decreasing, recognizing the slope and vertical intercept), it is often helpful to know the horizontal intercept of the function – where it crosses the horizontal axis.

Finding Horizontal Intercept

The horizontal intercept of the function is where the graph crosses the horizontal axis. If a function has a horizontal intercept, you can always find it by solving \(f(x)=0\).

Example \(\PageIndex{9}\)

Find the horizontal intercept of \(f(x)=-3+\frac{1}{2}x\)

Solution

Setting the function equal to zero to find what input will put us on the horizontal axis: \[\begin{align*} 0 & = -3+\frac{1}{2}x\\ 3 & = \frac{1}{2}x\\ x & = 6 \end{align*}\] Thus the graph crosses the horizontal axis at (6,0).

Intersections of Lines

The graphs of two lines will intersect if they are not parallel. They will intersect at the point that satisfies both equations. To find this point when the equations are given as functions, we can solve for an input value so that \(f(x)=g(x)\). In other words, we can set the formulas for the lines equal, and solve for the input that satisfies the equation.

Economics tells us that in a free market, the price for an item is related to the quantity that producers will supply and the quantity that consumers will demand. Increases in prices will decrease demand, while supply tends to increase with prices. Sometimes supply and demand are modeled with linear functions.

Example \(\PageIndex{10}\)

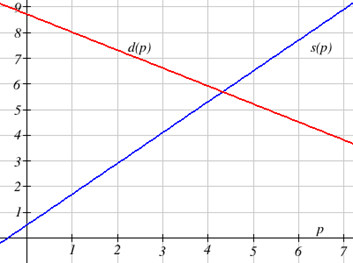
The supply, in thousands of items, for custom phone cases can be modeled by the equation \(s(p)=0.5+1.2p\) while the demand can be modeled by \(d(p)=8.7-0.7p\), where \(p\) is in dollars. Find the equilibrium price and quantity, the intersection of the supply and demand curves.

Solution

Setting \(s(p)=d(p)\), we find \[\begin{align*} 0.5+1.2p & = 8.7-0.7p\\ 1.9p & = 8.2\\ p & \approx \$4.32 \end{align*}\]

We can find the output value of the intersection point by evaluating either function at this input: \[s(4.32)=0.5+1.2(4.32)\approx 5.68\nonumber \]

These lines intersect at the point (4.32, 5.68). Looking at the graph, this result seems reasonable.

Business Applications

In business, a very common application of functions is to model cost, revenue, and profit.

Cost, Revenue, Profit

When a company produces \(q\) items, the total cost is the cost of total cost of producing those items. The total cost includes both fixed costs, which are startup costs, like equipment and buildings, and variable costs, which are costs that depend on the number of items produced, like materials and labor.

In the most simple case, Total Cost = (Fixed Costs) + (Variable Costs) \(\bf \cdot \) \(\bf q\)

Revenue is the amount of money a company brings in from sales.

In the most simple case, Revenue = (Price per item) \(\bf \cdot \) \(\bf q\)

Profit is the amount of money brings in, after expenses.

Profit = Revenue – Costs

We often talk about the break-even point. This is the level of production where Revenue equals Cost, or equivalently where Profit is zero. This is typically the minimum level of sales necessary for the company to make a profit.

Example \(\PageIndex{11}\)

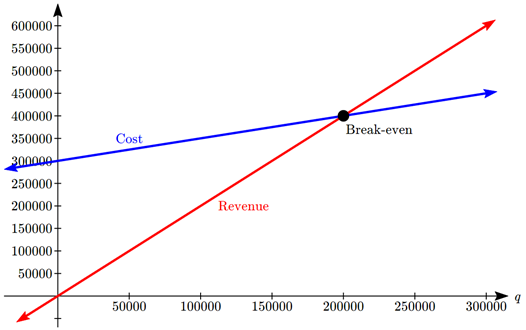
A tech startup is looking at developing and launching a new mobile app. Initial development of the app will cost $300,000, and they estimate marketing and support for each user will cost $0.50. While the app will be free, they estimate they will be able to bring in $2 per user on average from in-app purchases. How many users will the company need to break even?

Solution

We start by modeling the cost, revenue, and profit. Let \(q\) = number of users.

The fixed (initial) costs are $300,000, and the variable (per-item) costs as $0.50 per user. We can write the total cost equation:
\(TC(q) = 300,000 + 0.50q\)

The revenue will be $2 per user, so the revenue equation will be:
\(R(q) = 2q\)

We could find the break-even point by setting the total cost equal to the revenue, which is equivalent to finding the intersection of the lines.

Alternatively, we could go ahead and find a profit equation first:
\(P(q) = R(q) - TC(q) = 2q - (300,000+0.50q) = 1.5q - 300,000\)

The break even point can be found by setting the profit equal to zero: \[\begin{align*} 0 & = 1.5q - 300,000\\ q & = 200,000 \end{align*}\]

The company will have to acquire 200,000 users to break even.

In economics, there is a model for how prices are determined in a free market which states that supply and demand for a product is related to the price. The demand relationship shows the quantity of a certain product that consumers are willing to buy at a certain price. Typically the quantity demanded will decrease for an item if the price increases. The supply relationship shows the quantity of a product that suppliers are willing to produce at a certain sales price. Typically the supply demanded will increase if the price increases. Economic theory says that supply and demand will interact, and the intersection will be the equilibrium price, or market price, where the quantity supplied and demanded will be equal.

Supply and Demand

If \(p\) is the price of a product, then

\(Q_d\) is the quantity demanded

\(Q_s\) is the quantity supplied

The demand curve is a decreasing function, while the supply curve is an increasing function.

The intersection of the curves is the equilibrium price and quantity, also called the market price and quantity. This point is often notated as \(p^*\), \(Q^*\).

Later in the course you will explore supply and demand curves that are non-linear, but in this section we will focus on linear supply and demand functions.

In most economic books, you will see the supply and demand curve written with price as the input and quantity as the output, like \(Q_d = 140 - 2p\). However, supply and demand graphs are drawn with price on the vertical axis and quantity on the horizontal. We can write the equation in whichever way is more convenient for us.

Example \(\PageIndex{12}\)

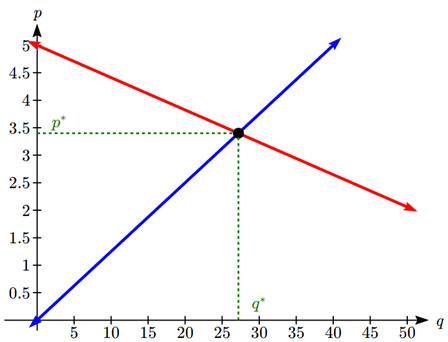
At a price of $2.50 per gallon, there is a demand in a certain town for 42.5 thousand gallons of gas and a supply of 20 thousand gallons. At a price of $3.50, there is demand for 25.5 thousand gallons and a supply of 28 thousand gallons. Assuming supply and demand are linear, find the equilibrium price and quantity.

Solution

We start by finding a linear equation for both supply and demand. We will use price, \(p\) in dollars, as the output and quantity, \(q\) in thousands of gallons, as the input.

For supply, we have the points (20, 2.50) and (28, 3.50).

Finding the slope: \(m = \dfrac{3.50-2.50}{28-20} = \frac{1}{8}\)

We know the equation will look like \(p = \frac{1}{8}q+b\), so substituting in (20, 2.50) \[\begin{align*} 2.5 & = \frac{1}{8}(20) +b \\ 2.5 & = 2.5 +b \\ q & = 0 \end{align*}\]

The supply equation is: \(p = \frac{1}{8}q\)

For demand, we have the points (42.5, 2.50) and (25.5, 3.50). Using a similar approach, we can find the demand equation is: \(p = -\frac{1}{17}q+5\)

To find the equilibrium, we set the supply equal to the demand:
\(\frac{1}{8}q = -\frac{1}{17}q+5\)

Multiplying through by 8(17) = 136 to clear the fractions,
\(136\left(\frac{1}{8}q\right) = 136\left(-\frac{1}{17}q+5\right)\)
\(17q = -8q+680\)

Now we solve for \(q\)
\(25q = 680\)
\(q = 27.2\)

To find the equilibrium price, we can substitute that value back into either equation:
\(p = \frac{1}{8}(27.2) = 3.4\)

The equilibrium quantity will be 27.2 thousand gallons of gas at a price of $3.40.