2.E: The Derivative (Exercises)
- Page ID
- 80591
2.1 Exercises
Use the graph to determine the following limits.
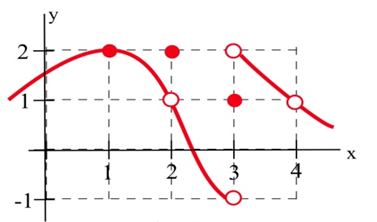
| a. \(\lim_{x \to 1} f(x)\) | b. \(\lim_{x \to 2} f(x)\) |
| c. \(\lim_{x \to 3} f(x)\) | d. \(\lim_{x \to 4} f(x)\) |
Use the graph to determine the following limits.
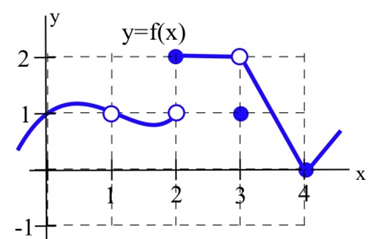
| a. \(\lim_{x \to 1} f(x)\) | b. \(\lim_{x \to 2} f(x)\) |
| c. \(\lim_{x \to 3} f(x)\) | d. \(\lim_{x \to 4} f(x)\) |
Evaluate
| a. \(\lim_{x \to 1} \frac{x^2+3x+3}{x-2}\) | b. \(\lim_{x \to 2} \frac{x^2+3x+3}{x-2}\) |
Evaluate
| a. \(\lim_{x \to 0} \frac{x+7}{x^2+9x+14}\) | b. \(\lim_{x \to 3} \frac{x+7}{x^2+9x+14}\) |
| c. \(\lim_{x \to 4} \frac{x+7}{x^2+9x+14}\) | d. \(\lim_{x \to 7} \frac{x+7}{x^2+9x+14}\) |
At which points is the function shown discontinuous?
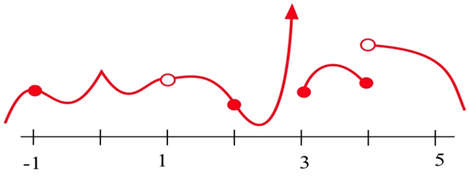
At which points is the function shown discontinuous?
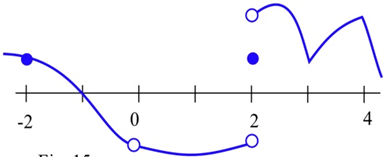
Find at least one point at which each function is not continuous and state which of the 3 conditions in the definition of continuity is violated at that point
| a. \(\frac{x+5}{x-3}\) | b. \(\frac{x^2+x-6}{x-2}\) | c. \(\frac{x}{x}\) |
| d. \(\frac{\pi}{x^2-6x+9}\) | e. \(\ln (x^2)\) |
2.2 Exercises
What is the slope of the line through (3,9) and \((x, y)\) for \(y = x^2\) and \(x = 2.97\)? \(x = 3.001\)? \(x = 3+h\)? What happens to this last slope when \(h\) is very small (close to 0)? Sketch the graph of \(y = x^2\) for \(x\) near 3.
What is the slope of the line through (–2,4) and \((x, y)\) for \(y = x^2\) and \(x = –1.98\)? \(x = –2.03\)? \(x = –2+h\)? What happens to this last slope when \(h \) is very small (close to 0)? Sketch the graph of \(y = x^2\) for \(x\) near –2.
What is the slope of the line through (2,4) and \((x, y)\) for \(y = x^2 + x – 2\) and \(x = 1.99\)?
\(x = 2.004\)? \(x = 2+h\)? What happens to this last slope when \(h\) is very small? Sketch the graph of \(y = x^2 + x – 2\) for \(x\) near 2.
What is the slope of the line through (–1,–2) and \((x, y)\) for \(y = x^2 +x – 2\) and \(x = –.98\)?
\(x = –1.03\)? \(x = –1+h\)? What happens to this last slope when \(h\) is very small? Sketch the graph of \(y = x^2 + x – 2\) for \(x\) near –1.
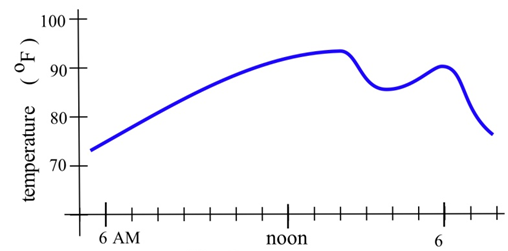
The graph to the right shows the temperature during a day in Ames.
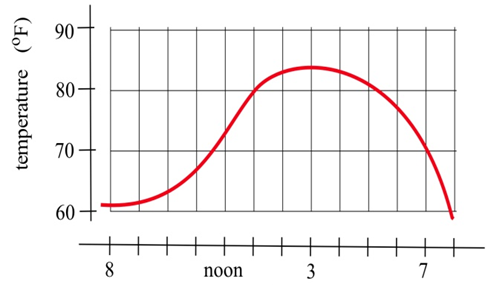
(a) What was the average change in temperature from 9 am to 1 pm?
(b) Estimate how fast the temperature was rising at 10 am and at 7 pm?
The graph shows the distance of a car from a measuring position located on the edge of a straight road.
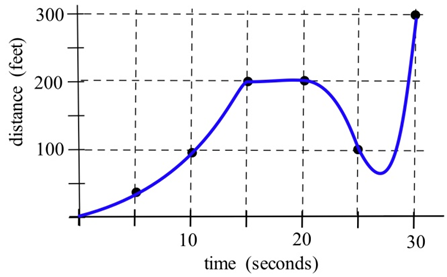
(a) What was the average velocity of the car from \(t = 0\) to \(t = 30\) seconds?
(b) What was the average velocity of the car from \(t = 10\) to \(t = 30\) seconds?
(c) About how fast was the car traveling at \(t = 10\) seconds? at \(t = 20\) s? at \(t = 30\) s?
(d) What does the horizontal part of the graph between \(t = 15\) and \(t = 20\) seconds mean?
(e) What does the negative velocity at \(t = 25\) represent?
The graph shows the distance of a car from a measuring position located on the edge of a straight road.
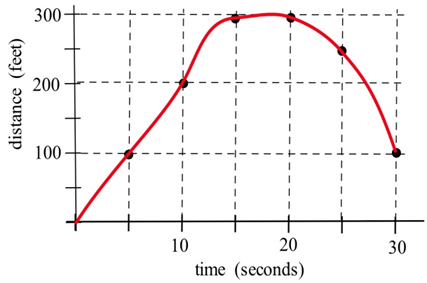
(a) What was the average velocity of the car from \(t = 0\) to \(t = 20\) seconds?
(b) What was the average velocity from \(t = 10\) to \(t = 30\) seconds?
(c) About how fast was the car traveling at \(t = 10\) seconds? at \(t = 20\) s? at \(t = 30\) s?
The graph shows the composite developmental skill level of chessmasters at different ages as determined by their performance against other chessmasters. (From "Rating Systems for Human Abilities", by W.H. Batchelder and R.S. Simpson, 1988. UMAP Module 698.)
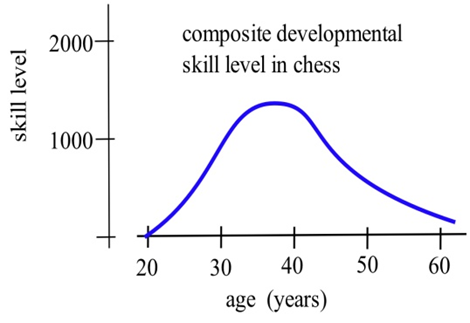
(a) At what age is the "typical" chessmaster playing the best chess?
(b) At approximately what age is the chessmaster's skill level increasing most rapidly?
(c) Describe the development of the "typical" chessmaster's skill in words.
(d) Sketch graphs which you think would reasonably describe the performance levels versus age for an athlete, a classical pianist, a rock singer, a mathematician, and a professional in your major field.
Use the function in the graph to fill in the table and then graph \(m(x)\).
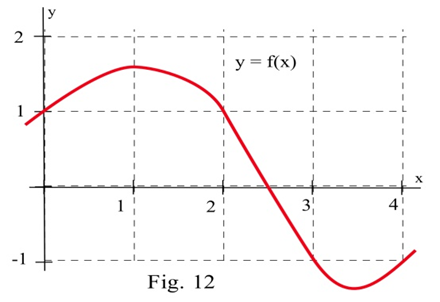
| \(x\) | \(y = f(x)\) | \(m(x) = \) the estimated slope of the tangent line to \(y=f(x)\) at the point \((x,y)\) |
| 0 | ||
| 0.5 | ||
| 1.0 | ||
| 1.5 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 | ||
| 3.5 | ||
| 4.0 |
Use the function in the graph to fill in the table and then graph \(m(x)\).
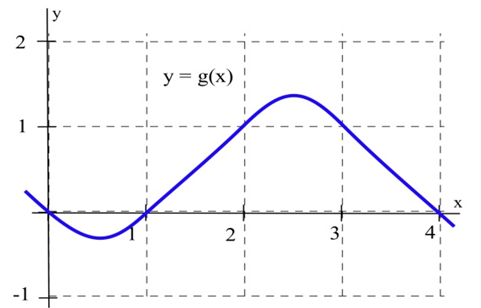
| \(x\) | \(y = g(x)\) | \(m(x) = \) the estimated slope of the tangent line to \(y=g(x)\) at the point \((x,y)\) |
| 0 | ||
| 0.5 | ||
| 1.0 | ||
| 1.5 | ||
| 2.0 | ||
| 2.5 | ||
| 3.0 | ||
| 3.5 | ||
| 4.0 |
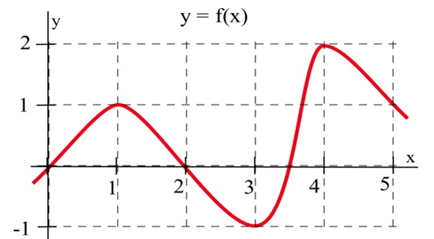
(a) At what values of \(x\) does the graph of \(f\) in the graph have a horizontal tangent line?
(b) At what value(s) of \(x\) is the value of \(f\) the largest? smallest?
(c) Sketch the graph of \(m(x)\) = the slope of the line tangent to the graph of \(f\) at the point \((x,y)\)
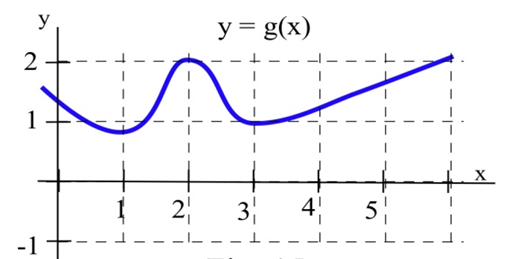
(a) At what values of \(x\) does the graph of \(g\) have a horizontal tangent line?
(b) At what value(s) of \(x\) is the value of \(g\) the largest? smallest?
(c) Sketch the graph of \(m(x) =\) the slope of the line tangent to the graph of \(g\) at the point \((x,y)\).
Match the situation descriptions with the corresponding time–velocity graph.
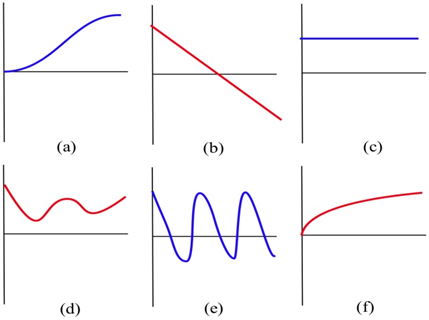
(a) A car quickly leaving from a stop sign.
(b) A car sedately leaving from a stop sign.
(c) A student bouncing on a trampoline.
(d) A ball thrown straight up.
(e) A student confidently striding across campus to take a calculus test.
(f) An unprepared student walking across campus to take a calculus test.
For each function \(f(x)\) in problems 14 – 19, perform steps (a) – (d):
(a) calculate \(m_{\sec} = \frac{f(x+h)-f(x)}{h}\) and simplify
(b) determine \(m_{\tan} = \lim_{h \to 0} m_{\sec}\)
(c) evaluate \(m_{\tan} \) at \(x = 2\),
(d) find the equation of the line tangent to the graph of \(f\) at \((2, f(2) )\)
| 14. \(f(x) = 3x – 7\) | 15. \(f(x) = 2 – 7x\) | 16. \(f(x) = ax + b\) where \(a\) and \(b\) are constants |
| 17. \(f(x) = x^2 + 3x\) | 18. \(f(x) = 8 – 3x^2\) | 19. \(f(x) = ax^2 + bx + c\) where \(a\), \(b\) and \(c\) are constants |
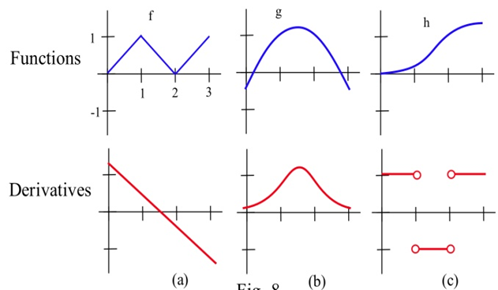
Match the graphs of the three functions below with the graphs of their derivatives.
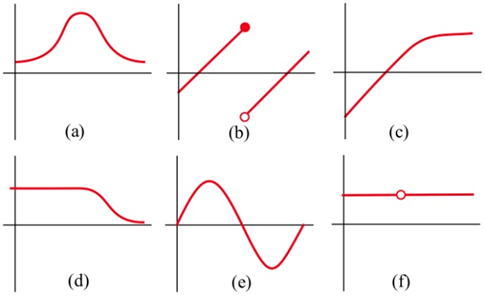
Below are six graphs, three of which are derivatives of the other three. Match the functions with their derivatives.
The graph below shows the temperature during a summer day in Chicago. Sketch the graph of the rate at which the temperature is changing. (This is just the graph of the slopes of the lines which are tangent to the temperature graph.)
Fill in the table with the appropriate units for \(f '(x)\).
|
units for \(x\) |
units for \(f(x)\) |
units for \(f '(x)\) |
|
hours |
miles |
|
|
people |
automobiles |
|
|
dollars |
pancakes |
|
|
days |
trout |
|
|
seconds |
miles per second |
|
|
seconds |
gallons |
|
|
study hours |
test points |
If \(C(x)\) is the total cost, in millions, of producing \(x\) thousand items, interpret \(C'(4) = 2\).
Suppose \(P(t)\) is the number of individuals infected by a disease \(t\) days after it was first detected. Interpret \(P'(50) = -200\).
2.3 Exercises
Fill in the values in the table for \(\frac{d}{dx} (3(f(x))\), \(\frac{d}{dx}(2f(x)+g(x))\), and \(\frac{d}{dx}(3(g(x)-f(x))\).
| \(x\) | \(f(x)\) | \(f'(x)\) | \(g(x)\) | \(g'(x)\) | \(\frac{d}{dx} (3(f(x))\) | \(\frac{d}{dx}(2f(x)+g(x))\) | \(\frac{d}{dx}(3(g(x)-f(x))\) |
| 0 | 3 | -2 | -4 | 3 | |||
| 1 | 2 | -1 | 1 | 0 | |||
| 2 | 4 | 2 | 3 | 1 |
Find
(a) \(D( x^{12} )\)
(b) \(\frac{d}{dx} (\sqrt[7]{x})\)
(c) \(D(\frac{1}{x^3})\)
(d) \(\frac{d x^e}{dx}\)
Find
(a) \(D( x^{9} )\)
(b) \(\frac{d x^{2/3}}{dx}\)
(c) \(D(\frac{1}{x^4})\)
(d) \(D(x^{\pi})\)
In problems 4 – 8, (a) calculate \(f '(1)\) and (b) determine when \(f '(x) = 0\).
| 4. \(f(x) = x^2 – 5x + 13\) |
| 5. \(f(x) = 5x^2 – 40x + 73\) |
| 6. \(f(x) = x^3 + 9x^2 + 6\) |
| 7. \(f(x) = x^3 + 3x^2 + 3x – 1\) |
| 8. \(f(x) = x^3 + 2x^2 + 2x – 1\) |
Where do \(f(x) = x^2 – 10x + 3\) and \(g(x) = x^3 – 12x\) have horizontal tangent lines?
It takes \(T(x) = x^2\) hours to weave \(x\) small rugs. What is the marginal production time to weave a rug? (Be sure to include the units with your answer.)
It costs \(C(x) = \sqrt{x}\) dollars to produce x golf balls. What is the marginal production cost to make a golf ball? What is the marginal production cost when \(x = 25\)? when \(x= 100\)? (Include units.)
An arrow shot straight up from ground level with an initial velocity of 128 feet per second will be at height \(h(x) = –16x^2 + 128x\) feet at \(x\) seconds.
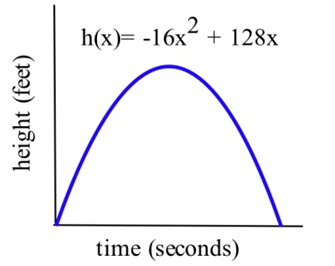
(a) Determine the velocity of the arrow when \(x =\) 0, 1 and 2 seconds.
(b) What is the velocity of the arrow, \(v(x)\), at any time \(x\)?
(c) At what time \(x\) will the velocity of the arrow be 0?
(d) What is the greatest height the arrow reaches?
(e) How long will the arrow be aloft?
(f) Use the answer for the velocity in part (b) to determine the acceleration, \(a(x) = v '(x)\), at any time \(x\).
If an arrow is shot straight up from ground level on the moon with an initial velocity of 128 feet per second, its height will be \(h(x) = –2.65x^2 + 128x\) feet at \(x\) seconds. Do parts (a) – (e) of problem 40 using this new equation for \(h\).
\(f(x) = x^3 + A x^2 + B x + C\) with constants \(A\), \(B\) and \(C\). Can you find conditions on the constants \(A\), \(B\) and \(C\) which will guarantee that the graph of \(y = f(x)\) has two distinct "vertices"? (Here a "vertex" means a place where the curve changes from increasing to decreasing or from decreasing to increasing.)
2.4 Exercises
Use the values in the table to fill in the rest of the table.
| \(x\) | \(f(x)\) | \(f'(x)\) | \(g(x)\) | \(g'(x)\) | \(\frac{d}{dx} (f(x) \cdot g(x))\) | \(\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right)\) | \(\frac{d}{dx}\left(\frac{g(x)}{f(x)}\right)\) |
| 0 | 3 | -2 | -4 | 3 | |||
| 1 | 2 | -1 | 1 | 0 | |||
| 2 | 4 | 2 | 3 | 1 |
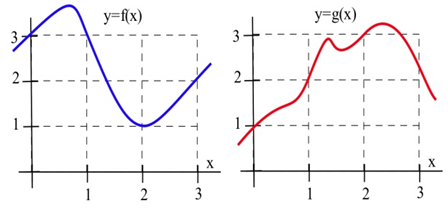
2. Use the information in the graph to plot the values of the functions \(f + g\), \(f \cdot g\) and \(f/g\) and their derivatives at \(x =\) 1, 2 and 3.
3. Use the information in the graph to plot the values of the functions \(2f\), \(f – g\) and \(g/f\) and their derivatives at \(x =\) 1, 2 and 3.
Calculate \(\frac{d}{dx} ((x-5)(3x+7))\) by (a) using the product rule and (b) expanding the product and then differentiating. Verify that both methods give the same result.
If the product of \(f\) and \(g\) is a constant \(( f(x) \cdot g(x) = k\) for all \(x\)), then how are \(\frac{\frac{d}{dx}(f(x))}{f(x)}\) and \(\frac{\frac{d}{dx}(g(x))}{g(x)}\) related?
If the quotient of \(f\) and \(g\) is a constant ( \(\frac{f(x)}{g(x)} = k\) for all \(x\)), then how are \(g \cdot f'\) and \(f \cdot g '\) related?
In problems 7 – 8, (a) calculate \(f '(1)\) and (b) determine when \(f '(x) = 0\)
| 7. \(f(x) = \frac{7x}{x^2+4}\) | 8. \(f(x) = \frac{3x^2}{2x-3}\) |
Determine \(\frac{d}{dx}(x^2 + 1)(7x - 3)\) and \(\frac{d}{dt}(\frac{3t-2}{5t+1})\).
Find (a) \(\frac{d}{dx}(x^3e^x)\) and (b) \(\frac{d}{dx}(e^x)^3\).
Find (a) \(\frac{d}{dt} (te^t)\), (b) \(d(e^x)^5\)
A manufacturer has determined that an employee with d days of production experience will be able to produce approximately \(P(d) = 3 + 15( 1 – e^{–0.2d} )\) items per day. Graph \(P(d)\).
(a) Approximately how many items will a beginning employee be able to produce each day?
(b) How many items will an experienced employee be able to produce each day?
(c) What is the marginal production rate of an employee with 5 days of experience? (What are the units of your answer, and what does this answer mean?
2.5 Exercises
The graph of \(y = f(x)\) is shown.
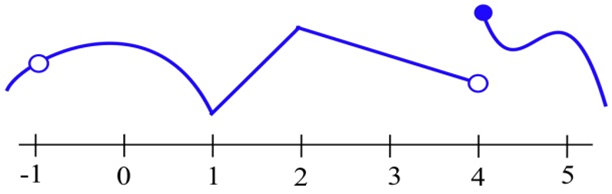
(a) At which integers is \(f\) continuous?
(b) At which integers is \(f\) differentiable?
The graph of \(y = g(x)\) is shown.
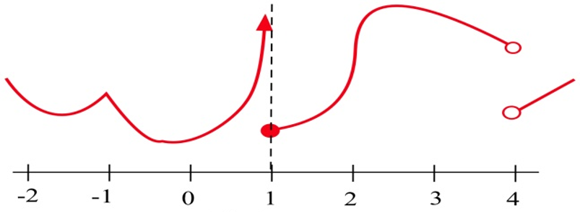
(a) At which integers is \(g\) continuous?
(b) At which integers is \(g\) differentiable?
Problems 3 and 4 refer to the values given in this table:
| \(x\) | \(f(x)\) | \(g(x)\) | \(f'(x)\) | \(g'(x)\) | \((f \circ g)(x)\) | \((f \circ g)' (x)\) |
| -2 | 2 | -1 | 1 | 1 | ||
| -1 | 1 | 2 | 0 | 2 | ||
| 0 | -2 | 1 | 2 | -1 | ||
| 1 | 0 | -2 | -1 | 2 | ||
| 2 | 1 | 0 | 1 | -1 |
3. Use the table of values to determine \(( f \circ g )(x)\) and \(( f \circ g )' (x)\) at \(x =\) 1 and 2.
4. Use the table of values to determine \(( f \circ g )(x)\) and \(( f \circ g )' (x)\) at \(x =\) –2, –1 and 0.
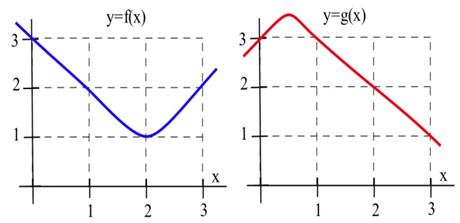
5. Use the graphs to estimate the values of \(g(x)\), \(\bf g '(x)\), \((f \circ g)(x)\), \(\mathbf{f '(} g(x) \mathbf{)}\), and \(\mathbf{( f \circ g ) '(} x \mathbf{)}\) at \(x = 1\).
6. Use the graphs to estimate the values of \(g(x)\), \(\bf g '(x)\), \((f \circ g)(x)\), \(\mathbf{f '(} g(x) \mathbf{)}\), and \(\mathbf{( f \circ g ) '(} x \mathbf{)}\) for \(x = 2\).
In problems 7 – 12, find the derivative of each function.
| 7. \(f(x) = (2x – 8)^5\) | 8. \(f(x) = (6x – x^2)^{10}\) | 9. \(f(x) = x \cdot (3x + 7)^5\) |
| 10. \(f(x) = (2x + 3)^6 \cdot (x – 2)^4\) | 11. \(f(x) = \sqrt{x^2 + 6x - 1}\) | 12. \(f(x) = \frac{x-5}{(x+3)^4}\) |
If \(f\) is a differentiable function,
(a) how are the graphs of \(y = f(x)\) and \(y = f(x) + k\) related?
(b) how are the derivatives of \(f(x)\) and \(f(x) + k\) related?
2.6 Exercises
In problems 1 and 2, each quotation is a statement about a quantity of something changing over time. Let \(f(t)\) represent the quantity at time \(t\). For each quotation, tell what \(f\) represents and whether the first and second derivatives of \(f\) are positive or negative.
1. (a) "Unemployment rose again, but the rate of increase is smaller than last month."
(b) "Our profits declined again, but at a slower rate than last month."
(c) "The population is still rising and at a faster rate than last year."
2. (a) "The child's temperature is still rising, but slower than it was a few hours ago."
(b) "The number of whales is decreasing, but at a slower rate than last year."
(c) "The number of people with the flu is rising and at a faster rate than last month."
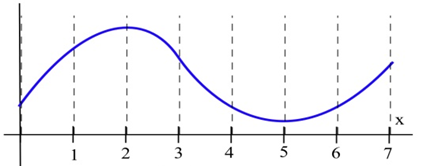
On which intervals is the function in the graph (a) concave up? (b) concave down?
On which intervals is the function in graph (a) concave up? (b) concave down?
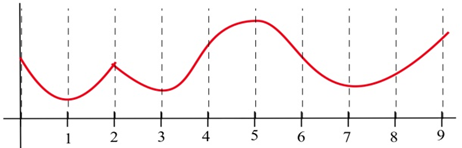
Sketch the graphs of functions which are defined and concave up everywhere and which have
(a) no roots.
(b) exactly 1 root.
(c) exactly 2 roots.
(d) exactly 3 roots.
In problems 6 – 9, a function and values of \(x\) so that \(f '(x) = 0\) are given. Use the Second Derivative Test to determine whether each point \((x, f(x))\) is a local maximum, a local minimum or neither
| 6. \(f(x) = 2x^3 – 15x^2 + 6, x = 0, 5 \). |
| 7. \(g(x) = x^3 – 3x^2 – 9x + 7, x = –1, 3 \). |
| 8. \(h(x) = x^4 – 8x^2 – 2, x = –2, 0, 2 \). |
| 9. \(f(x) = x \cdot \ln(x), x = 1/e \). |
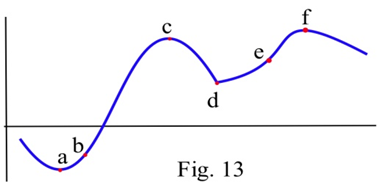
Which of the labeled points in the graph are inflection points?
Which of the labeled points in the graph are inflection points?
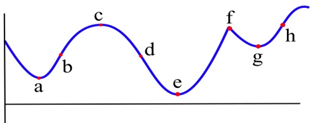
How many inflection points can a
(a) quadratic polynomial have?
(b) cubic polynomial have?
(c) polynomial of degree \(n\) have?
Fill in the table with "+", "–", or "0" for the function shown.
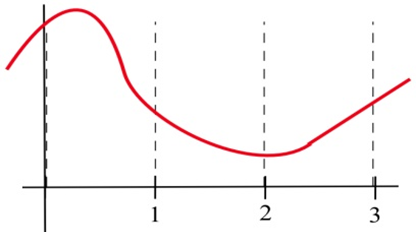
| \(x\) | \(f(x)\) | \(f'(x)\) | \(f''(x)\) |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 |
Fill in the table with "+", "–", or "0" for the function shown.
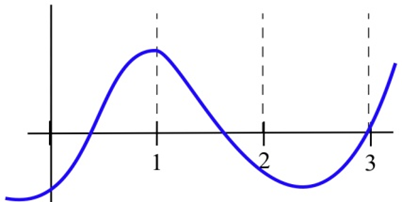
| \(x\) | \(g(x)\) | \(g'(x)\) | \(g''(x)\) |
| 0 | |||
| 1 | |||
| 2 | |||
| 3 |
In problems 15 – 21, find the derivative and second derivative of each function.
| 15. \(f(x) = 7x^2 + 5x – 3\) |
| 16. \(f(x) = (2x – 8)^5\) |
| 17. \(f(x) = (6x – x^2)^{10}\) |
| 18. \(f(x) = x \cdot (3x + 7)^5 \) |
| 19. \(f(x) = (2x^3 + 3)^6\) |
| 20. \(f(x) = \sqrt{x^2 + 6x - 1}\) |
| 21. \(f(x) = \ln (x^2+4)\) |
2.7 Exercises
Find all of the critical points of the function shown and identify them as local max, local min, or neither. Find the global max and min on the interval.
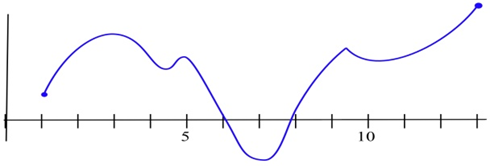
Find all of the critical points of the function shown and identify them as local max, local min, or neither. Find the global max and min on the interval.
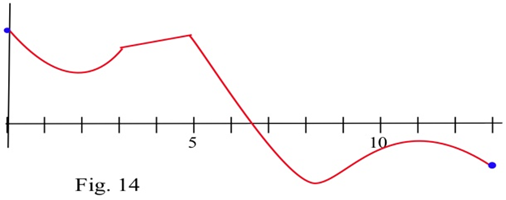
In problems 3 – 8, find all of the critical points and local maximums and minimums of each function.
| 3. \(f(x) = x^2 + 8x + 7\) | 4. \(f(x) = 2x^2 – 12x + 7\) |
| 5. \(f(x) = x^3 – 6x^2 + 5\) | 6. \(f(x) = (x – 1)^2 (x – 3)\) |
| 7. \(f(x) = \ln ( x^2 – 6x + 11 )\) | 8. \(f(x) = 2x^3 – 96x + 42\) |
In problems 9 – 16, find all critical points and global extremes of each function on the given intervals.
| 9. \(f(x) = x^2 – 6x + 5\) on the entire real number line. |
| 10. \(f(x) = 2 – x^3\) on the entire real number line. |
| 11. \(f(x) = x^3 – 3x + 5\) on the entire real number line. |
| 12. \(f(x) = x - e^x\) on the entire real number line. |
| 13. \(f(x) = x^2 – 6x + 5\) on [ –2, 5]. |
| 14. \(f(x) = 2 – x^3\) on [ –2, 1]. |
| 15. \(f(x) = x^3 – 3x + 5\) on [ –2, 1]. |
| 16. \(f(x) = x-e^x\) on [ 1, 2]. |
Suppose \(f(1) = 5\) and \(f '(1) = 0\). What can we conclude about the point (1,5) if
(a) \(f '(x) < 0\) for \(x < 1\), and \(f '(x) > 0\) for \(x > 1\)?
(b) \(f '(x) < 0\) for \(x < 1\), and \(f '(x) < 0\) for \(x > 1\)?
(c) \(f '(x) > 0\) for \(x < 1\), and \(f '(x) < 0\) for \(x > 1\)?
(d) \(f '(x) > 0\) for \(x < 1\), and \(f '(x) > 0\) for \(x > 1\)?
Define \(A(x)\) to be the area bounded between the \(x\)–axis, the graph of \(f\), and a vertical line at \(x\).
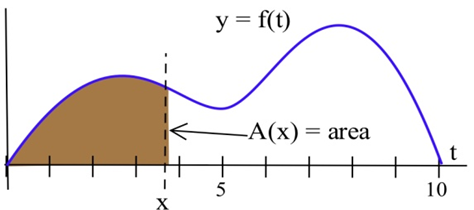
(a) At what value of \(x\) is \(A(x)\) minimum?
(b) At what value of \(x\) is \(A(x)\) maximum?
Define \(S(x)\) to be the slope of the line through the points \((0,0)\) and \(( x, f(x) )\) based on the graph of \(f\) shown.
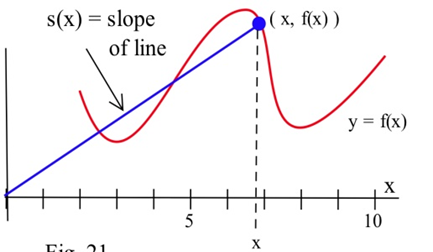
(a) At what value of \(x\) is \(S(x)\) minimum?
(b) At what value of \(x\) is \(S(x)\) maximum?
The graph of the derivative of a continuous function \(f\).
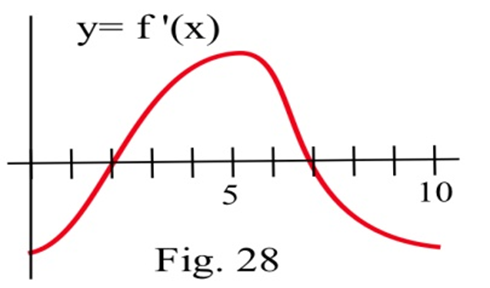
(a) List the critical numbers of \(f\).
(b) For what values of \(x\) does \(f\) have a local maximum?
(c) For what values of \(x\) does \(f\) have a local minimum?
The graph of the derivative of a continuous function \(g\).
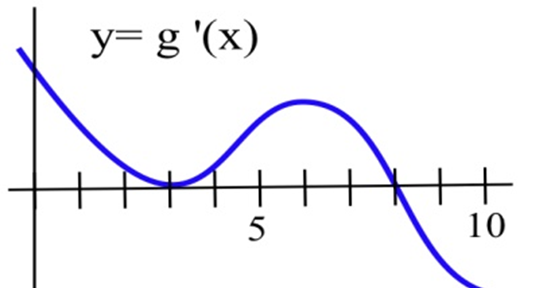
(a) List the critical numbers of \(g\).
(b) For what values of \(x\) does \(g\) have a local maximum?
(c) For what values of \(x\) does \(g\) have a local minimum?
In problems 22 – 24, a function and values of \(x\) so that \(f '(x) = 0\) are given. Use the Second Derivative Test to determine whether each point \((x, f(x))\) is a local maximum, a local minimum or neither
| 22. \(f(x) = 2x^3 – 15x^2 + 6, x = 0, 5 \). |
| 23. \(g(x) = x^3 – 3x^2 – 9x + 7, x = –1, 3\). |
| 24. \(h(x) = x^4 – 8x^2 – 2, x = –2, 0, 2 \). |
2.8 Exercises
Sketch the graph of a continuous function \(f\) so that
(a) \(f(1) = 3\), \(f '(1) = 0 \), and the point (1,3) is a local maximum of \(f\).
(b) \(f(2) = 1\), \(f '(2) = 0 \), and the point (2,1) is a local minimum of \(f\).
(c) \(f(5) = 4\), \(f '(5) = 0\), and the point (5,4) is not a local minimum or maximum of \(f\).
In problems 2–4, sketch the graph of the derivative of each function.
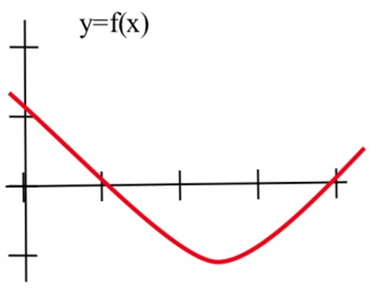
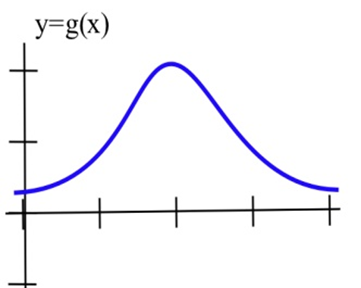
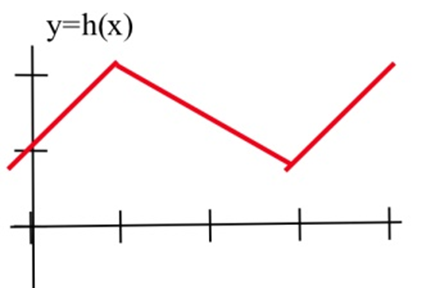
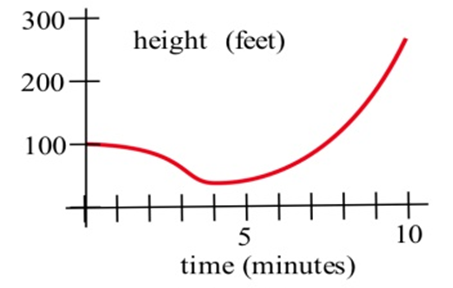
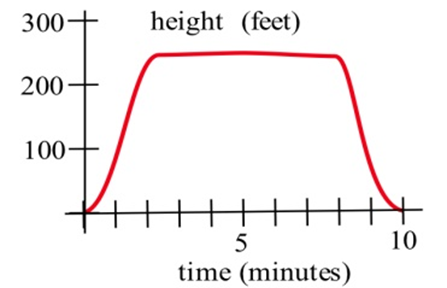
In problems 5–7, the graph of the height of a helicopter is shown. Sketch the graph of the upward velocity of the helicopter.
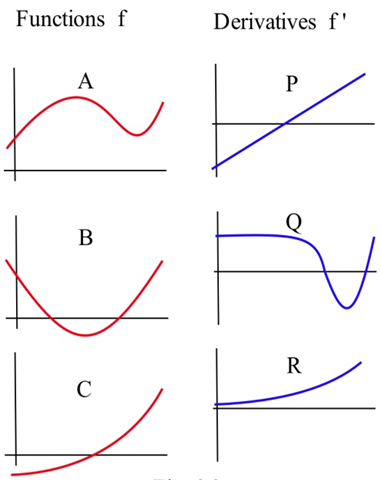
In the graphs to the right, match the graphs of the functions with those of their derivatives
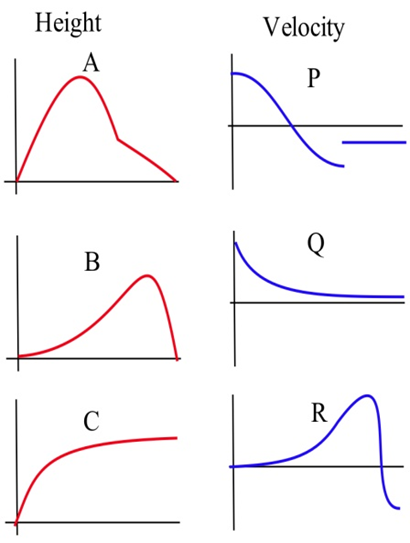
In the graphs below, match the graphs showing the heights of rockets with those showing their velocities.
In problems 10 – 14, use information from the derivatives of each function to help you graph the function. Find all local maximums and minimums of each function.
| 10. \(f(x) = x^3 – 3x^2 – 9x – 5\) | 11. \(g(x) = 2x^3 – 15x^2 + 6\) | 12. \(h(x) = x^4 – 8x^2 + 3\) |
| 13. \(r(t) = \frac{2}{t^2+1}\) | 14. \(f(x) = \frac{x^2+3}{x}\) |
2.9 Exercises
(a) You have 200 feet of fencing available to construct a rectangular pen with a fence divider down the middle (see below). What dimensions of the pen enclose the largest total area?
(b) If you need 2 dividers, what dimensions of the pen enclose the largest area?
(c) What are the dimensions in parts (a) and (b) if one edge of the pen borders on a river and does not require any fencing?
You have 120 feet of fencing to construct a pen with 4 equal sized stalls. If the pen is rectangular and shaped like the one below, what are the dimensions of the pen of largest area and what is that area?
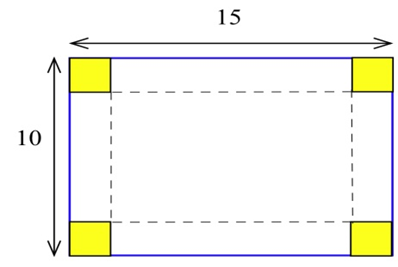
Suppose you decide to fence the rectangular garden in the corner of your yard. Then two sides of the garden are bounded by the yard fence which is already there, so you only need to use the 80 feet of fencing to enclose the other two sides. What are the dimensions of the new garden of largest area? What are the dimensions of the rectangular garden of largest area in the corner of the yard if you have \(F\) feet of new fencing available?
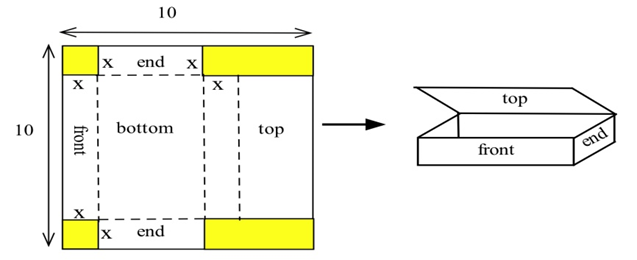
(a) You have a 10 inch by 15 inch piece of tin which you plan to form into a box (without a top) by cutting a square from each corner and folding up the sides. How much should you cut from each corner so the resulting box has the greatest volume?
(b) If the piece of tin is \(A\) inches by \(B\) inches, how much should you cut from each corner so the resulting box has the greatest volume?
You have a 10 inch by 10 inch piece of cardboard which you plan to cut and fold as shown to form a box with a top. Find the dimensions of the box which has the largest volume.
(a) You have been asked to bid on the construction of a square-bottomed box with no top which will hold 100 cubic inches of water. If the bottom and sides are made from the same material, what are the dimensions of the box which uses the least material? (Assume that no material is wasted.)
(b) Suppose the box in part (a) uses different materials for the bottom and the sides. If the bottom material costs 5¢ per square inch and the side material costs 3¢ per square inch, what are the dimensions of the least expensive box which will hold 100 cubic inches of water?
(a) Determine the dimensions of the least expensive cylindrical can which will hold 100 cubic inches if the materials cost 2¢, 5¢ and 3¢ respectively for the top, bottom and sides.
(b) How do the dimensions of the least expensive can change if the bottom material costs more than 5¢ per square inch?
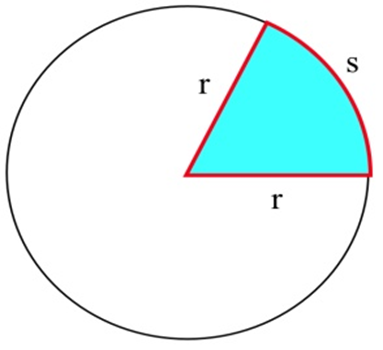
You have 100 feet of fencing to build a pen in the shape of a circular sector, the "pie slice" shown. The area of such a sector is \((rs)/2\). What value of \(r\) maximizes the enclosed area?
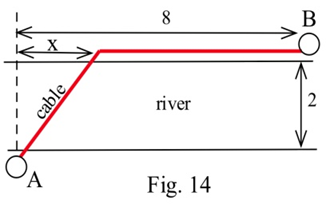
(a) You have been asked to determine the least expensive route for a telephone cable which connects Andersonville with Beantown. If it costs $5000 per mile to lay the cable on land and $8000 per mile to lay the cable across the river and the cost of the cable is negligible, find the least expensive route.
(b) What is the least expensive route if the cable costs $7000 per mile plus the cost to lay it.
You have been asked to determine where a water works should be built along a river between Chesterville and Denton to minimize the total cost of the pipe to the towns.
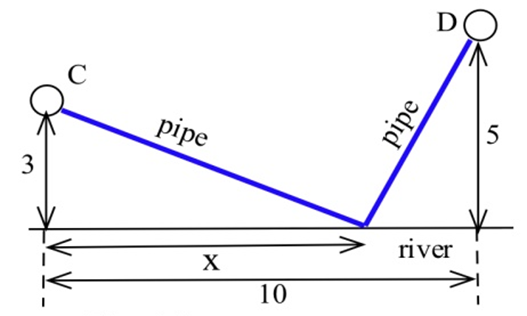
(a) Assume that the same size (and cost) pipe is used to each town. (This part can be done quickly without using calculus.)
(b) Assume that the pipe to Chesterville costs $3000 per mile and to Denton it costs $7000 per mile.
U.S. postal regulations state that the sum of the length and girth (distance around) of a package must be no more than 108 inches.
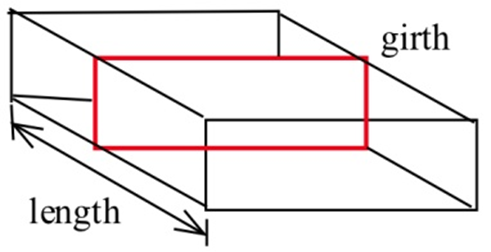
(a) Find the dimensions of the acceptable box with a square end which has the largest volume.
(b) Find the dimensions of the acceptable box which has the largest volume if its end is a rectangle twice as long as it is width.
(c) Find the dimensions of the acceptable box with a circular end which has the largest volume.
D. Simonton claims that the "productivity levels" of people in different fields can be described as a function of their "career age" \(t\) by \(p(t) = e^{–at} – e^{ –bt}\) where \(a\) and \(b\) are constants which depend on the field of work, and career age is approximately 20 less than the actual age of the individual.
(a) Based on this model, at what ages do mathematicians \((a=.03, b=.05)\), geologists \((a=.02, b=.04)\), and historians \((a=.02, b=.03)\) reach their maximum productivity?
(b) Simonton says "With a little calculus we can show that the curve \(( p(t) )\) maximizes at \(t = \frac{1}{b-a} \ln(\frac{b}{a})\)." Use calculus to show that Simonton is correct.
Note: Models of this type have uses for describing the behavior of groups, but it is dangerous and usually invalid to apply group descriptions or comparisons to individuals in the group.
(Scientific Genius, by Dean Simonton, Cambridge University Press, 1988, pp. 69 – 73)
You own a small airplane which holds a maximum of 20 passengers. It costs you $100 per flight from St. Thomas to St. Croix for gas and wages plus an additional $6 per passenger for the extra gas required by the extra weight. The charge per passenger is $30 each if 10 people charter your plane (10 is the minimum number you will fly), and this charge is reduced by $1 per passenger for each passenger over 10 who goes (that is, if 11 go they each pay $29, if 12 go they each pay $28, etc.). What number of passengers on a flight will maximize your profits?
In the planning of a coffee shop, we estimate that if there is seating for between 40 and 80 people, the daily profit will be $50 per seat. However, if the seating capacity is more than 80 places, the daily profit per seat will be decreased by $1 for each additional seat over 80. What should the seating capacity be in order to maximize the coffee shop’s total profit?
In the planning of a taco restaurant, we estimate that if there is seating for between 10 and 40 people, the daily profit will be $10 per seat. However, if the seating capacity is more than 40 places, the daily profit per seat will be decreased by $0.20 per seat. What should the seating capacity be in order to maximize the taco restaurant’s total profit?
The total cost in dollars for Alicia to make \(q\) oven mitts is given by \(C(q) = 64+1.5q+.01q^2\).
(a) What is the fixed cost?
(b) Find a function that gives the marginal cost.
(c) Find a function that gives the average cost.
(d) Find the quantity that minimizes the average cost.
(e) Confirm that the average cost and marginal cost are equal at your answer to part (d).
Shaki makes and sells backpack danglies. The total cost in dollars for Shaki to make \(q\) danglies is given by \(C(q) = 75+2q+.015q^2\). Find the quantity that minimizes Shaki’s average cost for making danglies.
2.10 Exercises
If \(g(20) = 35\) and \(g'(20)=-2\), estimate the value of \(g(22)\).
If \(g(1)=-17\) and \(g'(1)=5\), estimate the value of \(g(1.2)\).
Use the Tangent Line Approximation to estimate the cube root of 9.
Use the Tangent Line Approximation to estimate the fifth root of 30.
A rectangle has one side on the \(x\)–axis, one side on the \(y\)–axis, and a corner on the graph of \(y = x^2 + 1\).
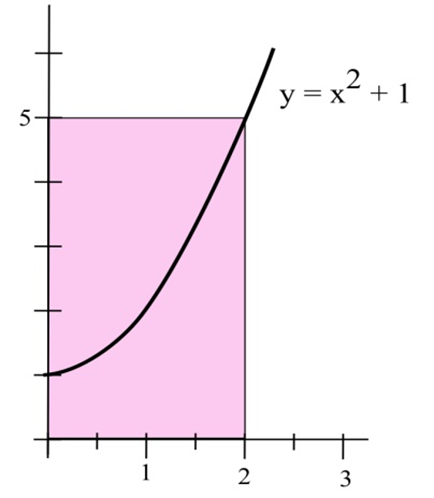
(a) Use Linear Approximation of the area formula to estimate the increase in the area of the rectangle if the base grows from 2 to 2.3 inches.
(b) Calculate exactly the increase in the area of the rectangle as the base grows from 2 to 2.3 inches.
You can measure the diameter of a circle to within 0.3 cm.
(a) How large is the "error" in the calculated area of a circle with a measured diameter of 7.4 cm?
(b) How large is the "error" in the calculated area of a circle with a measured diameter of 13.6 cm?
(c) How large is the percentage error in the calculated area of a circle with a measured diameter of \(d\)?
The demand function for Alicia’s oven mitts is given by \(q=-8p+80\) (\(q\) is the number of oven mitts, \(p\) is the price in dollars). Find the elasticity of demand when \(p =\) $7.50. Will revenue increase if Alicia raises her price from $7.50?
The demand function for Shaki’s danglies is given by \(q=-35p+205\) (\(q\) is the number of danglies, \(p\) is the price in dollars per dangly). Find the elasticity of demand when \(p =\) $5. Should Shaki raise or lower his price to increase revenue?
2.11 Exercises
In problems 1 – 10 find \(dy/dx\) by differentiating implicitly then find the value of \(dy/dx\) at the given point.
| 1. \(x^2 + y^2 = 100\), point (6, 8) | 2. \(x^2 + 5y^2 = 45\), point (5, 2) |
| 3. \(x^2 – 3xy + 7y = 5\), point (2,1) | 4. \(\sqrt{x} + \sqrt{y} = 5\), point (4,9) |
| 5. \(\frac{x^2}{9} + \frac{y^2}{16} = 1\), point (0,4) | 6. \(\frac{x^2}{9} + \frac{y^2}{16} = 1\), point (3,0) |
| 7. \(\ln(y) + 3x – 7 = 0\), point (2,\(e\)) | 8. \(x^2 – y^2 = 16\), point (5,3) |
| 9. \(x^2 – y^2 = 16\), point (5, –3) | 10. \(y^2 + 7x^3 – 3x = 8\), point (1,2) |
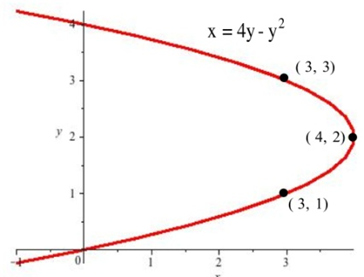
| 11. Find the slopes of the lines tangent to the graph in shown at the points (3,1), (3,3), and (4,2). |
| 12. Find the slopes of the lines tangent to the graph in shown where the graph crosses the \(y\)–axis. |
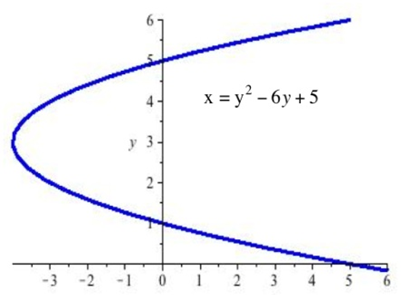
| 13. Find the slopes of the lines tangent to the graph in graph shown at the points ((5,0), (5,6), and (–4,3). |
| 14. Find the slopes of the lines tangent to the graph in the graph shown where the graph crosses the \(y\)–axis. |
In problems 15 – 16, find \(dy/dx\) using implicit differentiation and then find the slope of the line tangent to the graph of the equation at the given point.
| 15. \(y^3 – 5y = 5x^2 + 7\), point (1,3) | 16. \(y^2 – 5xy + x^2 + 21 = 0\), point (2,5) |
An expandable sphere is being filled with liquid at a constant rate from a tap (imagine a water balloon connected to a faucet). When the radius of the sphere is 3 inches, the radius is increasing at 2 inches per minute. How fast is the liquid coming out of the tap? \(( V = \frac{4}{3} \pi r^3 )\)
The 12 inch base of a right triangle is growing at 3 inches per hour, and the 16 inch height is shrinking at 3 inches per hour.
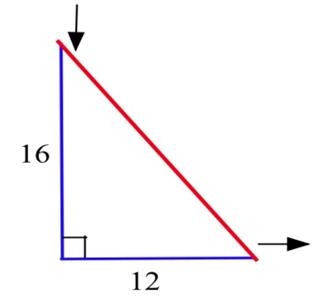
(a) Is the area increasing or decreasing?
(b) Is the perimeter increasing or decreasing?
(c) Is the hypotenuse increasing or decreasing?
One hour later the right triangle in Problem 2 is 15 inches long and 13 inches high, and the base and height are changing at the same rate as in Problem 18.
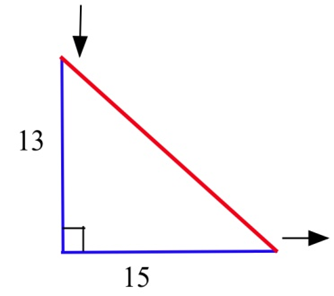
(a) Is the area increasing or decreasing now?
(b) Is the hypotenuse increasing or decreasing now?
(c) Is the perimeter increasing or decreasing now?
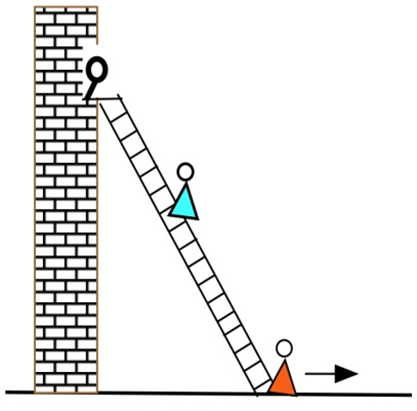
A young woman and her boyfriend plan to elope, but she must rescue him from his mother who has locked him in his room. The young woman has placed a 20 foot long ladder against his house and is knocking on his window when his mother begins pulling the bottom of the ladder away from the house at a rate of 3 feet per second. How fast is the top of the ladder (and the young couple) falling when the bottom of the ladder is
(a) 12 feet from the bottom of the wall?
(b) 16 feet from the bottom of the wall?
(c) 19 feet from the bottom of the wall?
The length of a 12 foot by 8 foot rectangle is increasing at a rate of 3 feet per second and the width is decreasing at 2 feet per second.
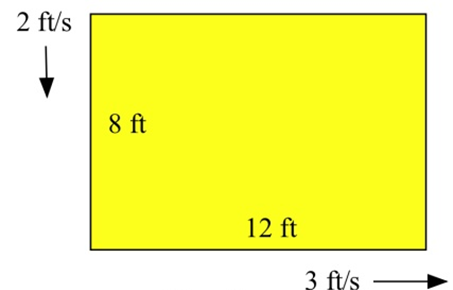
(a) How fast is the perimeter changing?
(b) How fast is the area changing?
An oil tanker in Puget Sound has sprung a leak, and a circular oil slick is forming. The oil slick is 4 inches thick everywhere, is 100 feet in diameter, and the diameter is increasing at 12 feet per hour. Your job, as the Coast Guard commander or the tanker's captain, is to determine how fast the oil is leaking from the tanker.