Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

4.4: The Derivative of sin x - II

  1. Last updated
  2. Save as PDF
  • Page ID
    479

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Now we can complete the calculation of the derivative of the sine:

    \[\eqalign{ {d\over dx}\sin x &= \lim_{\Delta x\to0} {\sin(x+\Delta x)-\sin x \over \Delta x}\cr& =\lim_{\Delta x\to0} \sin x{\cos \Delta x - 1\over \Delta x}+\cos x{\sin\Delta x\over \Delta x}\cr& =\sin x \cdot 0 + \cos x \cdot 1 = \cos x.\cr }\]

    The derivative of a function measures the slope or steepness of the function; if we examine the graphs of the sine and cosine side by side, it should be that the latter appears to accurately describe the slope of the former, and indeed this is true:

    Notice that where the cosine is zero the sine does appear to have a horizontal tangent line, and that the sine appears to be steepest where the cosine takes on its extreme values of 1 and \(-1\). Of course, now that we know the derivative of the sine, we can compute derivatives of more complicated functions involving the sine.

    Example 4.4.1

    Compute the derivative of \(\sin(x^2)\).

    Solution

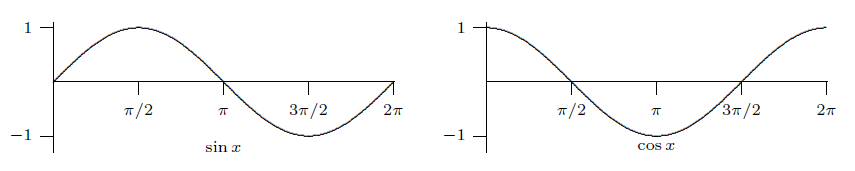
    \[{d\over dx}\sin(x^2) = \cos(x^2)\cdot 2x = 2x\cos(x^2).\]

    Example 4.4.2

    Compute the derivative of \(\sin^2(x^3-5x)\).

    Solution

    \[\eqalign{ {d\over dx}\sin^2(x^3-5x)&={d\over dx}(\sin(x^3-5x))^2\cr& =2(\sin(x^3-5x))^1\cos(x^3-5x)(3x^2-5)\cr& =2(3x^2-5)\cos(x^3-5x)\sin(x^3-5x).\cr }\]

    Contributors

    • Integrated by Justin Marshall.