4.3: A Hard Limit
- Page ID
- 470
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We want to compute this limit:
\[\lim_{\Delta x \to 0} {\sin\Delta x\over \Delta x}.\]
Equivalently, to make the notation a bit simpler, we can compute
\[\lim_{x\to0} {\sin x\over x}.\]
In the original context we need to keep \(x\) and \(\Delta x\) separate, but here it does not hurt to rename \(\Delta x\) to something more convenient. To do this we need to be quite clever, and to employ some indirect reasoning. The indirect reasoning is embodied in a theorem, frequently called the squeeze theorem.
Theorem 4.3.1: The Squeeze Theorem
Suppose that \(g(x) \le f(x) \le h(x)\) for all \(x\) close to \(a\) but not equal to \(a\).
If
\[\lim_{x\to a}g(x)=L=\lim_{x \to a}h(x),\]
then
\[\lim_{x\to a}f(x)=L.\]
This theorem can be proved using the official definition of limit. We won't prove it here, but point out that it is easy to understand and believe graphically. The condition says that \(f(x)\) is trapped between \(g(x)\) below and \(h(x)\) above, and that at \(x=a\), both \(g\) and \(h\) approach the same value. This means the situation looks something like figure 4.3.1.
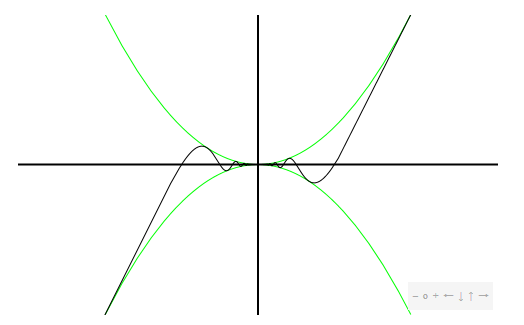
The wiggly curve is \(x^2\sin(\pi/x)\), the upper and lower curves are \(x^2\) and \(-x^2\). Since the sine function is always between \(-1\) and \(1\), \(-x^2\le x^2\sin(\pi/x)\le x^2\), and it is easy to see that \(\lim_{x\to0}-x^2=0=\lim_{x\to0}x^2\). It is not so easy to see directly, that is algebraically, that \(\lim_{x\to0}x^2\sin(\pi/x)=0\), because the \(\pi/x\) prevents us from simply plugging in \(x=0\). The squeeze theorem makes this "hard limit'' as easy as the trivial limits involving \(x^2\).
To do the hard limit that we want, \(\lim_{x\to0} (\sin x)/x\), we will find two simpler functions \(g\) and \(h\) so that \(g(x)\le (\sin x)/x\le h(x)\), and so that \(\lim_{x\to0}g(x)=\lim_{x\to0}h(x)\). Not too surprisingly, this will require some trigonometry and geometry. Referring to figure 4.3.2, \(x\) is the measure of the angle in radians.
Since the circle has radius 1, the coordinates of point \(A\) are \((\cos x,\sin x)\), and the area of the small triangle is \((\cos x\sin x)/2\). This triangle is completely contained within the circular wedge-shaped region bordered by two lines and the circle from \((1,0)\) to point \(A\). Comparing the areas of the triangle and the wedge we see \((\cos x\sin x)/2 \le x/2\), since the area of a circular region with angle \(\theta\) and radius \(r\) is \(\theta r^2/2\). With a little algebra this turns into \((\sin x)/x \le 1/\cos x\), giving us the \(h\) we seek.
Figure 4.3.2: Visualizing \(\sin x / x\).
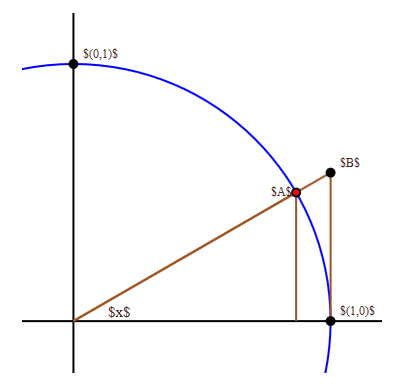
To find \(g\), we note that the circular wedge is completely contained inside the larger triangle. The height of the triangle, from \((1,0)\) to point \(B\), is \(\tan x\), so comparing areas we get \(x/2 \le (\tan x)/2 = \sin x / (2\cos x)\). With a little algebra this becomes \(\cos x \le (\sin x)/x\). So now we have
\[\ \cos x \le {\sin x\over x}\le {1\over\cos x}.\]
Finally, the two limits \(\lim_{x\to0}\cos x\) and \(\lim_{x\to0}1/\cos x\) are easy, because \(\cos(0)=1\). By the squeeze theorem, \(\lim_{x\to0} (\sin x)/x = 1\) as well.
Before we can complete the calculation of the derivative of the sine, we need one other limit: \(\lim_{x\to0}{\cos x - 1\over x}.\) This limit is just as hard as \(\sin x/x\), but closely related to it, so that we don't have to a similar calculation; instead we can do a bit of tricky algebra:
\[{\cos x - 1\over x}={\cos x - 1\over x}{\cos x+1\over\cos x+1} ={\cos^2 x - 1\over x(\cos x+1)}={-\sin^2 x\over x(\cos x+1)}= -{\sin x\over x}{\sin x\over \cos x + 1}.\]
To compute the desired limit it is sufficient to compute the limits of the two final fractions, as \(x\) goes to 0. The first of these is the hard limit we've just done, namely 1. The second turns out to be simple, because the denominator presents no problem:
\[\lim_{x\to0}{\sin x\over \cos x + 1}={\sin 0\over \cos 0+1}= {0\over 2} = 0.\]
Thus,
\[\lim_{x\to0}{\cos x - 1\over x}=0.\]