11.2: Sequences
- Page ID
- 552
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)While the idea of a sequence of numbers, \(a_1,a_2,a_3,\ldots\) is straightforward, it is useful to think of a sequence as a function. We have up until now dealt with functions whose domains are the real numbers, or a subset of the real numbers, like \(f(x)=\sin x\). A sequence is a function with domain the natural numbers \(N=\{1,2,3,\ldots\}\) or the non-negative integers, \(Z^{\ge0}=\{0,1,2,3,\ldots\}\). The range of the function is still allowed to be the real numbers; in symbols, we say that a sequence is a function \(f\colon N \to R\). Sequences are written in a few different ways, all equivalent; these all mean the same thing:
\[ \displaylines{a_1,a_2,a_3,\ldots\cr \left\{a_n\right\}_{n=1}^{\infty}\cr \left\{f(n)\right\}_{n=1}^{\infty}\cr} \nonumber \]
As with functions on the real numbers, we will most often encounter sequences that can be expressed by a formula. We have already seen the sequence \( a_i=f(i)=1-1/2^i\), and others are easy to come by:
\[\eqalign{ f(i)&={i\over i+1}\cr f(n)&={1\over2^n}\cr f(n)&=\sin(n\pi/6)\cr f(i)&={(i-1)(i+2)\over2^i}.\cr } \nonumber \]
Frequently these formulas will make sense if thought of either as functions with domain \(\mathcal{R}\) or \(\mathcal{N}\), though occasionally one will make sense only for integer values.
Faced with a sequence we are interested in the limit \(\lim_{i\to \infty} f(i) = \lim_{i\to\infty} a_i.\) We already understand \(\lim_{x\to\infty} f(x)\) when \(x\) is a real valued variable; now we simply want to restrict the "input'' values to be integers. No real difference is required in the definition of limit, except that we specify, perhaps implicitly, that the variable is an integer. Compare this definition to definition 4.10.2.
Suppose that \(\left\{a_n\right\}_{n=1}^{\infty}\) is a sequence. We say that \( \lim_{n\to \infty}a_n=L\) if for every \(\epsilon>0\) there is an \(N > 0\) so that whenever \(n>N\), \(|a_n-L| < \epsilon\). If \( \lim_{n\to\infty}a_n=L\) we say that the sequence converges, otherwise it diverges.
If \(f(i)\) defines a sequence, and \(f(x)\) makes sense, and \(\displaystyle \lim_{x\to\infty}f(x)=L\), then it is clear that \( \lim_{i\to\infty}f(i)=L\) as well, but it is important to note that the converse of this statement is not true. For example, since \( \lim_{x\to\infty}(1/x)=0\), it is clear that also \( \lim_{i\to\infty}(1/i)=0\), that is, the numbers
\[{1\over1},{1\over2},{1\over3},{1\over4},{1\over5},{1\over6},\ldots \nonumber \]
get closer and closer to 0. Consider this, however: Let \(f(n)=\sin(n\pi)\).
This is the sequence
\[ \sin(0\pi), \sin(1\pi),\sin(2\pi),\sin(3\pi),\ldots=0,0,0,0,\ldots \nonumber \]
since
\[\sin(n\pi)=0 \nonumber \]
when \(n\) is an integer. Thus \( \lim_{n\to\infty}f(n)=0\). But \( \lim_{x\to\infty}f(x)\), when \(x\) is real, does not exist: as \(x\) gets bigger and bigger, the values \(\sin(x\pi)\) do not get closer and closer to a single value, but take on all values between \(-1\) and \(1\) over and over. In general, whenever you want to know \( \lim_{n\to\infty}f(n)\) you should first attempt to compute \( \lim_{x\to\infty}f(x)\), since if the latter exists it is also equal to the first limit. But if for some reason \( \lim_{x\to\infty}f(x)\) does not exist, it may still be true that \( \lim_{n\to\infty}f(n)\) exists, but you'll have to figure out another way to compute it.
It is occasionally useful to think of the graph of a sequence. Since the function is defined only for integer values, the graph is just a sequence of dots. In figure 11.1.1 we see the graphs of two sequences and the graphs of the corresponding real functions.
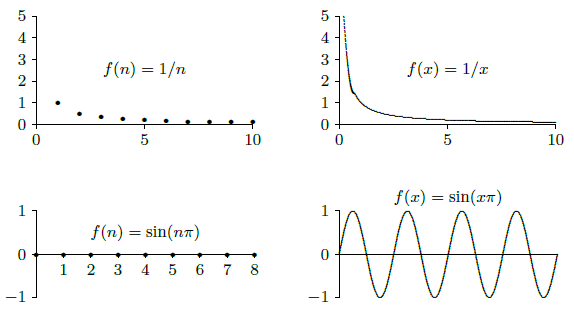
Not surprisingly, the properties of limits of real functions translate into properties of sequences quite easily. Theorem 2.3.6 about limits becomes
Suppose that \(\lim_{n\to\infty}a_n=L\) and \(\lim_{n\to\infty}b_n=M\) and \(k\) is some constant. Then
\[\eqalign{ &\lim_{n\to\infty} ka_n = k\lim_{n\to\infty}a_n=kL\cr &\lim_{n\to\infty} (a_n+b_n) = \lim_{n\to\infty}a_n+\lim_{n\to\infty}b_n=L+M\cr &\lim_{n\to\infty} (a_n-b_n) = \lim_{n\to\infty}a_n-\lim_{n\to\infty}b_n=L-M\cr &\lim_{n\to\infty} (a_nb_n) = \lim_{n\to\infty}a_n\cdot\lim_{n\to\infty}b_n=LM\cr &\lim_{n\to\infty} {a_n\over b_n} = {\lim_{n\to\infty}a_n\over \lim_{n\to\infty}b_n}={L\over M},\hbox{ if \(M\) is not 0}.\cr } \nonumber \]
Likewise the Squeeze Theorem (4.3.1) becomes
Suppose that
\[ a_n \le b_n \le c_n \nonumber \]
for all \(n>N\), for some \(N\). If
\[\lim_{n\to\infty}a_n=\lim_{n\to\infty}c_n=L, \nonumber \]
then
\[\lim_{n\to\infty}b_n=L. \nonumber \]
And a final useful fact:
\[\lim_{n\to\infty}|a_n|=0 \nonumber \]
if and only if
\[\lim_{n\to\infty}a_n=0. \nonumber \]
This theorem says simply that the size of \( a_n\) gets close to zero if and only if \( a_n\) gets close to zero.
Determine whether \(\left\{{n\over n+1}\right\}_{n=0}^{\infty}\) converges or diverges. If it converges, compute the limit.
Solution
Since this makes sense for real numbers we consider
\[ \lim_{x\to\infty}{x\over x+1}=\lim_{x\to\infty}1-{1\over x+1}=1-0=1. \nonumber \]
Thus the sequence converges to 1.
Determine whether \(\bigg\{{\ln n\over n}\bigg\}_{n=1}^{\infty}\) converges or diverges. If it converges, compute the limit.
Solution
We compute \(\lim_{x\to\infty}{\ln x\over x}=\lim_{x\to\infty}{1/x\over 1}= 0,\) using L'Hôpital's Rule. Thus the sequence converges to 0.
Determine whether \(\{(-1)^n\}_{n=0}^{\infty}\) converges or diverges. If it converges, compute the limit.
Solution
This does not make sense for all real exponents, but the sequence is easy to understand: it is \(1,-1,1,-1,1\ldots\) and clearly diverges.
Determine whether \(\{(-1/2)^n\}_{n=0}^{\infty}\) converges or diverges. If it converges, compute the limit.
Solution
We consider the sequence
\[\{|(-1/2)^n|\}_{n=0}^{\infty}=\{(1/2)^n\}_{n=0}^{\infty}. \nonumber \]
Then
\[ \lim_{x\to\infty}\left({1\over2}\right)^x=\lim_{x\to\infty}{1\over2^x}=0, \nonumber \]
so by theorem 11.1.4 the sequence converges to 0.
Determine whether \(\{(\sin n)/\sqrt{n}\}_{n=1}^{\infty}\) converges or diverges. If it converges, compute the limit.
Solution
Since \(|\sin n|\le 1\), \( 0\le|\sin n/\sqrt{n}|\le 1/\sqrt{n}\) and we can use theorem 11.1.3 with \( a_n=0\) and \( c_n=1/\sqrt{n}\). Since \(\lim_{n\to\infty} a_n=\lim_{n\to\infty} c_n=0\), \(\lim_{n\to\infty}\sin n/\sqrt{n}=0\) and the sequence converges to 0.
A particularly common and useful sequence is \( \{r^n\}_{n=0}^{\infty}\), for various values of \(r\). Some are quite easy to understand: If \(r=1\) the sequence converges to 1 since every term is 1, and likewise if \(r=0\) the sequence converges to 0. If \(r=-1\) this is the sequence of example 11.1.7 and diverges. If \(r>1\) or \(r < -1\) the terms \( r^n\) get large without limit, so the sequence diverges. If \(0 < r < 1\) then the sequence converges to 0. If \(-1 < r < 0\) then \( |r^n|=|r|^n\) and \(0 < |r| < 1\), so the sequence \( \{|r|^n\}_{n=0}^{\infty}\) converges to 0, so also \(\{r^n\}_{n=0}^{\infty}\) converges to 0. converges. In summary, \( \{r^n\}\) converges precisely when \(-1 < r\le1\) in which case \( \lim_{n\to\infty} r^n=\cases{ 0& if \(-1 < r < 1\)\cr 1& if \(r=1\).\cr} \)
Sometimes we will not be able to determine the limit of a sequence, but we still would like to know whether it converges. In some cases we can determine this even without being able to compute the limit.
A sequence is called increasing or sometimes strictly increasing if \( a_i < a_{i+1}\) for all \(i\). It is called non-decreasing or sometimes (unfortunately) increasing if \( a_i\le a_{i+1}\) for all \(i\). Similarly a sequence is decreasing if \( a_i>a_{i+1}\) for all \(i\) and non-increasing if \( a_i\ge a_{i+1}\) for all \(i\). If a sequence has any of these properties it is called monotonic.
The sequence
\[ \left\{ \dfrac{2^i-1}{2^i} \right\}_{i=1}^{\infty} = \dfrac{1}{2}, \dfrac{3}{4}, \dfrac{7}{8}, \dfrac{15}{16}, \dots \nonumber \]
is increasing,
and
\[ \left\{ {n+1\over n}\right\}_{i=1}^{\infty}= {2\over1},{3\over2},{4\over3},{5\over4},\ldots \nonumber \]
is decreasing.
A sequence is bounded above if there is some number \(N\) such that \( a_n\le N\) for every \(n\), and bounded below if there is some number \(N\) such that \( a_n\ge N\) for every \(n\). If a sequence is bounded above and bounded below it is bounded. If a sequence \( \{a_n\}_{n=0}^{\infty}\) is increasing or non-decreasing it is bounded below (by \( a_0\)), and if it is decreasing or non-increasing it is bounded above (by \( a_0\)). Finally, with all this new terminology we can state an important theorem.
If a sequence is bounded and monotonic, then it converges.
We will not prove this; the proof appears in many calculus books. It is not hard to believe: suppose that a sequence is increasing and bounded, so each term is larger than the one before, yet never larger than some fixed value \(N\). The terms must then get closer and closer to some value between \( a_0\) and \(N\). It need not be \(N\), since \(N\) may be a "too-generous'' upper bound; the limit will be the smallest number that is above all of the terms \( a_i\).
All of the terms \( (2^i-1)/2^i\) are less than 2, and the sequence is increasing. As we have seen, the limit of the sequence is 1---1 is the smallest number that is bigger than all the terms in the sequence. Similarly, all of the terms \((n+1)/n\) are bigger than \(1/2\), and the limit is 1---1 is the largest number that is smaller than the terms of the sequence.
We do not actually need to know that a sequence is monotonic to apply this theorem---it is enough to know that the sequence is "eventually'' monotonic, that is, that at some point it becomes increasing or decreasing. For example, the sequence \(10\), \(9\), \(8\), \(15\), \(3\), \(21\), \(4\), \(3/4\), \(7/8\), \(15/16\), \(31/32,\ldots\) is not increasing, because among the first few terms it is not. But starting with the term \(3/4\) it is increasing, so the theorem tells us that the sequence \(3/4, 7/8, 15/16, 31/32,\ldots\) converges. Since convergence depends only on what happens as \(n\) gets large, adding a few terms at the beginning can't turn a convergent sequence into a divergent one.
Show that \(\{n^{1/n}\}\) converges.
Solution
We first show that this sequence is decreasing, that is, that \( n^{1/n}> (n+1)^{1/(n+1)}\). Consider the real function \( f(x)=x^{1/x}\) when \(x\ge1\). We can compute the derivative, \( f'(x)=x^{1/x}(1-\ln x)/x^2\), and note that when \(x\ge 3\) this is negative. Since the function has negative slope, \( n^{1/n}> (n+1)^{1/(n+1)}\) when \(n\ge 3\). Since all terms of the sequence are positive, the sequence is decreasing and bounded when \(n\ge3\), and so the sequence converges. (As it happens, we can compute the limit in this case, but we know it converges even without knowing the limit; see exercise 1.)
Show that \(\{n!/n^n\}\) converges.
Solution
Again we show that the sequence is decreasing, and since each term is positive the sequence converges. We can't take the derivative this time, as \(x!\) doesn't make sense for \(x\) real. But we note that if \( a_{n+1}/a_n < 1\) then \( a_{n+1} < a_n\), which is what we want to know. So we look at
\[ a_{n+1}/a_n: {a_{n+1}\over a_n} = {(n+1)!\over (n+1)^{n+1}}{n^n\over n!}= {(n+1)!\over n!}{n^n\over (n+1)^{n+1}}= {n+1\over n+1}\left({n\over n+1}\right)^n= \left({n\over n+1}\right)^n < 1. \nonumber \]
(Again it is possible to compute the limit; see exercise 2.)
Contributors
Integrated by Justin Marshall.


