3.7E: Exercises for Section 3.7
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 4, use the graph of y=f(x) to
a. sketch the graph of y=f−1(x), and
b. use part a. to estimate (f−1)′(1).
1)
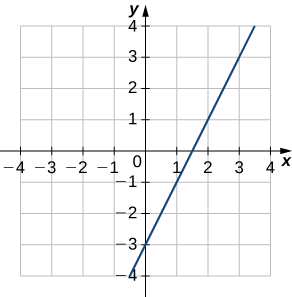
2)
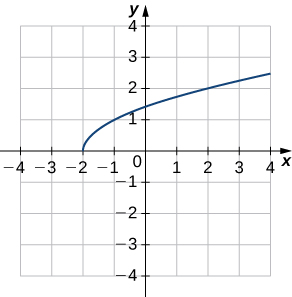
- Answer
-
a.
b. (f−1)′(1)≈2
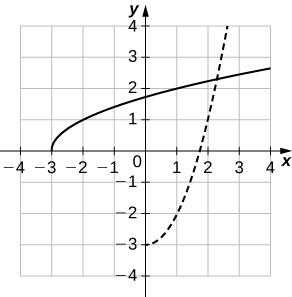
3)
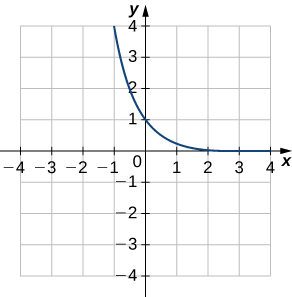
4)
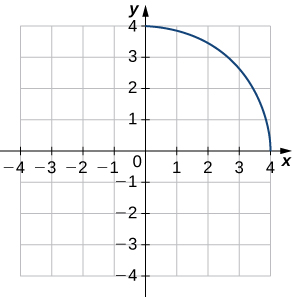
- Answer
-
a.
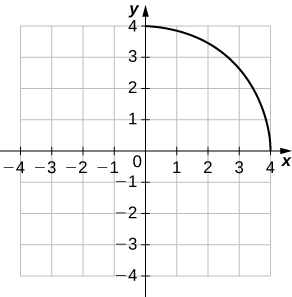
b. (f−1)′(1)≈−1/√3
For exercises 5 - 8, use the given function y=f(x) to find
a. dfdx at x=a and
b. x=f−1(y).
c. Then use part b. to find df−1dy at y=f(a).
5) f(x)=6x−1,x=−2
6) f(x)=2x3−3,x=1
- Answer
- a. dfdx=6
b. x=f−1(y)=(y+32)1/3
c. df−1dy=16
7) f(x)=9−x2,0≤x≤3,x=2
8) f(x)=sinx,x=0
- Answer
- a. dfdx=1
b. x=f−1(y)=sin−1y
c. df−1dy=1
For each function in exercises 9 - 14, find (f−1)′(a).
9) f(x)=x2+3x+2,x≥−1,a=2
10 f(x)=x3+2x+3,a=0
- Answer
- (f−1)′(1)=15
11) f(x)=x+√x,a=2
12) f(x)=x−2x,x<0,a=1
- Answer
- (f−1)′(1)=13
13) f(x)=x+sinx,a=0
14) f(x)=tanx+3x2,a=0
- Answer
- (f−1)′(0)=1
For each function y=f(x), given in exercises 15 - 19,
a. find the slope of the tangent line to its inverse function f−1 at the indicated point P, and
b. find the equation of the tangent line to the graph of f−1 at the indicated point.
15) f(x)=41+x2,P(2,1)
16) f(x)=√x−4,P(2,8)
- Answer
- a. 4
b. y=4x
17) f(x)=(x3+1)4,P(16,1)
18) f(x)=−x3−x+2,P(−8,2)
- Answer
- a. −196
b. y=−113x+1813
19) f(x)=x5+3x3−4x−8,P(−8,1)
In exercises 20 - 29, find dydx for the given function.
20) y=sin−1(x2)
- Answer
- dydx=2x√1−x4
21) y=cos−1(√x)
22) y=sec−1(1x)
- Answer
- dydx=−1√1−x2
23) y=√csc−1x
24) y=(1+tan−1x)3
- Answer
- dydx=3(1+tan−1x)21+x2
25) y=cos−1(2x)⋅sin−1(2x)
26) y=1tan−1(x)
- Answer
- dydx=−1(1+x2)(tan−1x)2
27) y=sec−1(−x)
28) y=cot−1√4−x2
- Answer
- dydx=x(5−x2)√4−x2
29) y=x⋅csc−1x
In exercises 30 - 35, use the given values to find (f−1)′(a).
30) f(π)=0,f′(π)=−1,a=0
- Answer
- (f−1)′(0)=−1
31) f(6)=2,f′(6)=13,a=2
32) f(13)=−8,f′(13)=2,a=−8
- Answer
- (f−1)′(−8)=12
33) f(√3)=12,f′(√3)=23,a=12
34) f(1)=−3,f′(1)=10,a=−3
- Answer
- (f−1)′(−3)=110
35) f(1)=0,f′(1)=−2,a=0
36) [T] The position of a moving hockey puck after t seconds is s(t)=tan−1t where s is in meters.
a. Find the velocity of the hockey puck at any time t.
b. Find the acceleration of the puck at any time t.
c. Evaluate parts a. and b. for t=2,4,and 6 seconds.
d. What conclusion can be drawn from the results in c.?
- Answer
-
a. v(t)=11+t2
b. a(t)=−2t(1+t2)2
c. (a) 0.2,0.06,0.03; (b) −0.16,−0.028,−0.0088d. The hockey puck is decelerating/slowing down at 2, 4, and 6 seconds.
Solution:
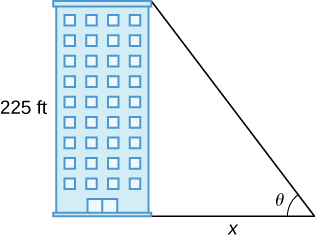
37) [T] A building that is 225 feet tall casts a shadow of various lengths x as the day goes by. An angle of elevation θ is formed by lines from the top and bottom of the building to the tip of the shadow, as seen in the following figure. Find the rate of change of the angle of elevation dθdx when x=272 feet.
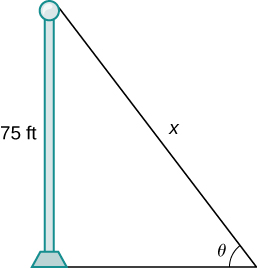
38) [T] A pole stands 75 feet tall. An angle θ is formed when wires of various lengths of x feet are attached from the ground to the top of the pole, as shown in the following figure. Find the rate of change of the angle dθdx when a wire of length 90 feet is attached.
- Answer
- −0.0168 radians per foot
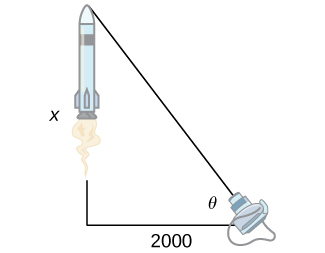
39) [T] A television camera at ground level is 2000 feet away from the launching pad of a space rocket that is set to take off vertically, as seen in the following figure. The angle of elevation of the camera can be found by θ=tan−1(x2000), where x is the height of the rocket. Find the rate of change of the angle of elevation after launch when the camera and the rocket are 5000 feet apart.
40) [T] A local movie theater with a 30-foot-high screen that is 10 feet above a person’s eye level when seated has a viewing angle θ (in radians) given by θ=cot−1x40−cot−1x10,
where x is the distance in feet away from the movie screen that the person is sitting, as shown in the following figure.
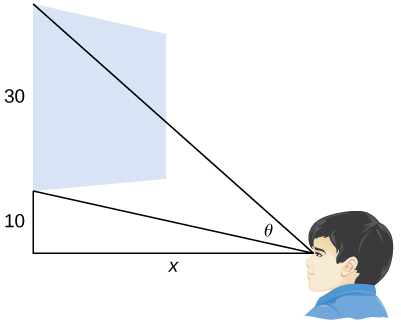
a. Find dθdx.
b. Evaluate dθdx for x=5,10,15, and 20.
c. Interpret the results in part b.
d. Evaluate dθdx for x=25,30,35, and 40.
e. Interpret the results in part d. At what distance x should the person stand to maximize his or her viewing angle?
- Answer
- a. dθdx=10100+x2−401600+x2
b. 18325,9340,424745,0
c. As a person moves farther away from the screen, the viewing angle is increasing, which implies that as he or she moves farther away, his or her screen vision is widening. d. −5412905,−3500,−19829945,−91360
e. As the person moves beyond 20 feet from the screen, the viewing angle is decreasing. The optimal distance the person should stand for maximizing the viewing angle is 20 feet.

