9.5E: Exercises for Section 9.5

In exercises 1 - 30, state whether each of the following series converges absolutely, conditionally, or not at all.

1) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+3}$

2) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}$

Answer

This series diverges by the divergence test. Terms do not tend to zero.

3) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}$

4) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}$

Answer

Converges conditionally by alternating series test, since $\sqrt{n+3}/n$ is decreasing and its limit is 0. Does not converge absolutely by comparison with $p$-series, $p=1/2$.

5) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n!}$

6) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{3^n}{n!}$

Answer

Converges absolutely by limit comparison to $3^n/4^n,$ for example.

7) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n−1}{n}\right)^n$

8) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n+1}{n}\right)^n$

Answer

Diverges by divergence test since $\displaystyle \lim_{n→∞}|a_n|=e$ and not $0$.

9) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2n$

10) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2n$

Answer

Diverges by the divergence test, since its terms do not tend to zero. The limit of the sequence of its terms does not exist.

11) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2(1/n)$

12) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2(1/n)$

Answer

$\displaystyle \lim_{n→∞}\cos^2(1/n)=1.$ Diverges by divergence test.

13) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1/n)$

14) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1+\frac{1}{n})$

Answer

Converges by alternating series test.

15) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}$

16) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^e}{1+n^π}$

Answer

Converges conditionally by alternating series test. Does not converge absolutely by limit comparison with $p$-series, $p=π−e$

Solution:

17) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}2^{1/n}$

18) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}n^{1/n}$

Answer

Diverges; terms do not tend to zero.

19) $\displaystyle \sum^∞_{n=1}(−1)^n(1−n^{1/n})$ (Hint: $n^{1/n}≈1+\ln(n)/n$ for large $n$.)

20) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}n\left(1−\cos\left(\frac{1}{n}\right)\right)$ (Hint: $\cos(1/n)≈1−1/n^2$ for large $n$.)

Answer

Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.

21) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\sqrt{n+1}−\sqrt{n})$ (Hint: Rationalize the numerator.)

22) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}}\right)$ (Hint: Cross-multiply then rationalize numerator.)

Answer

Converges absolutely by limit comparison with $p$-series, $p=3/2$, after applying the hint.

23) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\ln(n+1)−\ln n)$

24) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(\tan^{−1}(n+1)−\tan^{−1}n)$ (Hint: Use Mean Value Theorem.)

Answer

Converges by alternating series test since $n(\tan^{−1}(n+1)−\tan^{−1}n)$ is decreasing to zero for large $n$.Does not converge absolutely by limit comparison with harmonic series after applying hint.

25) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}((n+1)^2−n^2)$

26) $\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{n}−\frac{1}{n+1}\right)$

Answer

Converges absolutely, since $a_n=\dfrac{1}{n}−\dfrac{1}{n+1}$ are terms of a telescoping series.

27) $\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n}$

28) $\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n^{1/n}}$

Answer

Terms do not tend to zero. Series diverges by divergence test.

29) $\displaystyle \sum^∞_{n=1}\frac{1}{n}\sin(\frac{nπ}{2})$

30) $\displaystyle \sum^∞_{n=1}\sin(nπ/2)\sin(1/n)$

Answer

Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.

In exercises 31 - 36, use the estimate $|R_N|≤b_{N+1}$ to find a value of $N$ that guarantees that the sum of the first $N$ terms of the alternating series $\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n$ differs from the infinite sum by at most the given error. Calculate the partial sum $S_N$ for this $N$.

31) [T] $b_n=1/n,$ error $<10^{−5}$

32) [T] $b_n=1/\ln(n), n≥2,$ error $<10^{−1}$

Answer

$\ln(N+1)>10, N+1>e^{10}, N≥22026; S_{22026}=0.0257…$

33) [T] $b_n=1/\sqrt{n},$ error $<10^{−3}$

34) [T] $b_n=1/2^n$, error $<10^{−6}$

Answer

$2^{N+1}>10^6$ or $N+1>6\ln(10)/\ln(2)=19.93.$ or $N≥19; S_{19}=0.333333969…$

35) [T] $b_n=ln(1+\dfrac{1}{n}),$ error $<10^{−3}$

36) [T] $b_n=1/n^2,$ error $<10^{−6}$

Answer

$(N+1)^2>10^6$ or $N>999; S_{1000}≈0.822466.$

For exercises 37 - 45, indicate whether each of the following statements is true or false. If the statement is false, provide an example in which it is false.

37) If $b_n≥0$ is decreasing and $\displaystyle \lim_{n→∞}b_n=0$, then $\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})$ converges absolutely.

38) If $b_n≥0$ is decreasing, then $\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})$ converges absolutely.

Answer

True. $b_n$ need not tend to zero since if $\displaystyle c_n=b_n−\lim b_n$, then $c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.$

39) If $b_n≥0$ and $\displaystyle \lim_{n→∞}b_n=0$ then $\displaystyle \sum_{n=1}^∞(\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})$ converges.

40) If $b_n≥0$ is decreasing and $\displaystyle \sum_{n=1}^∞(b_{3n−2}+b_{3n−1}−b_{3n})$ converges then $\displaystyle \sum_{n=1}^∞b_{3n−2}$ converges.

Answer

True. $b_{3n−1}−b_{3n}≥0,$ so convergence of $\displaystyle \sum b_{3n−2}$ follows from the comparison test.

41) If $b_n≥0$ is decreasing and $\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n$ converges conditionally but not absolutely, then $b_n$ does not tend to zero.

42) Let $a^+_n=a_n$ if $a_n≥0$ and $a^−_n=−a_n$ if $a_n<0$. (Also, $a^+_n=0$ if $a_n<0$ and $a^−_n=0$ if $a_n≥0$.) If $\displaystyle \sum_{n=1}^∞a_n$ converges conditionally but not absolutely, then neither $\displaystyle \sum_{n=1}^∞a^+_n$ nor $\displaystyle \sum_{n=1}^∞a^−_n$ converge.

Answer

True. If one converges, then so must the other, implying absolute convergence.

43) Suppose that $a_n$ is a sequence of positive real numbers and that $\displaystyle \sum_{n=1}^∞a_n$ converges.

44) Suppose that $b_n$ is an arbitrary sequence of ones and minus ones. Does $\displaystyle \sum_{n=1}^∞a_nb_n$ necessarily converge?

45) Suppose that $a_n$ is a sequence such that $\displaystyle \sum_{n=1}^∞a_nb_n$ converges for every possible sequence $b_n$ of zeros and ones. Does $\displaystyle \sum_{n=1}^∞a_n$ converge absolutely?

Answer

Yes. Take $b_n=1$ if $a_n≥0$ and $b_n=0$ if $a_n<0$. Then $\displaystyle \sum_{n=1}^∞a_nb_n=\sum_{n:a_n≥0}a_n$ converges. Similarly, one can show $\displaystyle \sum_{n:a_n<0}a_n$ converges. Since both series converge, the series must converge absolutely.

In exercises 46 - 49, the series do not satisfy the hypotheses of the alternating series test as stated. In each case, state which hypothesis is not satisfied. State whether the series converges absolutely.

46) $\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\sin^2n}{n}$

47) $\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\cos^2n}{n}$

Answer

Not decreasing. Does not converge absolutely.

48) $\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+⋯$

49) $\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+⋯$

Answer

Not alternating. Can be expressed as $\displaystyle \sum_{n=1}^∞\left(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}\right),$ which diverges by comparison with $\displaystyle \sum_{n=1}^∞\frac{1}{3n−2}.$

50) Show that the alternating series $\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}{8}+⋯$ does not converge. What hypothesis of the alternating series test is not met?

51) Suppose that $\displaystyle \sum a_n$ converges absolutely. Show that the series consisting of the positive terms $a_n$ also converges.

Answer

Let $a^+_n=a_n$ if $a_n≥0$ and $a^+_n=0$ if $a_n<0$. Then $a^+_n≤|a_n|$ for all $n$ so the sequence of partial sums of $a^+_n$ is increasing and bounded above by the sequence of partial sums of $|a_n|$, which converges; hence, $\displaystyle \sum_{n=1}^∞a^+_n$ converges.

52) Show that the alternating series $\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+⋯$ does not converge. What hypothesis of the alternating series test is not met?

53) The formula $\displaystyle \cos θ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯$ will be derived in the next chapter. Use the remainder $|R_N|≤b_{N+1}$ to find a bound for the error in estimating $\cos θ$ by the fifth partial sum $1−θ^2/2!+θ^4/4!−θ^6/6!+θ^8/8!$ for $θ=1, θ=π/6,$ and $θ=π.$

Answer

For $N=5$ one has $∣R_N∣b_6=θ^{10}/10!$. When $θ=1, R_5≤1/10!≈2.75×10^{−7}$. When $θ=π/6,$ $R_5≤(π/6)^{10}/10!≈4.26×10^{−10}$. When $θ=π, R_5≤π^{10}/10!=0.0258.$

54) The formula $\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯$ will be derived in the next chapter. Use the remainder $|R_N|≤b_{N+1}$ to find a bound for the error in estimating $\sin θ$ by the fifth partial sum $θ−θ^3/3!+θ^5/5!−θ^7/7!+θ^9/9!$ for $θ=1, θ=π/6,$ and $θ=π.$

55) How many terms in $\cos θ=1−\dfrac{θ^2}{2!}+\dfrac{θ^4}{4!}−\dfrac{θ^6}{6!}+⋯$ are needed to approximate $\cos 1$ accurate to an error of at most $0.00001$?

Answer

Let $b_n=1/(2n−2)!.$ Then $R_N≤1/(2N)!<0.00001$ when $(2N)!>10^5$ or $N=5$ and $\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325…$, whereas $\cos 1=0.5403023…$

56) How many terms in $\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯$ are needed to approximate $\sin 1$ accurate to an error of at most $0.00001?$

57) Sometimes the alternating series $\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n$ converges to a certain fraction of an absolutely convergent series $\displaystyle \sum_{n=1}^∞b_n$ at a faster rate. Given that $\displaystyle \sum_{n=1}^∞\frac{1}{n^2}=\frac{π^2}{6}$, find $\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+⋯$. Which of the series $\displaystyle 6\sum_{n=1}^∞\frac{1}{n^2}$ and $\displaystyle S\sum_{n=1}^∞\frac{(−1)^{n−1}}{n^2}$ gives a better estimation of $π^2$ using $1000$ terms?

Answer

Let $\displaystyle T=\sum\frac{1}{n^2}.$ Then $T−S=\dfrac{1}{2}T$, so $S=T/2$. $\displaystyle \sqrt{6×\sum_{n=1}^{1000}1/n^2}=3.140638…; \sqrt{\frac{1}{2}×\sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591…; π=3.141592….$ The alternating series is more accurate for $1000$ terms.

The alternating series in exercises 58 & 59 converge to given multiples of $π$. Find the value of $N$ predicted by the remainder estimate such that the $N^{\text{th}}$ partial sum of the series accurately approximates the left-hand side to within the given error. Find the minimum $N$ for which the error bound holds, and give the desired approximate value in each case. Up to 15 decimals places, $π=3.141592653589793….$

58) [T] $\displaystyle \frac{π}{4}=\sum_{n=0}^∞\frac{(−1)^n}{2n+1},$ error $<0.0001$

59) [T] $\displaystyle \frac{π}{\sqrt{12}}=\sum_{k=0}^∞\frac{(−3)^{−k}}{2k+1},$ error $<0.0001$

Answer

$N=6, S_N=0.9068$

60) [T] The series $\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}$ plays an important role in signal processing. Show that $\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}$ converges whenever $0<x<π$. (Hint: Use the formula for the sine of a sum of angles.)

61) [T] If $\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n}→ln2,$ what is $\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+⋯?$

Answer

$\ln(2).$ The $n^{\text{th}}$ partial sum is the same as that for the alternating harmonic series.

62) [T] Plot the series $\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}$ for $0≤x<1$. Explain why $\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}$ diverges when $x=0,1$. How does the series behave for other $x$?

63) [T] Plot the series $\displaystyle \sum_{n=1}^{100}\frac{\sin(2πnx)}{n}$ for $0≤x<1$ and comment on its behavior

Answer

The series jumps rapidly near the endpoints. For $x$ away from the endpoints, the graph looks like $π(1/2−x)$.

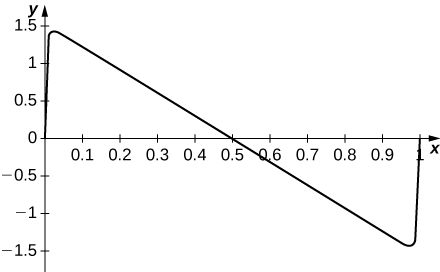
64) [T] Plot the series $\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n^2}$ for $0≤x<1$ and describe its graph.

65) [T] The alternating harmonic series converges because of cancelation among its terms. Its sum is known because the cancelation can be described explicitly. A random harmonic series is one of the form $\displaystyle \sum_{n=1}^∞\frac{S_n}{n}$, where $s_n$ is a randomly generated sequence of $±1's$ in which the values $±1$ are equally likely to occur. Use a random number generator to produce $1000$ random $±1's$ and plot the partial sums $\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}$ of your random harmonic sequence for $N=1$ to $1000$. Compare to a plot of the first $1000$ partial sums of the harmonic series.

Answer

Here is a typical result. The top curve consists of partial sums of the harmonic series. The bottom curve plots partial sums of a random harmonic series.

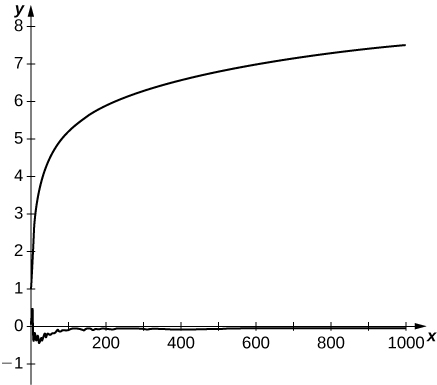
66) [T] Estimates of $\displaystyle \sum_{n=1}^∞\frac{1}{n^2}$ can be accelerated by writing its partial sums as $\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}$ and recalling that $\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}$ converges to one as $N→∞.$ Compare the estimate of $π^2/6$ using the sums $\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}$ with the estimate using $\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}$.

67) [T] The Euler transform rewrites $\displaystyle S=\sum_{n=0}^∞(−1)^nb_n$ as $\displaystyle S=\sum_{n=0}^∞(−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}$. For the alternating harmonic series, it takes the form $\displaystyle \ln(2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}=\sum_{n=1}^∞\frac{1}{n2^n}$. Compute partial sums of $\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}$ until they approximate $\ln(2)$ accurate to within $0.0001$. How many terms are needed? Compare this answer to the number of terms of the alternating harmonic series are needed to estimate $\ln(2)$.

Answer

By the alternating series test, $|S_n−S|≤b_{n+1},$ so one needs $10^4$ terms of the alternating harmonic series to estimate $\ln(2)$ to within $0.0001$. The first $10$ partial sums of the series $\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}$ are (up to four decimals) $0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931$ and the tenth partial sum is within $0.0001$ of $\ln(2)=0.6931….$

68) [T] In the text it was stated that a conditionally convergent series can be rearranged to converge to any number. Here is a slightly simpler, but similar, fact. If $a_n≥0$ is such that $a_n→0$ as $n→∞$ but $\displaystyle \sum_{n=1}^∞a_n$ diverges, then, given any number $A$ there is a sequence $s_n$ of $±1's$ such that $\displaystyle \sum_{n=1}^∞a_ns_n→A.$ Show this for $A>0$ as follows.

a. Recursively define $s_n$ by $s_n=1$ if $\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A$ and $s_n=−1$ otherwise.

b. Explain why eventually $S_n≥A,$ and for any $m$ larger than this $n$, $A−a_m≤S_m≤A+a_m$.

c. Explain why this implies that $S_n→A$ as $n→∞.$