9.4: Comparison Tests

Learning Objectives

• Use the comparison test to test a series for convergence.
• Use the limit comparison test to determine convergence of a series.

We have seen that the integral test allows us to determine the convergence or divergence of a series by comparing it to a related improper integral. In this section, we show how to use comparison tests to determine the convergence or divergence of a series by comparing it to a series whose convergence or divergence is known. Typically these tests are used to determine convergence of series that are similar to geometric series or \(p\)-series.

Comparison Test

In the preceding two sections, we discussed two large classes of series: geometric series and \(p\)-series. We know exactly when these series converge and when they diverge. Here we show how to use the convergence or divergence of these series to prove convergence or divergence for other series, using a method called the comparison test.

For example, consider the series

\[\sum_{n=1}^∞\dfrac{1}{n^2+1}. \nonumber \]

This series looks similar to the convergent series

\[\sum_{n=1}^∞\dfrac{1}{n^2} \nonumber \]

Since the terms in each of the series are positive, the sequence of partial sums for each series is monotone increasing. Furthermore, since

\[0<\dfrac{1}{n^2+1}<\dfrac{1}{n^2} \nonumber \]

for all positive integers \(n\), the \(k^{\text{th}}\) partial sum \(S_k\) of \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2+1}\) satisfies

\[S_k=\sum_{n=1}^k\dfrac{1}{n^2+1}<\sum_{n=1}^k\dfrac{1}{n^2}<\sum_{n=1}^∞\dfrac{1}{n^2}. \nonumber \]

(See Figure \(\PageIndex{1a}\) and Table \(\PageIndex{1}\).) Since the series on the right converges, the sequence \({S_k}\) is bounded above. We conclude that \({S_k}\) is a monotone increasing sequence that is bounded above. Therefore, by the Monotone Convergence Theorem, \({S_k}\) converges, and thus

\[\sum_{n=1}^∞\dfrac{1}{n^2+1} \nonumber \]

converges.

Similarly, consider the series

\[\sum_{n=1}^∞\dfrac{1}{n−1/2}. \nonumber \]

This series looks similar to the divergent series

\[\sum_{n=1}^∞\dfrac{1}{n}. \nonumber \]

The sequence of partial sums for each series is monotone increasing and

\[\dfrac{1}{n−1/2}>\dfrac{1}{n}>0 \nonumber \]

for every positive integer \(n\). Therefore, the \(k^{\text{th}}\) partial sum \(S_k\) of

\[ \sum^∞_{n=1}\dfrac{1}{n−1/2} \nonumber \]

satisfies

\[S_k=\sum_{n=1}^k\dfrac{1}{n−1/2}>\sum_{n=1}^k\dfrac{1}{n}. \nonumber \]

(See Figure \(\PageIndex{1n}\) and Table \(\PageIndex{1}\)). Since the series \(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) diverges to infinity, the sequence of partial sums \(\displaystyle \sum^k_{n=1}\frac{1}{n}\) is unbounded. Consequently, \({S_k}\) is an unbounded sequence, and therefore diverges. We conclude that

\[\sum_{n=1}^∞\dfrac{1}{n−1/2} \nonumber \]

diverges.

Figure \(\PageIndex{1}\): (a) Each of the partial sums for the given series is less than the corresponding partial sum for the converging \(p−series\). (b) Each of the partial sums for the given series is greater than the corresponding partial sum for the diverging harmonic series.

Table \(\PageIndex{1}\): Comparing a series with a \(p\)-series (\(p = 2\))

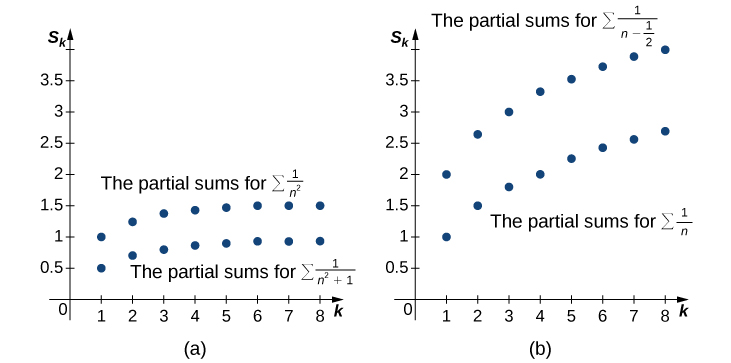
\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2+1}\)	0.5	0.7	0.8	0.8588	0.8973	0.9243	0.9443	0.9597
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2}\)	1	1.25	1.3611	1.4236	1.4636	1.4914	1.5118	1.5274

Table \(\PageIndex{2}\): Comparing a series with the harmonic series

\(k\)	1	2	3	4	5	6	7	8
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n−1/2}\)	2	2.6667	3.0667	3.3524	3.5746	3.7564	3.9103	4.0436
\(\displaystyle \sum_{n=1}^k\dfrac{1}{n}\)	1	1.5	1.8333	2.0933	2.2833	2.45	2.5929	2.7179

Comparison Test

1. Suppose there exists an integer \(N\) such that \(0≤a_n≤b_n\) for all \(n≥N\). If \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges.
2. Suppose there exists an integer \(N\) such that \(a_n≥b_n≥0\) for all \(n≥N.\) If \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.

Proof

We prove part i. The proof of part ii. is the contrapositive of part i. Let \({S_k}\) be the sequence of partial sums associated with \(\displaystyle \sum^∞_{n=1}a_n\), and let \(\displaystyle L=\sum^∞_{n=1}b_n\). Since the terms \(a_n≥0,\)

\[S_k=a_1+a_2+⋯+a_k≤a_1+a_2+⋯+a_k+a_{k+1}=S_{k+1}. \nonumber \]

Therefore, the sequence of partial sums is increasing. Further, since \(a_n≤b_n\) for all \(n≥N\), then

\[\sum_{n=N}^ka_n≤\sum_{n=N}^kb_n≤\sum_{n=1}^∞b_n=L. \nonumber \]

Therefore, for all \(k≥1\),

\[S_k=(a_1+a_2+⋯+a_{N−1})+\sum_{n=N}^ka_n≤(a_1+a_2+⋯+a_{N−1})+L. \nonumber \]

Since \(a_1+a_2+⋯+a_{N−1}\) is a finite number, we conclude that the sequence \({S_k}\) is bounded above. Therefore, \({S_k}\) is an increasing sequence that is bounded above. By the Monotone Convergence Theorem, we conclude that \({S_k}\) converges, and therefore the series \(\displaystyle \sum_{n=1}^∞a_n\) converges.

□

To use the comparison test to determine the convergence or divergence of a series \(\displaystyle \sum_{n=1}^∞a_n\), it is necessary to find a suitable series with which to compare it. Since we know the convergence properties of geometric series and \(p\)-series, these series are often used. If there exists an integer \(N\) such that for all \(n≥N\), each term an is less than each corresponding term of a known convergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) converges. Similarly, if there exists an integer \(N\) such that for all \(n≥N\), each term an is greater than each corresponding term of a known divergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) diverges.

Example \(\PageIndex{1}\): Using the Comparison Test

For each of the following series, use the comparison test to determine whether the series converges or diverges.

1. \(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3+3n+1}\)
2. \(\displaystyle \sum_{n=1}^∞\dfrac{1}{2^n+1}\)
3. \(\displaystyle \sum_{n=2}^∞\dfrac{1}{\ln \,n }\)

Solution

a. Compare to \(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\). Since \(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\) is a \(p\)-series with \(p=3\), it converges. Further,

\[\dfrac{1}{n^3+3n+1}<\dfrac{1}{n^3} \nonumber \]

for every positive integer \(n\). Therefore, we can conclude that \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^3+3n+1}\) converges.

b. Compare to \(\displaystyle \sum^∞_{n=1}\left(\dfrac{1}{2}\right)^n\). Since \(\displaystyle \sum_{n=1}^∞\left(\dfrac{1}{2}\right)^n\) is a geometric series with \(r=\dfrac{1}{2}\) and \(\left|\dfrac{1}{2}\right|<1\), it converges. Also,

\[\dfrac{1}{2^n+1}<\dfrac{1}{2^n} \nonumber \]

for every positive integer \(n\). Therefore, we see that \(\displaystyle \sum^∞_{n=1}\dfrac{1}{2^n+1}\) converges.

c. Compare to \(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\). Since

\[\dfrac{1}{\ln n }>\dfrac{1}{n} \nonumber \]

for every integer \(n≥2\) and \(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\) diverges, we have that \(\displaystyle \sum^∞_{n=2}\dfrac{1}{\ln n}\) diverges.

Exercise \(\PageIndex{1}\)

Use the comparison test to determine if the series \(\displaystyle \sum^∞_{n=1}\dfrac{n}{n^3+n+1}\) converges or diverges.

Hint

Find a value \(p\) such that \(\dfrac{n}{n^3+n+1}≤\dfrac{1}{n^p}\).

Answer

The series converges.

Limit Comparison Test

The comparison test works nicely if we can find a comparable series satisfying the hypothesis of the test. However, sometimes finding an appropriate series can be difficult. Consider the series

\[\sum_{n=2}^∞\dfrac{1}{n^2−1}. \nonumber \]

It is natural to compare this series with the convergent series

\[\sum_{n=2}^∞\dfrac{1}{n^2}. \nonumber \]

However, this series does not satisfy the hypothesis necessary to use the comparison test because

\[\dfrac{1}{n^2−1}>\dfrac{1}{n^2} \nonumber \]

for all integers \(n≥2\). Although we could look for a different series with which to compare \(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1},\) instead we show how we can use the limit comparison test to compare

\[\sum_{n=2}^∞\frac{1}{n^2−1} \nonumber \]

and

\[\sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]

Let us examine the idea behind the limit comparison test. Consider two series \(\displaystyle \sum^∞_{n=1}a_n\) and \(\displaystyle \sum^∞_{n=1}b_n\). with positive terms \(a_n\) and \(b_n\) and evaluate

\[\lim_{n→∞}\frac{a_n}{b_n}. \nonumber \]

If

\[\lim_{n→∞}\frac{a_n}{b_n}=L≠0, \nonumber \]

then, for \(n\) sufficiently large, \(a_n≈Lb_n\). Therefore, either both series converge or both series diverge. For the series \(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1}\) and \(\displaystyle \sum^∞_{n=2}\dfrac{1}{n^2}\), we see that

\[\lim_{n→∞}\dfrac{1/(n^2−1)}{1/n^2}=\lim_{n→∞}\dfrac{n^2}{n^2−1}=1. \nonumber \]

Since \(\displaystyle \sum^∞_{n=2}\frac{1}{n^2}\) converges, we conclude that

\[\sum_{n=2}^∞\dfrac{1}{n^2−1} \nonumber \]

converges.

The limit comparison test can be used in two other cases. Suppose

\[\lim_{n→∞}\dfrac{a_n}{b_n}=0. \nonumber \]

In this case, \({a_n/b_n}\) is a bounded sequence. As a result, there exists a constant \(M\) such that \(a_n≤Mb_n\). Therefore, if \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges. On the other hand, suppose

\[\lim_{n→∞}\dfrac{a_n}{b_n}=∞. \nonumber \]

In this case, \({a_n/b_n}\) is an unbounded sequence. Therefore, for every constant \(M\) there exists an integer \(N\) such that \(a_n≥Mb_n\) for all \(n≥N.\) Therefore, if \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges as well.

Limit Comparison Test

Let \(a_n,b_n≥0\) for all \(n≥1.\)

1. If \(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=L≠0,\) then \(\displaystyle \sum^∞_{n=1}a_n\) and \(\displaystyle \sum^∞_{n=1}b_n\) both converge or both diverge.
2. If \(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=0\) and \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges.
3. If \(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=∞\) and \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.

Note that if \(\dfrac{a_n}{b_n}→0\) and \(\displaystyle \sum^∞_{n=1}b_n\) diverges, the limit comparison test gives no information. Similarly, if \(\dfrac{a_n}{b_n}→∞\) and \(\displaystyle \sum^∞_{n=1}b_n\) converges, the test also provides no information. For example, consider the two series \(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) and \(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). These series are both \(p\)-series with \(p=\frac{1}{2}\) and \(p=2\), respectively. Since \(p=\frac{1}{2}<1,\) the series \(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) diverges. On the other hand, since \(p=2>1\), the series \(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) converges. However, suppose we attempted to apply the limit comparison test, using the convergent \(p\)−series \(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\) as our comparison series. First, we see that

\[\dfrac{1/\sqrt{n}}{1/n^3}=\dfrac{n^3}{\sqrt{n}}=n^{5/2}→∞\; \text{ as } \;n→∞. \nonumber \]

Similarly, we see that

\[\dfrac{1/n^2}{1/n^3}=n→∞\; \text{ as } \;n→∞. \nonumber \]

Therefore, if \(\dfrac{a_n}{b_n}→∞\) when \(\displaystyle \sum_{n=1}^∞b_n\) converges, we do not gain any information on the convergence or divergence of \(\displaystyle \sum_{n=1}^∞a_n\).

Example \(\PageIndex{2}\): Using the Limit Comparison Test

For each of the following series, use the limit comparison test to determine whether the series converges or diverges. If the test does not apply, say so.

1. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\)
2. \(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\)
3. \(\displaystyle \sum^∞_{n=1}\dfrac{\ln(n)}{n^2}\)

Solution

a. Compare this series to \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\). Calculate

\(\displaystyle \lim_{n→∞}\dfrac{1/(\sqrt{n}+1)}{1/\sqrt{n}}=\lim_{n→∞}\dfrac{\sqrt{n}}{\sqrt{n}+1}=\lim_{n→∞}\dfrac{1/\sqrt{n}}{1+1/\sqrt{n}}=1.\)

By the limit comparison test, since \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\) diverges, then \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\) diverges.

b. Compare this series to \(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\). We see that

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=\lim_{n→∞}\dfrac{2^n+1}{3^n}⋅\dfrac{3^n}{2^n}=\lim_{n→∞}\dfrac{2^n+1}{2^n}=\lim_{n→∞}\left[1+\left(\tfrac{1}{2}\right)^n\right]=1.\)

Therefore,

\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=1.\)

Since \(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\) converges, we conclude that \(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\) converges.

c. Since \(\ln n<n,\) compare with \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\). We see that

\(\displaystyle \lim_{n→∞}\dfrac{\ln n/n^2}{1/n}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n}{1}=\lim_{n→∞}\dfrac{\ln n}{n}.\)

In order to evaluate \(\displaystyle \lim_{n→∞}\ln n/n\), evaluate the limit as \(x→∞\) of the real-valued function \(\ln(x)/x\). These two limits are equal, and making this change allows us to use L’Hôpital’s rule. We obtain

\(\displaystyle \lim_{x→∞}\dfrac{lnx}{x}=\lim_{x→∞}\dfrac{1}{x}=0.\)

Therefore, \(\displaystyle \lim_{n→∞}\frac{\ln n}{n}=0\), and, consequently,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n}=0.\)

Since the limit is \(0\) but \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\) diverges, the limit comparison test does not provide any information.

Compare with \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) instead. In this case,

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^2}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^2}{1}=\lim_{n→∞}\ln n=∞.\)

Since the limit is \(∞\) but \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) converges, the test still does not provide any information.

So now we try a series between the two we already tried. Choosing the series \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\), we see that

\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^{3/2}}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^{3/2}}{1}=\lim_{n→∞}\dfrac{\ln n}{\sqrt{n}}\).

As above, in order to evaluate \(\displaystyle \lim_{n→∞}\frac{\ln n}{\sqrt{n}}\), evaluate the limit as \(x→∞\) of the real-valued function \(\frac{\ln n}{\sqrt{n}}\). Using L’Hôpital’s rule,

\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{\sqrt{x}}=\lim_{x→∞}\dfrac{2\sqrt{x}}{x}=\lim_{x→∞}\dfrac{2}{\sqrt{x}}=0\).

Since the limit is \(0\) and \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\) converges, we can conclude that \(\displaystyle \sum^∞_{n=1}\dfrac{\ln n}{n^2}\) converges.

Exercise \(\PageIndex{2}\)

Use the limit comparison test to determine whether the series \(\displaystyle \sum^∞_{n=1}\dfrac{5^n}{3^n+2}\) converges or diverges.

Hint

Compare with a geometric series.

Answer

The series diverges.

Key Concepts

• The comparison tests are used to determine convergence or divergence of series with positive terms.
• When using the comparison tests, a series \(\displaystyle \sum^∞_{n=1}a_n\) is often compared to a geometric or \(p\)-series.

Glossary

comparison test

If \(0≤a_n≤b_n\) for all \(n≥N\) and \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges; if \(a_n≥b_n≥0\) for all \(n≥N\) and \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.

limit comparison test

Suppose \(a_n,b_n≥0\) for all \(n≥1\). If \(\displaystyle \lim_{n→∞}a_n/b_n→L≠0\), then \(\displaystyle \sum^∞_{n=1}a_n\) and \(\displaystyle \sum^∞_{n=1}b_n\) both converge or both diverge; if \(\displaystyle \lim_{n→∞}a_n/b_n→0\) and \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges. If \(\displaystyle \lim_{n→∞}a_n/b_n→∞\), and \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.