10.1: Power Series and Functions

Learning Objectives

• Identify a power series and provide examples of them.
• Determine the radius of convergence and interval of convergence of a power series.
• Use a power series to represent a function.

A power series is a type of series with terms involving a variable. More specifically, if the variable is \(x\), then all the terms of the series involve powers of \(x\). As a result, a power series can be thought of as an infinite polynomial. Power series are used to represent common functions and also to define new functions. In this section we define power series and show how to determine when a power series converges and when it diverges. We also show how to represent certain functions using power series.

Form of a Power Series

A series of the form

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots , \nonumber \]

where \(x\) is a variable and the coefficients \(c_n\) are constants, is known as a power series. The series

\[1+x+x^2+\ldots =\sum_{n=0}^∞x^n \nonumber \]

is an example of a power series. Since this series is a geometric series with ratio \(r=|x|\), we know that it converges if \(|x|<1\) and diverges if \(|x|≥1.\)

Definition \(\PageIndex{1}\): Power Series

A series of the form

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots \nonumber \]

is a power series centered at \(x=0.\) A series of the form

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

is a power series centered at \(x=a\).

To make this definition precise, we stipulate that \(x^0=1\) and \((x−a)^0=1\) even when \(x=0\) and \(x=a\), respectively.

The series

\[\sum_{n=0}^∞\dfrac{x^n}{n!}=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots \nonumber \]

and

\[\sum_{n=0}^∞n!x^n=1+x+2!x^2+3!x^3+\ldots \nonumber \]

are both power series centered at \(x=0.\) The series

\[\sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}=1+\dfrac{x−2}{2⋅3}+\dfrac{(x−2)^2}{3⋅3^2}+\dfrac{(x−2)^3}{4⋅3^3}+\ldots \nonumber \]

is a power series centered at \(x=2\).

Convergence of a Power Series

Since the terms in a power series involve a variable \(x\), the series may converge for certain values of \(x\) and diverge for other values of \(x\). For a power series centered at \(x=a\), the value of the series at \(x=a\) is given by \(c_0\). Therefore, a power series always converges at its center. Some power series converge only at that value of \(x\). Most power series, however, converge for more than one value of \(x\). In that case, the power series either converges for all real numbers \(x\) or converges for all \(x\) in a finite interval. For example, the geometric series \(\displaystyle \sum_{n=0}^∞x^n\) converges for all \(x\) in the interval \((−1,1)\), but diverges for all \(x\) outside that interval. We now summarize these three possibilities for a general power series.

Note \(\PageIndex{1}\): Convergence of a Power Series

Consider the power series \(\displaystyle \sum_{n=0}^∞c_n(x−a)^n.\) The series satisfies exactly one of the following properties:

1. The series converges at \(x=a\) and diverges for all \(x≠a.\)
2. The series converges for all real numbers \(x\).
3. There exists a real number \(R>0\) such that the series converges if \(|x−a|<R\) and diverges if \(|x−a|>R\). At the values \(x\) where \(|x−a|=R\), the series may converge or diverge.

Proof

Suppose that the power series is centered at \(a=0\). (For a series centered at a value of \(a\) other than zero, the result follows by letting \(y=x−a\) and considering the series

\[ \sum_{n=1}^∞c_ny^n. \nonumber \]

We must first prove the following fact:

If there exists a real number \(d≠0\) such that \(\displaystyle \sum_{n=0}^∞c_nd^n\) converges, then the series \(\displaystyle \sum_{n=0}^∞c_nx^n\) converges absolutely for all \(x\) such that \(|x|<|d|.\)

Since \(\displaystyle \sum_{n=0}^∞c_nd^n\) converges, the nth term \(c_nd^n→0\) as \(n→∞\). Therefore, there exists an integer \(N\) such that \(|c_nd^n|≤1\) for all \(n≥N.\) Writing

\[|c_nx^n|=|c_nd^n| \left|\dfrac{x}{d}\right|^n, \nonumber \]

we conclude that, for all n≥N,

\[|c_nx^n|≤\left|\dfrac{x}{d}\right|^n. \nonumber \]

The series

\[\sum_{n=N}^∞\left|\dfrac{x}{d}\right|^n \nonumber \]

is a geometric series that converges if \(|\dfrac{x}{d}|<1.\) Therefore, by the comparison test, we conclude that \(\displaystyle \sum_{n=N}^∞c_nx^n\) also converges for \(|x|<|d|\). Since we can add a finite number of terms to a convergent series, we conclude that \(\displaystyle \sum_{n=0}^∞c_nx^n\) converges for \(|x|<|d|.\)

With this result, we can now prove the theorem. Consider the series

\[\sum_{n=0}^∞a_nx^n \nonumber \]

and let \(S\) be the set of real numbers for which the series converges. Suppose that the set \(S={0}.\) Then the series falls under case i.

Suppose that the set \(S\) is the set of all real numbers. Then the series falls under case ii. Suppose that \(S≠{0}\) and \(S\) is not the set of real numbers. Then there exists a real number \(x*≠0\) such that the series does not converge. Thus, the series cannot converge for any \(x\) such that \(|x|>|x*|\). Therefore, the set \(S\) must be a bounded set, which means that it must have a smallest upper bound. (This fact follows from the Least Upper Bound Property for the real numbers, which is beyond the scope of this text and is covered in real analysis courses.) Call that smallest upper bound \(R\). Since \(S≠{0}\), the number \(R>0\). Therefore, the series converges for all \(x\) such that \(|x|<R,\) and the series falls into case iii.

□

If a series \(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\) falls into case iii. of Note \(\PageIndex{1}\), then the series converges for all \(x\) such that \(|x−a|<R\) for some \(R>0\), and diverges for all \(x\) such that \(|x−a|>R\). The series may converge or diverge at the values \(x\) where \(|x−a|=R\). The set of values \(x\) for which the series \(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\) converges is known as the interval of convergence. Since the series diverges for all values \(x\) where \(|x−a|>R\), the length of the interval is \(2R\), and therefore, the radius of the interval is \(R\). The value \(R\) is called the radius of convergence. For example, since the series \(\displaystyle \sum_{n=0}^∞x^n\) converges for all values \(x\) in the interval \((−1,1)\) and diverges for all values \(x\) such that \(|x|≥1\), the interval of convergence of this series is \((−1,1)\). Since the length of the interval is \(2\), the radius of convergence is \(1\).

Definition: Radius of Convergence

Consider the power series \(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\). The set of real numbers \(x\) where the series converges is the interval of convergence. If there exists a real number \(R>0\) such that the series converges for \(|x−a|<R\) and diverges for \(|x−a|>R,\) then \(R\) is the radius of convergence. If the series converges only at \(x=a\), we say the radius of convergence is \(R=0\). If the series converges for all real numbers \(x\), we say the radius of convergence is \(R=∞\) (Figure \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): For a series \(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\) graph (a) shows a radius of convergence at \(R=0\), graph (b) shows a radius of convergence at \(R=∞\), and graph (c) shows a radius of convergence at \(R\). For graph (c) we note that the series may or may not converge at the endpoints \(x=a+R\) and \(x=a−R\).

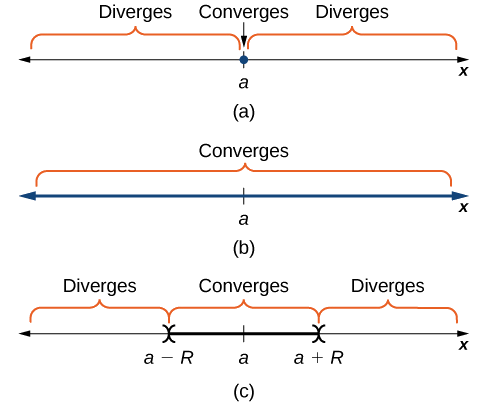
To determine the interval of convergence for a power series, we typically apply the ratio test. In Example \(\PageIndex{1}\), we show the three different possibilities illustrated in Figure \(\PageIndex{1}\).

Example \(\PageIndex{1}\): Finding the Interval and Radius of Convergence

For each of the following series, find the interval and radius of convergence.

1. \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\)
2. \(\displaystyle \sum_{n=0}^∞n!x^n\)
3. \(\displaystyle \sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}\)

Solution

a. To check for convergence, apply the ratio test. We have

\[ \begin{align*} ρ &=\lim_{n→∞} \left|\dfrac{\dfrac{x^{n+1}}{(n+1)!}}{\dfrac{x^n}{n!}}\right| \\[4pt]
&=\lim_{n→∞} \left|\dfrac{x^{n+1}}{(n+1)!}⋅\dfrac{n!}{x^n}\right| \\[4pt]
&=\lim_{n→∞}\left|\dfrac{x^{n+1}}{(n+1)⋅n!}⋅\dfrac{n!}{x^n}\right| \\[4pt]
&=\lim_{n→∞}\left|\dfrac{x}{n+1}\right| \\[4pt]
&=|x|\lim_{n→∞}\dfrac{1}{n+1} \\[4pt]
&=0<1\end{align*}\]

for all values of \(x\). Therefore, the series converges for all real numbers \(x\). The interval of convergence is \((−∞,∞)\) and the radius of convergence is \(R=∞.\)

b. Apply the ratio test. For \(x≠0\), we see that

\[ \begin{align*} ρ &=\lim_{n→∞}\left|\dfrac{(n+1)!x^{n+1}}{n!x^n}\right| \\[4pt]
&=\lim_{n→∞}|(n+1)x| \\[4pt]
&=|x|\lim_{n→∞}(n+1) \\[4pt]
&=∞. \end{align*}\]

Therefore, the series diverges for all \(x≠0\). Since the series is centered at \(x=0\), it must converge there, so the series converges only for \(x≠0\). The interval of convergence is the single value \(x=0\) and the radius of convergence is \(R=0\).

c. In order to apply the ratio test, consider

\[ \begin{align*} ρ &=\lim_{n→∞}\left|\dfrac{\dfrac{(x−2)^{n+1}}{(n+2)3^{n+1}}}{\dfrac{(x−2)^n}{(n+1)3^n}}\right| \\[4pt]
&=\lim_{n→∞} \left|\dfrac{(x−2)^{n+1}}{(n+2)3^{n+1}}⋅\dfrac{(n+1)3^n}{(x−2)^n}\right| \\[4pt]
&=\lim_{n→∞} \left|\dfrac{(x−2)(n+1)}{3(n+2)}\right|\\[4pt]
&=\dfrac{|x−2|}{3}.\end{align*}\]

The ratio \(ρ<1\) if \(|x−2|<3\). Since \(|x−2|<3\) implies that \(−3<x−2<3,\) the series converges absolutely if \(−1<x<5\). The ratio \(ρ>1\) if \(|x−2|>3\). Therefore, the series diverges if \(x<−1\) or \(x>5\). The ratio test is inconclusive if \(ρ=1\). The ratio \(ρ=1\) if and only if \(x=−1\) or \(x=5\). We need to test these values of \(x\) separately. For \(x=−1\), the series is given by

\[ \sum_{n=0}^∞\dfrac{(−1)^n}{n+1}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots . \nonumber \]

Since this is the alternating harmonic series, it converges. Thus, the series converges at \(x=−1\). For \(x=5\), the series is given by

\[ \sum_{n=0}^∞\dfrac{1}{n+1}=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\ldots . \nonumber \]

This is the harmonic series, which is divergent. Therefore, the power series diverges at \(x=5\). We conclude that the interval of convergence is \([−1,5)\) and the radius of convergence is \(R=3\).

Exercise \(\PageIndex{1}\)

Find the interval and radius of convergence for the series

\[ \sum_{n=1}^∞\dfrac{x^n}{\sqrt{n}}. \nonumber \]

Hint

Apply the ratio test to check for absolute convergence.

Answer

The interval of convergence is \([−1,1).\) The radius of convergence is \(R=1.\)

Representing Functions as Power Series

Being able to represent a function by an “infinite polynomial” is a powerful tool. Polynomial functions are the easiest functions to analyze, since they only involve the basic arithmetic operations of addition, subtraction, multiplication, and division. If we can represent a complicated function by an infinite polynomial, we can use the polynomial representation to differentiate or integrate it. In addition, we can use a truncated version of the polynomial expression to approximate values of the function. So, the question is, when can we represent a function by a power series?

Consider again the geometric series

\[1+x+x^2+x^3+\ldots =\sum_{n=0}^∞x^n. \nonumber \]

Recall that the geometric series

\[a+ar+ar^2+ar^3+\ldots \nonumber \]

converges if and only if \(|r|<1.\) In that case, it converges to \(\dfrac{a}{1−r}\). Therefore, if \(|x|<1\), the series in Example \(\PageIndex{1}\) converges to \(\dfrac{1}{1−x}\) and we write

\[1+x+x^2+x^3+\ldots =\dfrac{1}{1−x} \text{ for }|x|<1. \nonumber \]

As a result, we are able to represent the function \(f(x)=\dfrac{1}{1−x}\) by the power series

\[1+x+x^2+x^3+\ldots \text{ when }|x|<1. \nonumber \]

We now show graphically how this series provides a representation for the function \(f(x)=\dfrac{1}{1−x}\) by comparing the graph of \(f\) with the graphs of several of the partial sums of this infinite series.

Example \(\PageIndex{2}\): Graphing a Function and Partial Sums of its Power Series

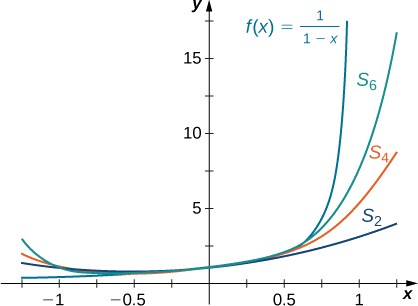
Sketch a graph of \(f(x)=\dfrac{1}{1−x}\) and the graphs of the corresponding partial sums \( \displaystyle S_N(x)=\sum_{n=0}^Nx^n\) for \(N=2,4,6\) on the interval \((−1,1)\). Comment on the approximation \(S_N\) as \(N\) increases.

Solution

From the graph in Figure \(\PageIndex{2}\), you see that as \(N\) increases, \(S_N\) becomes a better approximation for \(f(x)=\dfrac{1}{1−x}\) for \(x\) in the interval \((−1,1)\).

Figure \(\PageIndex{2}\): The graph shows a function and three approximations of it by partial sums of a power series.

Exercise \(\PageIndex{2}\)

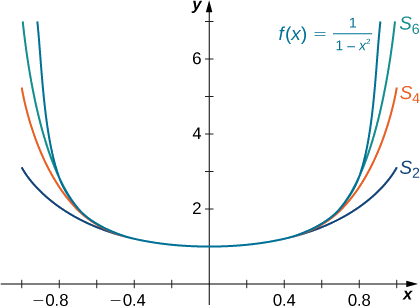
Sketch a graph of \(f(x)=\dfrac{1}{1−x^2}\) and the corresponding partial sums \(\displaystyle S_N(x)=\sum_{n=0}^Nx^{2n}\) for \(N=2,4,6\) on the interval \((−1,1).\)

Hint

\(S_N(x)=1+x^2+\ldots +x^{2N}=\dfrac{1−x^{2(N+1)}}{1−x^2}\)

 

Answer

Next we consider functions involving an expression similar to the sum of a geometric series and show how to represent these functions using power series.

Example \(\PageIndex{3}\): Representing a Function with a Power Series

Use a power series to represent each of the following functions \(f\). Find the interval of convergence.

1. \(f(x)=\dfrac{1}{1+x^3}\)
2. \(f(x)=\dfrac{x^2}{4−x^2}\)

Solution

a. You should recognize this function \(f\) as the sum of a geometric series, because

\[ \dfrac{1}{1+x^3}=\dfrac{1}{1−(−x^3)}. \nonumber \]

Using the fact that, for \(|r|<1,\dfrac{a}{1−r}\) is the sum of the geometric series

\[ \sum_{n=0}^∞ar^n=a+ar+ar^2+\ldots , \nonumber \]

we see that, for \(|−x^3|<1,\)

\[ \begin{align*} \dfrac{1}{1+x^3} &=\dfrac{1}{1−(−x^3)} \\[4pt] &=\sum_{n=0}^∞(−x^3)^n \\[4pt] &=1−x^3+x^6−x^9+\ldots . \end{align*}\]

Since this series converges if and only if \(|−x^3|<1\), the interval of convergence is \((−1,1)\), and we have

\[ \dfrac{1}{1+x^3}=1−x^3+x^6−x^9+\ldots \text{ for }|x|<1.\nonumber \]

b. This function is not in the exact form of a sum of a geometric series. However, with a little algebraic manipulation, we can relate f to a geometric series. By factoring 4 out of the two terms in the denominator, we obtain

\[ \begin{align*} \dfrac{x^2}{4−x^2} &=\dfrac{x^2}{4\left(\dfrac{1−x^2}{4}\right)}\\[4pt] &=\dfrac{x^2}{4\left(1−\left(\dfrac{x}{2}\right)^2\right)}.\end{align*}\]

Therefore, we have

\[ \begin{align*} \dfrac{x^2}{4−x^2} &=\dfrac{x^2}{4\left(1−\left(\dfrac{x}{2}\right)^2\right)} \\[4pt]
&= \dfrac{\dfrac{x^2}{4}}{1−\left(\dfrac{x}{2}\right)^2} \\[4pt]
&= \sum_{n=0}^∞\dfrac{x^2}{4}\left(\dfrac{x}{2}\right)^{2n}. \end{align*}\]

The series converges as long as \(\left|\left(\dfrac{x}{2}\right)^2\right|<1\) (note that when \(\left|\left(\dfrac{x}{2}\right)^2\right|=1\) the series does not converge). Solving this inequality, we conclude that the interval of convergence is \((−2,2)\) and

\[ \begin{align*} \dfrac{x^2}{4−x^2} &=\sum_{n=0}^∞\dfrac{x^{2n+2}}{4^{n+1}}\\[4pt]
&=\dfrac{x^2}{4}+\dfrac{x^4}{4^2}+\dfrac{x^6}{4^3}+ \ldots \end{align*}\]

for \(|x|<2.\)

Exercise \(\PageIndex{3}\)

Represent the function \(f(x)=\dfrac{x^3}{2−x}\) using a power series and find the interval of convergence.

Hint

Rewrite f in the form \(f(x)=\dfrac{g(x)}{1−h(x)}\) for some functions \(g\) and \(h\).

Answer

\(\displaystyle \sum_{n=0}^∞\dfrac{x^{n+3}}{2^{n+1}}\) with interval of convergence \((−2,2)\)

In the remaining sections of this chapter, we will show ways of deriving power series representations for many other functions, and how we can make use of these representations to evaluate, differentiate, and integrate various functions.

Key Concepts

• For a power series centered at \(x=a\), one of the following three properties hold:
  • i. The power series converges only at \(x=a\). In this case, we say that the radius of convergence is \(R=0\).
  • ii. The power series converges for all real numbers \(x\). In this case, we say that the radius of convergence is \(R=∞\).
  • iii. There is a real number R such that the series converges for \(|x−a|<R\) and diverges for \(|x−a|>R\). In this case, the radius of convergence is \(R.\)
• If a power series converges on a finite interval, the series may or may not converge at the endpoints.
• The ratio test may often be used to determine the radius of convergence.
• The geometric series \(\displaystyle \sum_{n=0}^∞x^n=\dfrac{1}{1−x}\) for \(|x|<1\) allows us to represent certain functions using geometric series.

Key Equations

• Power series centered at \(x=0\)

\[ \sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots n\nonumber \]

• Power series centered at \(x=a\)

\[ \sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

Glossary

interval of convergence

the set of real numbers \(x\) for which a power series converges

power series

a series of the form \(\displaystyle \sum_{n=0}^∞c_nx^n\) is a power series centered at \(x=0\); a series of the form \(\displaystyle \sum_{n=0}^∞c_n(x−a)^n\) is a power series centered at \(x=a\)

radius of convergence

if there exists a real number \(R>0\) such that a power series centered at \(x=a\) converges for \(|x−a|<R\) and diverges for \(|x−a|>R\), then \(R\) is the radius of convergence; if the power series only converges at \(x=a\), the radius of convergence is \(R=0\); if the power series converges for all real numbers \(x\), the radius of convergence is \(R=∞\)