10.1E: Exercises for Section 10.1

In exercises 1 - 4, state whether each statement is true, or give an example to show that it is false.

1) If $\displaystyle \sum_{n=1}^∞a_nx^n$ converges, then $a_nx^n→0$ as $n→∞.$

Answer

True. If a series converges then its terms tend to zero.

2) $\displaystyle \sum_{n=1}^∞a_nx^n$ converges at $x=0$ for any real numbers $a_n$.

3) Given any sequence $a_n$, there is always some $R>0$, possibly very small, such that $\displaystyle \sum_{n=1}^∞a_nx^n$ converges on $(−R,R)$.

Answer

False. It would imply that $a_nx^n→0$ for $|x|<R$. If $a_n=n^n$, then $a_nx^n=(nx)^n$ does not tend to zero for any $x≠0$.

4) If $\displaystyle \sum_{n=1}^∞a_nx^n$ has radius of convergence $R>0$ and if $|b_n|≤|a_n|$ for all $n$, then the radius of convergence of $\displaystyle \sum_{n=1}^∞b_nx^n$ is greater than or equal to $R$.

5) Suppose that $\displaystyle \sum_{n=0}^∞a_n(x−3)^n$ converges at $x=6$. At which of the following points must the series also converge? Use the fact that if $\displaystyle \sum a_n(x−c)^n$ converges at $x$, then it converges at any point closer to $c$ than $x$.

a. $x=1$

b. $x=2$

c. $x=3$

d. $x=0$

e. $x=5.99$

f. $x=0.000001$

Answer

It must converge on $(0,6]$ and hence at: a. $x=1$; b. $x=2$; c. $x=3$; d. $x=0$; e. $x=5.99$; and f. $x=0.000001$.

6) Suppose that $\displaystyle \sum_{n=0}^∞a_n(x+1)^n$ converges at $x=−2$. At which of the following points must the series also converge? Use the fact that if $\displaystyle \sum a_n(x−c)^n$ converges at $x$, then it converges at any point closer to $c$ than $x$.

a. $x=2$

b. $x=−1$

c. $x=−3$

d. $x=0$

e. $x=0.99$

f. $x=0.000001$

In the following exercises, suppose that $\left|\dfrac{a_{n+1}}{a_n}\right|→1$ as $n→∞$. Find the radius of convergence for each series.

7) $\displaystyle \sum_{n=0}^∞a_n2^nx^n$

Answer

$\left|\dfrac{a_{n+1}2^{n+1}x^{n+1}}{a_n2^nx^n}\right| =2|x|\left|\dfrac{a_{n+1}}{a_n}\right|→2|x|$ so $R=\frac{1}{2}$

8) $\displaystyle \sum_{n=0}^∞\frac{a_nx^n}{2^n}$

9) $\displaystyle \sum_{n=0}^∞\frac{a_nπ^nx^n}{e^n}$

Answer

$\left|\dfrac{a_{n+1}(\dfrac{π}{e})^{n+1}x^{n+1}}{a_n(\dfrac{π}{e})^nx^n}\right| =\dfrac{π|x|}{e}\left|\dfrac{a_{n+1}}{a_n}\right|→\dfrac{π|x|}{e}$ so $R=\frac{e}{π}$

10) $\displaystyle \sum_{n=0}^∞\frac{a_n(−1)^nx^n}{10^n}$

11) $\displaystyle \sum_{n=0}^∞a_n(−1)^nx^{2n}$

Answer

$\left|\dfrac{a_{n+1}(−1)^{n+1}x^{2n+2}}{a_n(−1)^nx^{2n}}\right| =|x^2|\left|\dfrac{a_{n+1}}{a_n}\right|→|x^2|$ so $R=1$

12) $\displaystyle \sum_{n=0}^∞a_n(−4)^nx^{2n}$

In exercises 13 - 22, find the radius of convergence $R$ and interval of convergence for $\displaystyle \sum a_nx^n$ with the given coefficients $a_n$.

13) $\displaystyle \sum_{n=1}^∞\frac{(2x)^n}{n}$

Answer

$a_n=\dfrac{2^n}{n}$ so $\dfrac{a_{n+1}x}{a_n}→2x$. so $R=\frac{1}{2}$. When $x=\frac{1}{2}$ the series is harmonic and diverges. When $x=−\frac{1}{2}$ the series is alternating harmonic and converges. The interval of convergence is $I=\big[−\frac{1}{2},\frac{1}{2}\big)$.

14) $\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\sqrt{n}}$

15) $\displaystyle \sum_{n=1}^∞\frac{nx^n}{2^n}$

Answer

$a_n=\dfrac{n}{2^n}$ so $\dfrac{a_{n+1}x}{a_n}→\dfrac{x}{2}$ so $R=2$. When $x=±2$ the series diverges by the divergence test. The interval of convergence is $I=(−2,2)$.

16) $\displaystyle \sum_{n=1}^∞\frac{nx^n}{e^n}$

17) $\displaystyle \sum_{n=1}^∞\frac{n^2x^n}{2^n}$

Answer

$a_n=\dfrac{n^2}{2^n}$ so $R=2$. When $x=±2$ the series diverges by the divergence test. The interval of convergence is $I=(−2,2).$

18) $\displaystyle \sum_{k=1}^∞\frac{k^ex^k}{e^k}$

19) $\displaystyle \sum_{k=1}^∞\frac{π^kx^k}{k^π}$

Answer

$a_k=\dfrac{π^k}{k^π}$ so $R=\frac{1}{π}$. When $x=±\frac{1}{π}$ the series is an absolutely convergent $p$-series. The interval of convergence is $I=\left[−\frac{1}{π},\frac{1}{π}\right].$

20) $\displaystyle \sum_{n=1}^∞\frac{x^n}{n!}$

21) $\displaystyle \sum_{n=1}^∞\frac{10^nx^n}{n!}$

Answer

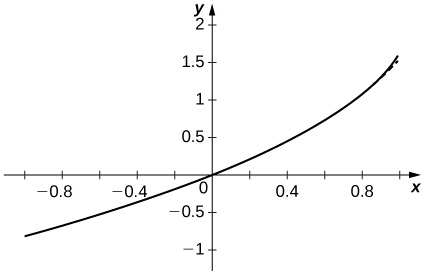
$a_n=\dfrac{10^n}{n!},\dfrac{a_{n+1}x}{a_n}=\dfrac{10x}{n+1}→0<1$ so the series converges for all $x$ by the ratio test and $I=(−∞,∞)$.

22) $\displaystyle \sum_{n=1}^∞(−1)^n\frac{x^n}{\ln(2n)}$

In exercises 23 - 28, find the radius of convergence of each series.

23) $\displaystyle \sum_{k=1}^∞\frac{(k!)^2x^k}{(2k)!}$

Answer

$a_k=\dfrac{(k!)^2}{(2k)!}$ so $\dfrac{a_{k+1}}{a_k}=\dfrac{(k+1)^2}{(2k+2)(2k+1)}→\dfrac{1}{4}$ so $R=4$

24) $\displaystyle \sum_{n=1}^∞\frac{(2n)!x^n}{n^{2n}}$

25) $\displaystyle \sum_{k=1}^∞\frac{k!}{1⋅3⋅5⋯(2k−1)}x^k$

Answer

$a_k=\dfrac{k!}{1⋅3⋅5⋯(2k−1)}$ so $\dfrac{a_{k+1}}{a_k}=\dfrac{k+1}{2k+1}→\dfrac{1}{2}$ so $R=2$

26) $\displaystyle \sum_{k=1}^∞\frac{2⋅4⋅6⋯2k}{(2k)!}x^k$

27) $\displaystyle \sum_{n=1}^∞\frac{x^n}{(^{2n}_n)}$ where $(^n_k)=\dfrac{n!}{k!(n−k)!}$

Answer

$a_n=\dfrac{1}{(^{2n}_n)}$ so $\dfrac{a_{n+1}}{a_n}=\dfrac{\big((n+1)!\big)^2}{(2n+2)!}\dfrac{2n!}{(n!)^2}=\dfrac{(n+1)^2}{(2n+2)(2n+1)}→\dfrac{1}{4}$ so $R=4$

28) $\displaystyle \sum_{n=1}^∞\sin^2nx^n$

In exercises 29 - 32, use the ratio test to determine the radius of convergence of each series.

29) $\displaystyle \sum_{n=1}^∞\frac{(n!)^3}{(3n)!}x^n$

Answer

$\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)^3}{(3n+3)(3n+2)(3n+1)}→\dfrac{1}{27}$ so $R=27$

30) $\displaystyle \sum_{n=1}^∞\frac{2^{3n}(n!)^3}{(3n)!}x^n$

31) $\displaystyle \sum_{n=1}^∞\frac{n!}{n^n}x^n$

Answer

$a_n=\dfrac{n!}{n^n}$ so $\dfrac{a_{n+1}}{a_n}=\dfrac{(n+1)!}{n!}\dfrac{n^n}{(n+1)^{n+1}}=(\dfrac{n}{n+1})^n→\dfrac{1}{e}$ so $R=e$

32) $\displaystyle \sum_{n=1}^∞\frac{(2n)!}{n^{2n}}x^n$

In the following exercises, given that $\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n$ with convergence in $(−1,1)$, find the power series for each function with the given center $a$, and identify its interval of convergence.

33) $f(x)=\dfrac{1}{x};a=1$ (Hint: $\dfrac{1}{x}=\dfrac{1}{1−(1−x)})$

Answer

$\displaystyle f(x)=\sum_{n=0}^∞(1−x)^n$ on $I=(0,2)$

34) $f(x)=\dfrac{1}{1−x^2};a=0$

35) $f(x)=\dfrac{x}{1−x^2};a=0$

Answer

$\displaystyle \sum_{n=0}^∞x^{2n+1}$ on $I=(−1,1)$

36) $f(x)=\dfrac{1}{1+x^2};a=0$

37) $f(x)=\dfrac{x^2}{1+x^2};a=0$

Answer

$\displaystyle \sum_{n=0}^∞(−1)^nx^{2n+2}$ on $I=(−1,1)$

38) $f(x)=\dfrac{1}{2−x};a=1$

39) $f(x)=\dfrac{1}{1−2x};a=0.$

Answer

$\displaystyle \sum_{n=0}^∞2^nx^n$ on $\left(−\frac{1}{2},\frac{1}{2}\right)$

40) $f(x)=\dfrac{1}{1−4x^2};a=0$

41) $f(x)=\dfrac{x^2}{1−4x^2};a=0$

Answer

$\displaystyle \sum_{n=0}^∞4^nx^{2n+2}$ on $\left(−\frac{1}{2},\frac{1}{2}\right)$

42) $f(x)=\dfrac{x^2}{5−4x+x^2};a=2$

Use the result of exercise 43 to find the radius of convergence of the given series in the subsequent exercises (44 - 47).

43) Explain why, if $|a_n|^{1/n}→r>0,$ then $|a_nx^n|^{1/n}→|x|r<1$ whenever $|x|<\frac{1}{r}$ and, therefore, the radius of convergence of $\displaystyle \sum_{n=1}^∞a_nx^n$ is $R=\frac{1}{r}$.

Answer

$|a_nx^n|^{1/n}=|a_n|^{1/n}|x|→|x|r$ as $n→∞$ and $|x|r<1$ when $|x|<\frac{1}{r}$. Therefore, $\displaystyle \sum_{n=1}^∞a_nx^n$ converges when $|x|<\frac{1}{r}$ by the $n^{\text{th}}$ root test.

44) $\displaystyle \sum_{n=1}^∞\frac{x^n}{n^n}$

45) $\displaystyle \sum_{k=1}^∞\left(\frac{k−1}{2k+3}\right)^kx^k$

Answer

$a_k=\left(\dfrac{k−1}{2k+3}\right)^k$ so $(a_k)^{1/k}→\frac{1}{2}<1$ so $R=2$

46) $\displaystyle \sum_{k=1}^∞(\frac{2k^2−1}{k^2+3})^kx^k$

47) $\displaystyle \sum_{n=1}^∞a_n=(n^{1/n}−1)^nx^n$

Answer

$a_n=(n^{1/n}−1)^n$ so $(a_n)^{1/n}→0$ so $R=∞$

48) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ such that $a_n=0$ if $n$ is even. Explain why $p(x)=p(−x).$

49) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ such that $a_n=0$ if $n$ is odd. Explain why $p(x)=−p(−x).$

Answer

We can rewrite $\displaystyle p(x)=\sum_{n=0}^∞a_{2n+1}x^{2n+1}$ and $p(x)=p(−x)$ since $x^{2n+1}=−(−x)^{2n+1}$.

50) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converges on $(−1,1]$. Find the interval of convergence of $p(Ax)$.

51) Suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ converges on $(−1,1]$. Find the interval of convergence of $p(2x−1)$.

Answer

If $x∈[0,1],$ then $y=2x−1∈[−1,1]$ so $\displaystyle p(2x−1)=p(y)=\sum_{n=0}^∞a_ny^n$ converges.

In the following exercises, suppose that $\displaystyle p(x)=\sum_{n=0}^∞a_nx^n$ satisfies $\displaystyle \lim_{n→∞}\frac{a_{n+1}}{a_n}=1$ where $a_n≥0$ for each $n$. State whether each series converges on the full interval $(−1,1)$, or if there is not enough information to draw a conclusion. Use the comparison test when appropriate.

52) $\displaystyle \sum_{n=0}^∞a_nx^{2n}$

53) $\displaystyle \sum_{n=0}^∞a_{2n}x^{2n}$

Answer

Converges on $(−1,1)$ by the ratio test

54) $\displaystyle \sum_{n=0}^∞a_{2n}x^n$ (Hint:$x=±\sqrt{x^2}$)

55) $\displaystyle \sum_{n=0}^∞a_{n^2}x^{n^2}$ (Hint: Let $b_k=a_k$ if $k=n^2$ for some $n$, otherwise $b_k=0$.)

Answer

Consider the series $\displaystyle \sum b_kx^k$ where $b_k=a_k$ if $k=n^2$ and $b_k=0$ otherwise. Then $b_k≤a_k$ and so the series converges on $(−1,1)$ by the comparison test.

56) Suppose that $p(x)$ is a polynomial of degree $N$. Find the radius and interval of convergence of $\displaystyle \sum_{n=1}^∞p(n)x^n$.

57) [T] Plot the graphs of $\dfrac{1}{1−x}$ and of the partial sums $\displaystyle S_N=\sum_{n=0}^Nx^n$ for $n=10,20,30$ on the interval $[−0.99,0.99]$. Comment on the approximation of $\dfrac{1}{1−x}$ by $S_N$ near $x=−1$ and near $x=1$ as $N$ increases.

Answer

The approximation is more accurate near $x=−1$. The partial sums follow $\dfrac{1}{1−x}$ more closely as $N$ increases but are never accurate near $x=1$ since the series diverges there.

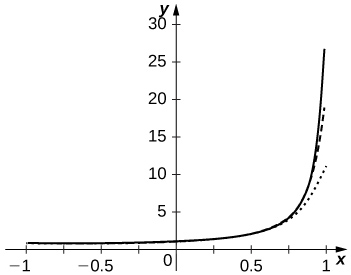
58) [T] Plot the graphs of $−\ln(1−x)$ and of the partial sums $\displaystyle S_N=\sum_{n=1}^N\frac{x^n}{n}$ for $n=10,50,100$ on the interval $[−0.99,0.99]$. Comment on the behavior of the sums near $x=−1$ and near $x=1$ as $N$ increases.

59) [T] Plot the graphs of the partial sums $\displaystyle S_n=\sum_{n=1}^N\frac{x^n}{n^2}$ for $n=10,50,100$ on the interval $[−0.99,0.99]$. Comment on the behavior of the sums near $x=−1$ and near $x=1$ as $N$ increases.

Answer

The approximation appears to stabilize quickly near both $x=±1$.

60) [T] Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=1}^N(\sin n) x^n$ for $n=10,50,100$ on the interval $[−0.99,0.99]$. Comment on the behavior of the sums near $x=−1$ and near $x=1$ as $N$ increases.

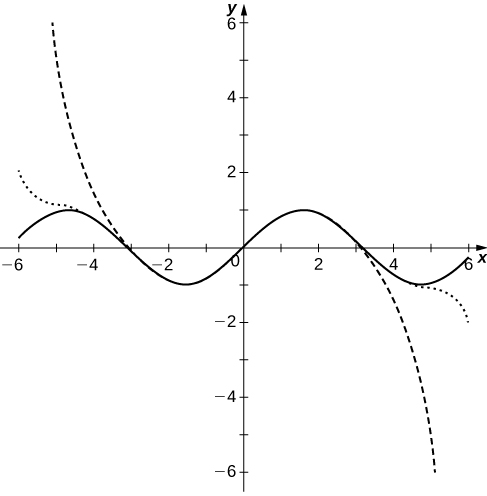
61) [T] Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n+1}}{(2n+1)!}$ for $n=3,5,10$ on the interval $[−2π,2π]$. Comment on how these plots approximate $\sin x$ as $N$ increases.

Answer

The polynomial curves have roots close to those of $\sin x$ up to their degree and then the polynomials diverge from $\sin x$.

62) [T] Plot the graphs of the partial sums $\displaystyle S_N=\sum_{n=0}^N(−1)^n\frac{x^{2n}}{(2n)!}$ for $n=3,5,10$ on the interval $[−2π,2π]$. Comment on how these plots approximate $\cos x$ as $N$ increases.

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.