10.4: Working with Taylor Series
- Page ID
- 2572
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Write the terms of the binomial series.
- Recognize the Taylor series expansions of common functions.
- Recognize and apply techniques to find the Taylor series for a function.
- Use Taylor series to solve differential equations.
- Use Taylor series to evaluate non-elementary integrals.
In the preceding section, we defined Taylor series and showed how to find the Taylor series for several common functions by explicitly calculating the coefficients of the Taylor polynomials. In this section we show how to use those Taylor series to derive Taylor series for other functions. We then present two common applications of power series. First, we show how power series can be used to solve differential equations. Second, we show how power series can be used to evaluate integrals when the antiderivative of the integrand cannot be expressed in terms of elementary functions. In one example, we consider \(\displaystyle \int e^{−x^2}dx,\) an integral that arises frequently in probability theory.
The Binomial Series
Our first goal in this section is to determine the Maclaurin series for the function \( f(x)=(1+x)^r\) for all real numbers \( r\). The Maclaurin series for this function is known as the binomial series. We begin by considering the simplest case: \( r\) is a nonnegative integer. We recall that, for \( r=0,\,1,\,2,\,3,\,4,\;f(x)=(1+x)^r\) can be written as
\[\begin{align*} f(x) &=(1+x)^0=1, \\[4pt] f(x) &=(1+x)^1=1+x, \\[4pt] f(x) &=(1+x)^2=1+2x+x^2, \\[4pt] f(x) &=(1+x)^3=1+3x+3x^2+x^3 \\[4pt] f(x) &=(1+x)^4=1+4x+6x^2+4x^3+x^4. \end{align*}\]
The expressions on the right-hand side are known as binomial expansions and the coefficients are known as binomial coefficients. More generally, for any nonnegative integer \( r\), the binomial coefficient of \( x^n\) in the binomial expansion of \( (1+x)^r\) is given by
\[\binom{r}{n}=\dfrac{r!}{n!(r−n)!}\label{eq6.6} \]
and
\[\begin{align} f(x)&=(1+x)^r\nonumber\\[5pt]
&= \binom{r}{0}+\binom{r}{1}x+\binom{r}{2}x^2+\binom{r}{3}x^3+⋯+\binom{r}{r-1}x^{r−1}+\binom{r}{r}x^r \nonumber\\[5pt]
&=\sum_{n=0}^r\binom{r}{n}x^n.\label{eq6.7}\end{align} \]
For example, using this formula for \( r=5\), we see that
\[ \begin{align*} f(x) &=(1+x)^5 \\[4pt] &=\binom{5}{0}1+\binom{5}{1}x+\binom{5}{2}x^2+\binom{5}{3}x^3+\binom{5}{4}x^4+\binom{5}{5}x^5 \\[4pt] &=\dfrac{5!}{0!5!}1+\dfrac{5!}{1!4!}x+\dfrac{5!}{2!3!}x^2+\dfrac{5!}{3!2!}x^3+\dfrac{5!}{4!1!}x^4+\dfrac{5!}{5!0!}x^5 \\[4pt] &=1+5x+10x^2+10x^3+5x^4+x^5. \end{align*}\]
We now consider the case when the exponent \(r\) is any real number, not necessarily a nonnegative integer. If \(r\) is not a nonnegative integer, then \(f(x)=(1+x)^r\) cannot be written as a finite polynomial. However, we can find a power series for \(f\). Specifically, we look for the Maclaurin series for \(f\). To do this, we find the derivatives of \(f\) and evaluate them at \(x=0\).
\[ \begin{align*} f(x) &=(1+x)^r & f(0) &=1 \\[4pt] f′(x) &=r(1+x)^{r−1} & f'(0) &=r \\[4pt] f''(x) &=r(r−1)(1+x)^{r−2} & f''(0) &=r(r−1) \\[4pt] f'''(x) &=r(r−1)(r−2)(1+x)^{r−3} & f'''(0) &=r(r−1)(r−2) \\[4pt] f^{(n)}(x) &=r(r−1)(r−2)⋯(r−n+1)(1+x)^{r−n} & f^{(n)}(0) &=r(r−1)(r−2)⋯(r−n+1) \end{align*}\]
We conclude that the coefficients in the binomial series are given by
\[\dfrac{f^{(n)}(0)}{n!}=\dfrac{r(r−1)(r−2)⋯(r−n+1)}{n!}.\label{eq6.8} \]
We note that if \(r\) is a nonnegative integer, then the \((r+1)^{\text{st}}\) derivative \( f^{(r+1)}\) is the zero function, and the series terminates. In addition, if \( r\) is a nonnegative integer, then Equation \ref{eq6.8} for the coefficients agrees with Equation \ref{eq6.6} for the coefficients, and the formula for the binomial series agrees with Equation \ref{eq6.7} for the finite binomial expansion. More generally, to denote the binomial coefficients for any real number \( r\), we define
\[\binom{r}{n}=\dfrac{(r−1)(r−2)⋯(r−n+1)}{n!}. \nonumber \]
With this notation, we can write the binomial series for \( (1+x)^r\) as
\[\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯. \label{bin1} \]
We now need to determine the interval of convergence for the binomial series Equation \ref{bin1}. We apply the ratio test. Consequently, we consider
\[\begin{align*} \dfrac{|a_{n+1}|}{|a_n|} &=\dfrac{|r(r−1)(r−2)⋯(r−n)|x||^{n+1}}{(n+1)!}⋅\dfrac{n!}{|r(r−1)(r−2)⋯(r−n+1)||x|^n} \\[4pt] &=\dfrac{|r−n||x|}{|n+1|} \end{align*}\].
Since
\[\lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=|x|<1 \nonumber \]
if and only if \( |x|<1\), we conclude that the interval of convergence for the binomial series is \( (−1,1)\). The behavior at the endpoints depends on \( r\). It can be shown that for \( r≥0\) the series converges at both endpoints; for \( −1<r<0\), the series converges at \( x=1\) and diverges at \( x=−1\); and for \( r<−1\), the series diverges at both endpoints. The binomial series does converge to \( (1+x)^r\) in \( (−1,1)\) for all real numbers \( r\), but proving this fact by showing that the remainder \( R_n(x)→0\) is difficult.
For any real number \( r\), the Maclaurin series for \( f(x)=(1+x)^r\) is the binomial series. It converges to \( f\) for \( |x|<1\), and we write
\[(1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+r\dfrac{(r−1)⋯(r−n+1)}{n!}x^n+⋯ \nonumber \]
for \( |x|<1\).
We can use this definition to find the binomial series for \( f(x)=\sqrt{1+x}\) and use the series to approximate \( \sqrt{1.5}\).
- Find the binomial series for \( f(x)=\sqrt{1+x}\).
- Use the third-order Maclaurin polynomial \( p_3(x)\) to estimate \( \sqrt{1.5}\). Use Taylor’s theorem to bound the error. Use a graphing utility to compare the graphs of \( f\) and \( p_3\).
Solution
a. Here \( r=\dfrac{1}{2}\). Using the definition for the binomial series, we obtain
\( \qquad \) \(\begin{align*} \sqrt{1+x} &=1+\dfrac{1}{2}x+\dfrac{(1/2)(−1/2)}{2!}x^2+\dfrac{(1/2)(−1/2)(−3/2)}{3!}x^3+⋯\\[5pt]
&=1+\dfrac{1}{2}x−\dfrac{1}{2!}\dfrac{1}{2^2}x^2+\dfrac{1}{3!}\dfrac{1⋅3}{2^3}x^3−⋯+\dfrac{(−1)^{n+1}}{n!}\dfrac{1⋅3⋅5⋯(2n−3)}{2^n}x^n+⋯\\[5pt]
&=1+\dfrac{1}{2}x+\sum_{n=2}^∞\dfrac{(−1)^{n+1}}{n!}\dfrac{1⋅3⋅5⋯(2n−3)}{2^n}x^n. \end{align*}\)
b. From the result in part a. the third-order Maclaurin polynomial is
\( p_3(x)=1+\dfrac{1}{2}x−\dfrac{1}{8}x^2+\dfrac{1}{16}x^3\).
Therefore,
\( \sqrt{1.5}=\sqrt{1+0.5}≈1+\dfrac{1}{2}(0.5)−\dfrac{1}{8}(0.5)^2+\dfrac{1}{16}(0.5)^3≈1.2266.\)
From Taylor’s theorem, the error satisfies
\( R_3(0.5)=\dfrac{f^{(4)}(c)}{4!}(0.5)^4\)
for some \( c\) between \( 0\) and \( 0.5\). Since \( f^{(4)}(x)=−\dfrac{15}{2^4(1+x)^{7/2}}\), and the maximum value of \( ∣f^{(4)}(x)∣\) on the interval \( (0,0.5)\) occurs at \( x=0\), we have
\( |R_3(0.5)|≤\dfrac{15}{4!2^4}(0.5)^4≈0.00244.\)
The function and the Maclaurin polynomial \( p_3\) are graphed in Figure \(\PageIndex{1}\).
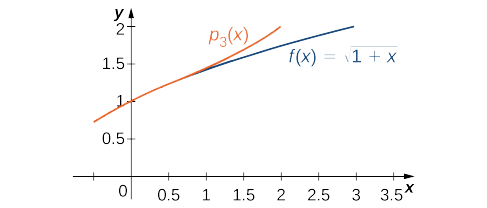
Find the binomial series for \( f(x)=\dfrac{1}{(1+x)^2}\).
- Hint
-
Use the definition of binomial series for \( r=−2\).
- Answer
-
\(\displaystyle \sum_{n=0}^∞(−1)^n(n+1)x^n\)
Common Functions Expressed as Taylor Series
At this point, we have derived Maclaurin series for exponential, trigonometric, and logarithmic functions, as well as functions of the form \( f(x)=(1+x)^r\). In Table \(\PageIndex{1}\), we summarize the results of these series. We remark that the convergence of the Maclaurin series for \( f(x)=\ln(1+x)\) at the endpoint \( x=1\) and the Maclaurin series for \( f(x)=\tan^{−1}x\) at the endpoints \( x=1\) and \( x=−1\) relies on a more advanced theorem than we present here. (Refer to Abel’s theorem for a discussion of this more technical point.)
| Function | Maclaurin Series | Interval of Convergence |
|---|---|---|
| \( f(x)=\dfrac{1}{1−x}\) | \(\displaystyle \sum_{n=0}^∞x^n\) | \( −1<x<1\) |
| \( f(x)=e^x\) | \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\) | \( −∞<x<∞\) |
| \( f(x)=\sin x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\) | \( −∞<x<∞\) |
| \( f(x)=\cos x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{(2n)!}\) | \( −∞<x<∞\) |
| \( f(x)=\ln(1+x)\) | \(\displaystyle \sum_{n=0}^∞(−1)^{n+1}\dfrac{x^n}{n}\) | \( −1<x \le 1\) |
| \( f(x)=\tan^{−1}x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{2n+1}\) | \( −1 \le x \le 1\) |
| \( f(x)=(1+x)^r\) | \(\displaystyle \sum_{n=0}^∞\binom{r}{n}x^n\) | \( −1<x<1\) Convergence at the endpoints depends on the value of \(r\) |
Earlier in the chapter, we showed how you could combine power series to create new power series. Here we use these properties, combined with the Maclaurin series in Table \(\PageIndex{1}\), to create Maclaurin series for other functions.
Find the Maclaurin series of each of the following functions by using one of the series listed in Table \(\PageIndex{1}\).
- \( f(x)=\cos\sqrt{x}\)
- \( f(x)=\sinh x\)
Solution
a. Using the Maclaurin series for \( \cos x\) we find that the Maclaurin series for \( \cos\sqrt{x}\) is given by
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^n(\sqrt{x})^{2n}}{(2n)!}=\sum_{n=0}^∞\dfrac{(−1)^nx^n}{(2n)!}=1−\dfrac{x}{2!}+\dfrac{x^2}{4!}−\dfrac{x^3}{6!}+\dfrac{x^4}{8!}−⋯.\)
This series converges to \( \cos\sqrt{x}\) for all \( x\) in the domain of \( \cos\sqrt{x}\); that is, for all \( x≥0\).
b. To find the Maclaurin series for \( \sinh x,\) we use the fact that
\( \sinh x=\dfrac{e^x−e^{−x}}{2}.\)
Using the Maclaurin series for \( e^x\), we see that the \(n^{\text{th}}\) term in the Maclaurin series for \(\sinh x\) is given by
\( \dfrac{x^n}{n!}−\dfrac{(−x)^n}{n!}.\)
For \( n\) even, this term is zero. For \( n\) odd, this term is \( \dfrac{2x^n}{n!}\). Therefore, the Maclaurin series for \(\sinh x\) has only odd-order terms and is given by
\(\displaystyle \sum_{n=0}^∞\dfrac{x^{2n+1}}{(2n+1)!}=x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+⋯.\)
Find the Maclaurin series for \( \sin(x^2).\)
- Hint
-
Use the Maclaurin series for \( \sin x.\)
- Answer
-
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{4n+2}}{(2n+1)!}\)
We also showed previously in this chapter how power series can be differentiated term by term to create a new power series. In Example \(\PageIndex{3}\), we differentiate the binomial series for \( \sqrt{1+x}\) term by term to find the binomial series for \( \dfrac{1}{\sqrt{1+x}}\). Note that we could construct the binomial series for \( \dfrac{1}{\sqrt{1+x}}\) directly from the definition, but differentiating the binomial series for \( \sqrt{1+x}\) is an easier calculation.
Use the binomial series for \( \sqrt{1+x}\) to find the binomial series for \( \dfrac{1}{\sqrt{1+x}}\).
Solution
The two functions are related by
\( \dfrac{d}{dx}\sqrt{1+x}=\dfrac{1}{2\sqrt{1+x}}\),
so the binomial series for \( \dfrac{1}{\sqrt{1+x}}\) is given by
\(\displaystyle \dfrac{1}{\sqrt{1+x}}=2\dfrac{d}{dx}\sqrt{1+x}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n.\)
Find the binomial series for \( f(x)=\dfrac{1}{(1+x)^{3/2}}\)
- Hint
-
Differentiate the series for \( \dfrac{1}{\sqrt{1+x}}\)
- Answer
-
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n+1)}{2^n}x^n\)
In this example, we differentiated a known Taylor series to construct a Taylor series for another function. The ability to differentiate power series term by term makes them a powerful tool for solving differential equations. We now show how this is accomplished.
Solving Differential Equations with Power Series
Consider the differential equation
\[y′(x)=y.\nonumber \]
Recall that this is a first-order separable equation and its solution is \(y=Ce^x\). This equation is easily solved using techniques discussed earlier in the text. For most differential equations, however, we do not yet have analytical tools to solve them. Power series are an extremely useful tool for solving many types of differential equations. In this technique, we look for a solution of the form \(\displaystyle y=\sum_{n=0}^∞c_nx^n\) and determine what the coefficients would need to be. In the next example, we consider an initial-value problem involving \(y′=y\) to illustrate the technique.
Use power series to solve the initial-value problem \(y′=y,\quad y(0)=3.\)
Solution
Suppose that there exists a power series solution
\(\displaystyle y(x)=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯.\)
Differentiating this series term by term, we obtain
\( y′=c_1+2c_2x+3c_3x^2+4c_4x^3+⋯.\)
If \(y\) satisfies the differential equation, then
\( c_0+c_1x+c_2x^2+c_3x^3+⋯=c_1+2c_2x+3c_3x^2+4c_3x^3+⋯.\)
Using the uniqueness of power series representations, we know that these series can only be equal if their coefficients are equal. Therefore,
\( c_0=c_1,\)
\( c_1=2c_2,\)
\( c_2=3c_3,\)
\( c_3=4c_4,\)
⋮
Using the initial condition \( y(0)=3\) combined with the power series representation
\( y(x)=c_0+c_1x+c_2x^2+c_3x^3+⋯\),
we find that \( c_0=3\). We are now ready to solve for the rest of the coefficients. Using the fact that \( c_0=3\), we have
\[\begin{align*} c_1&=c_0=3=\dfrac{3}{1!},\\[5pt]
c_2&=\dfrac{c_1}{2}=\dfrac{3}{2}=\dfrac{3}{2!},\\[5pt]
c_3&=\dfrac{c_2}{3}=\dfrac{3}{3⋅2}=\dfrac{3}{3!},\\[5pt]
c_4&=\dfrac{c_3}{4}=\dfrac{3}{4⋅3⋅2}=\dfrac{3}{4!}.\end{align*}\]
Therefore,
\[y=3\left[1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3\dfrac{1}{4!}x^4+⋯\right]=3\sum_{n=0}^∞\dfrac{x^n}{n!}.\nonumber \]
You might recognize
\[\sum_{n=0}^∞\dfrac{x^n}{n!}\nonumber \]
as the Taylor series for \( e^x\). Therefore, the solution is \( y=3e^x\).
Use power series to solve \( y′=2y,\quad y(0)=5.\)
- Hint
-
The equations for the first several coefficients \( c_n\) will satisfy \( c_0=2c_1,\,c_1=2⋅2c_2,\,c_2=2⋅3c_3,\,….\) In general, for all \( n≥0,\;c_n=2(n+1)C_{n+1}\).
- Answer
-
\( y=5e^{2x}\)
We now consider an example involving a differential equation that we cannot solve using previously discussed methods. This differential equation
\[y''−xy=0\nonumber \]
is known as Airy’s equation. It has many applications in mathematical physics, such as modeling the diffraction of light. Here we show how to solve it using power series.
Use power series to solve \(y''−xy=0\) with the initial conditions \( y(0)=a\) and \( y'(0)=b.\)
Solution
We look for a solution of the form
\[y=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯\nonumber \]
Differentiating this function term by term, we obtain
\[\begin{align*} y′&=c_1+2c_2x+3c_3x^2+4c_4x^3+⋯,\\[4pt]
y''&=2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+⋯.\end{align*}\]
If \(y\) satisfies the equation \( y''=xy\), then
\( 2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+⋯=x(c_0+c_1x+c_2x^2+c_3x^3+⋯).\)
Using the Uniqueness of Power Series Theorem (from an earlier Section) on the uniqueness of power series representations, we know that coefficients of the same degree must be equal. Therefore,
\( 2⋅1c_2=0,\)
\( 3⋅2c_3=c_0,\)
\( 4⋅3c_4=c_1,\)
\( 5⋅4c_5=c_2,\)
⋮
More generally, for \( n≥3\), we have \( n⋅(n−1)c_n=c_{n−3}\). In fact, all coefficients can be written in terms of \( c_0\) and \( c_1\). To see this, first note that \( c_2=0\). Then
\( c_3=\dfrac{c_0}{3⋅2}\),
\( c_4=\dfrac{c_1}{4⋅3}\).
For \( c_5,\,c_6,\,c_7\), we see that
\[\begin{align*} c_5&=\dfrac{c_2}{5⋅4}=0,\\[5pt]
c_6&=\dfrac{c_3}{6⋅5}=\dfrac{c_0}{6⋅5⋅3⋅2},\\[5pt]
c_7&=\dfrac{c_4}{7⋅6}=\dfrac{c_1}{7⋅6⋅4⋅3}.\end{align*}\]
Therefore, the series solution of the differential equation is given by
\( y=c_0+c_1x+0⋅x^2+\dfrac{c_0}{3⋅2}x^3+\dfrac{c_1}{4⋅3}x^4+0⋅x^5+\dfrac{c_0}{6⋅5⋅3⋅2}x^6+\dfrac{c_1}{7⋅6⋅4⋅3}x^7+⋯.\)
The initial condition \( y(0)=a\) implies \( c_0=a\). Differentiating this series term by term and using the fact that \( y′(0)=b\), we conclude that \( c_1=b\).
Therefore, the solution of this initial-value problem is
\( y=a\left(1+\dfrac{x^3}{3⋅2}+\dfrac{x^6}{6⋅5⋅3⋅2}+⋯\right)+b\left(x+\dfrac{x^4}{4⋅3}+\dfrac{x^7}{7⋅6⋅4⋅3}+⋯\right).\)
Use power series to solve \( y''+x^2y=0\) with the initial condition \( y(0)=a\) and \( y′(0)=b\).
- Hint
-
The coefficients satisfy \( c_0=a,\,c_1=b,\,c_2=0,\,c_3=0,\) and for \( n≥4,\; n(n−1)c_n=−c_{n−4}\).
- Answer
-
\(y=a\left(1−\dfrac{x^4}{3⋅4}+\dfrac{x^8}{3⋅4⋅7⋅8}−⋯\right)+b\left(x−\dfrac{x^5}{4⋅5}+\dfrac{x^9}{4⋅5⋅8⋅9}−⋯\right)\)
Evaluating Non-elementary Integrals
Solving differential equations is one common application of power series. We now turn to a second application. We show how power series can be used to evaluate integrals involving functions whose antiderivatives cannot be expressed using elementary functions.
One integral that arises often in applications in probability theory is \(\displaystyle \int e^{−x^2}\,dx.\) Unfortunately, the antiderivative of the integrand \( e^{−x^2}\) is not an elementary function. By elementary function, we mean a function that can be written using a finite number of algebraic combinations or compositions of exponential, logarithmic, trigonometric, or power functions. We remark that the term “elementary function” is not synonymous with noncomplicated function. For example, the function \( f(x)=\sqrt{x^2−3x}+e^{x^3}−\sin(5x+4)\) is an elementary function, although not a particularly simple-looking function. Any integral of the form \(\displaystyle \int f(x)\,dx\) where the antiderivative of \( f\) cannot be written as an elementary function is considered a non-elementary integral.
Non-elementary integrals cannot be evaluated using the basic integration techniques discussed earlier. One way to evaluate such integrals is by expressing the integrand as a power series and integrating term by term. We demonstrate this technique by considering \(\displaystyle \int e^{−x^2}\,dx.\)
- Express \(\displaystyle \int e^{−x^2}dx\) as an infinite series.
- Evaluate \(\displaystyle \int ^1_0e^{−x^2}dx\) to within an error of \( 0.01\).
Solution
a. The Maclaurin series for \( e^{−x^2}\) is given by
\[\begin{align*} e^{−x^2}&=\sum_{n=0}^∞\dfrac{(−x^2)^n}{n!}\\[5pt]
&=1−x^2+\dfrac{x^4}{2!}−\dfrac{x^6}{3!}+⋯+(−1)^n\dfrac{x^{2n}}{n!}+⋯\\[5pt]
&=\sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{n!}.\end{align*}\]
Therefore,
\[\begin{align*} \int e^{−x^2}\,dx&=\int \left(1−x^2+\dfrac{x^4}{2!}−\dfrac{x^6}{3!}+⋯+(−1)^n\dfrac{x^{2n}}{n!}+⋯\right)\,dx\\[5pt]
&=C+x−\dfrac{x^3}{3}+\dfrac{x^5}{5.2!}−\dfrac{x^7}{7.3!}+⋯+(−1)^n\dfrac{x^{2n+1}}{(2n+1)n!}+⋯.\end{align*}\]
b. Using the result from part a. we have
\[ \int ^1_0e^{−x^2}\,dx=1−\dfrac{1}{3}+\dfrac{1}{10}−\dfrac{1}{42}+\dfrac{1}{216}−⋯.\nonumber \]
The sum of the first four terms is approximately \( 0.74\). By the alternating series test, this estimate is accurate to within an error of less than \( \dfrac{1}{216}≈0.0046296<0.01.\)
Express \(\displaystyle \int \cos\sqrt{x}\,dx\) as an infinite series. Evaluate \(\displaystyle \int ^1_0\cos\sqrt{x}\,dx\) to within an error of \( 0.01\).
- Hint
-
Use the series found in Example \(\PageIndex{2}\).
- Answer
-
\(\displaystyle C+\sum_{n=1}^∞(−1)^{n+1}\dfrac{x^n}{n(2n−2)!}\) The definite integral is approximately \( 0.764\) to within an error of \( 0.01\).
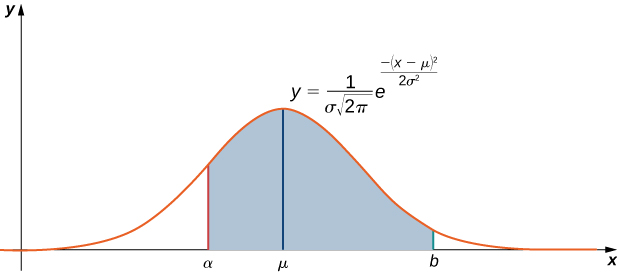
As mentioned above, the integral \(\displaystyle \int e^{−x^2}\,dx\) arises often in probability theory. Specifically, it is used when studying data sets that are normally distributed, meaning the data values lie under a bell-shaped curve. For example, if a set of data values is normally distributed with mean \( μ\) and standard deviation \( σ\), then the probability that a randomly chosen value lies between \( x=a\) and \( x=b\) is given by
\[\dfrac{1}{σ\sqrt{2π}}\int ^b_ae^{−(x−μ)^2/(2σ^2)}\,dx.\label{probeq} \]
(See Figure \(\PageIndex{2}\).)
To simplify this integral, we typically let \( z=\dfrac{x−μ}{σ}\). This quantity \(z\) is known as the \(z\) score of a data value. With this simplification, integral Equation \ref{probeq} becomes
\[\dfrac{1}{\sqrt{2π}}\int ^{(b−μ)/σ}_{(a−μ)/σ}e^{−z^2/2}\,dz. \nonumber \]
In Example \(\PageIndex{7}\), we show how we can use this integral in calculating probabilities.
Suppose a set of standardized test scores are normally distributed with mean \( μ=100\) and standard deviation \( σ=50\). Use Equation \ref{probeq} and the first six terms in the Maclaurin series for \( e^{−x^2/2}\) to approximate the probability that a randomly selected test score is between \( x=100\) and \( x=200\). Use the alternating series test to determine how accurate your approximation is.
Solution
Since \( μ=100,σ=50,\) and we are trying to determine the area under the curve from \( a=100\) to \( b=200\), integral Equation \ref{probeq} becomes
\[ \dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz.\label{probeqEx7} \]
The Maclaurin series for \( e^{−x^2/2}\) is given by
\[ \begin{align*} e^{−x^2/2}&=\sum_{n=0}^∞\dfrac{\left(−\dfrac{x^2}{2}\right)^n}{n!}\\[5pt]
&=1−\dfrac{x^2}{2^1⋅1!}+\dfrac{x^4}{2^2⋅2!}−\dfrac{x^6}{2^3⋅3!}+⋯+(−1)^n\dfrac{x^{2n}}{2^n⋅n}!+⋯\\[5pt]
&=\sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{2^n⋅n!}.\end{align*}\]
Therefore,
\[\begin{align*} \dfrac{1}{\sqrt{2π}}\int e^{−z^2/2}\,dz&=\dfrac{1}{\sqrt{2π}}\int \left(1−\dfrac{z^2}{2^1⋅1!}+\dfrac{z^4}{2^2⋅2!}−\dfrac{z^6}{2^3⋅3!}+⋯+(−1)^n\dfrac{z^{2n}}{2^n⋅n!}+⋯\right)dz\\[5pt]
&=\dfrac{1}{\sqrt{2π}}\left(C+z−\dfrac{z^3}{3⋅2^1⋅1!}+\dfrac{z^5}{5⋅2^2⋅2!}−\dfrac{z^7}{7⋅2^3⋅3!}+⋯+(−1)^n\dfrac{z^{2n+1}}{(2n+1)2^n⋅n!}+⋯\right)\end{align*}\]
We now use this result to evaluate the definite integral from Equation \ref{probeqEx7}:
\[\dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz=\dfrac{1}{\sqrt{2π}}\left(2−\dfrac{8}{6}+\dfrac{32}{40}−\dfrac{128}{336}+\dfrac{512}{3456}−\dfrac{2^{11}}{11⋅2^5⋅5!}+⋯\right)\nonumber \]
Using the first five terms, we estimate that the probability is approximately 0.4729. By the alternating series test, we see that this estimate is accurate to within
\[ \dfrac{1}{\sqrt{2π}}\dfrac{2^{13}}{13⋅2^6⋅6!}≈0.00546.\nonumber \]
Analysis
If you are familiar with probability theory, you may know that the probability that a data value is within two standard deviations of the mean is approximately \( 95\%.\) Here we calculated the probability that a data value is between the mean and two standard deviations above the mean, so the estimate should be around \( 47.5\%\). The estimate, combined with the bound on the accuracy, falls within this range.
Alternative method. If term-by-term integration is done instead, the result of evaluating the definite integral is
\(\displaystyle \ \dfrac{1}{\sqrt{2π}} \sum_{n=0}^∞\dfrac{ (-1)^n}{2^n n!} \int ^2_0 z^{2n}\; dz =\displaystyle \ \dfrac{1}{\sqrt{2π}} \sum_{n=0}^∞\dfrac{ (-1)^n}{(2n+1)2^n n!} \left[ 2^{2n+1}-0^{2n+1} \right] =\displaystyle \ \dfrac{1}{\sqrt{2π}} \sum_{n=0}^∞\dfrac{ (-1)^n 2^{n+1}}{ n!(2n+1)} \)
\(=\dfrac{1}{\sqrt{2π}}\left(\dfrac{2}{1\cdot 0! }−\dfrac{4}{3 \cdot 1! }+\dfrac{8}{5 \cdot 2! }−\dfrac{16}{7 \cdot 3!}+\dfrac{32}{ 9 \cdot 4!}−\dfrac{64}{11 \cdot 5! }+⋯\right) \)
\(=\dfrac{1}{\sqrt{2π}}\left(2−\dfrac{4}{3}+\dfrac{4}{5}−\dfrac{8}{21}+\dfrac{4}{27}−\dfrac{8}{165}+⋯\right) \)
Given a set of normally distributed standardized test scores with mean \( μ=100\) and standard deviation \( σ=50\), use the first five terms of the Maclaurin series for \( e^{−x^2/2}\) to estimate the probability that a randomly selected test score is between \( 100\) and \( 150\). Use the alternating series test to determine the accuracy of this estimate.
- Hint
-
Evaluate \(\displaystyle \int ^1_0e^{−z^2/2}\,dz\) using the first five terms of the Maclaurin series for \( e^{−z^2/2}\).
- Answer
-
The estimate is approximately \( 0.3414.\) This estimate is accurate to within \( 0.0000094.\)
Another application in which a non-elementary integral arises involves the period of a pendulum. The integral is
\[\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \].
An integral of this form is known as an elliptic integral of the first kind. Elliptic integrals originally arose when trying to calculate the arc length of an ellipse. We now show how to use power series to approximate this integral.
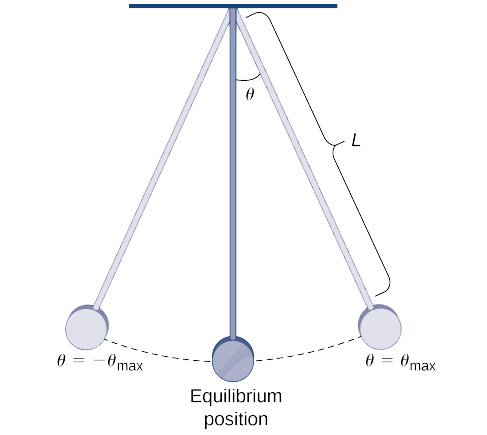
The period of a pendulum is the time it takes for a pendulum to make one complete back-and-forth swing. For a pendulum with length \( L\) that makes a maximum angle \( θ_{max}\) with the vertical, its period \( T\) is given by
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \]
where \( g\) is the acceleration due to gravity and \( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) (see Figure \(\PageIndex{3}\)). (We note that this formula for the period arises from a non-linearized model of a pendulum. In some cases, for simplification, a linearized model is used and \(\sin θ\) is approximated by \( θ\).)
Use the binomial series
\[ \dfrac{1}{\sqrt{1+x}}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\nonumber \]
to estimate the period of this pendulum. Specifically, approximate the period of the pendulum if
- you use only the first term in the binomial series, and
- you use the first two terms in the binomial series.
Solution
We use the binomial series, replacing x with \( −k^2\sin^2θ.\) Then we can write the period as
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
a. Using just the first term in the integrand, the first-order estimate is
\[ T≈4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\,dθ=2π\sqrt{\dfrac{L}{g}}.\nonumber \]
If \( θ_{max}\) is small, then \( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) is small. We claim that when \( k\) is small, this is a good estimate. To justify this claim, consider
\[ \int ^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
Since \( |\sin x|≤1\), this integral is bounded by
\[ \int ^{π/2}_0\left(\dfrac{1}{2}k^2+\dfrac{1.3}{2!2^2}k^4+⋯\right)\,dθ\;<\;\dfrac{π}{2}\left(\dfrac{1}{2}k^2+\dfrac{1⋅3}{2!2^2}k^4+⋯\right).\nonumber \]
Furthermore, it can be shown that each coefficient on the right-hand side is less than \( 1\) and, therefore, that this expression is bounded by
\( \dfrac{πk^2}{2}(1+k^2+k^4+⋯)=\dfrac{πk^2}{2}⋅\dfrac{1}{1−k^2}\),
which is small for \( k\) small.
b. For larger values of \( θ_{max}\), we can approximate \( T\) by using more terms in the integrand. By using the first two terms in the integral, we arrive at the estimate
\[ T≈4\sqrt{\frac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ\right)\,dθ=2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right).\nonumber \]
The applications of Taylor series in this section are intended to highlight their importance. In general, Taylor series are useful because they allow us to represent known functions using polynomials, thus providing us a tool for approximating function values and estimating complicated integrals. In addition, they allow us to define new functions as power series, thus providing us with a powerful tool for solving differential equations.
Key Concepts
- The binomial series is the Maclaurin series for \( f(x)=(1+x)^r\). It converges for \( |x|<1\).
- Taylor series for functions can often be derived by algebraic operations with a known Taylor series or by differentiating or integrating a known Taylor series.
- Power series can be used to solve differential equations.
- Taylor series can be used to help approximate integrals that cannot be evaluated by other means.
Glossary
- binomial series
- the Maclaurin series for \( f(x)=(1+x)^r\); it is given by \(\displaystyle (1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯\) for \( |x|<1\)
- non-elementary integral
- an integral for which the antiderivative of the integrand cannot be expressed as an elementary function


