1.8: Vector-Valued Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Now that we are familiar with vectors and their operations, we can begin discussing functions whose values are vectors.
Definition 1.10
A vector-valued function of a real variable is a rule that associates a vector f(t) with a real number t, where t is in some subset D of R1 (called the domain of f). We write f: D→R3 to denote that f is a mapping of D into R3.
For example, f(t)=ti+t2j+t3k is a vector-valued function in R3, defined for all real numbers t. We would write f : R→R3. At t=1 the value of the function is the vector i + j + k, which in Cartesian coordinates has the terminal point (1,1,1).
A vector-valued function of a real variable can be written in component form as
f(t)=f1(t)i+f2(t)j+f3(t)k
or in the form
f(t)=(f1(t),f2(t),f3(t))
for some real-valued functions f1(t),f2(t),f3(t), called the component functions of f. The first form is often used when emphasizing that f(t) is a vector, and the second form is useful when considering just the terminal points of the vectors. By identifying vectors with their terminal points, a curve in space can be written as a vector-valued function.
Example 1.35
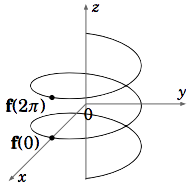
Define f: R→R3 by f(t)=(cost,sint,t). This is the equation of a helix (see Figure 1.8.1). As the value of t increases, the terminal points of f(t) trace out a curve spiraling upward. For each t, the x− and y−coordinates of f(t) are x=cost and y=sint, so
x2+y2=cos2t+sin2t=1
Thus, the curve lies on the surface of the right circular cylinder x2+y2=1.
It may help to think of vector-valued functions of a real variable in R3 as a generalization of the parametric functions in R2 which you learned about in single-variable calculus. Much of the theory of real-valued functions of a single real variable can be applied to vector-valued functions of a real variable. Since each of the three component functions are real-valued, it will sometimes be the case that results from single-variable calculus can simply be applied to each of the component functions to yield a similar result for the vector-valued function. However, there are times when such generalizations do not hold (see Exercise 13). The concept of a limit, though, can be extended naturally to vector-valued functions, as in the following definition.
Definition 1.11
Let f(t) be a vector-valued function, let a be a real number and let c be a vector. Then we say that the limit of f(t) as t approaches a equals c, written as limt→af(t)=c, if limt→a‖f(t)−c‖=0. If f(t)=(f1(t),f2(t),f3(t)), then
limt→af(t)=(limt→af1(t),limt→af2(t),limt→af3(t))
provided that all three limits on the right side exist.
The above definition shows that continuity and the derivative of vector-valued functions can also be defined in terms of its component functions.
Definition 1.12
Let f(t)=(f1(t),f2(t),f3(t)) be a vector-valued function, and let a be a real number in its domain. Then f(t) is continuous at a if limt→af(t)=f(a). Equivalently, f(t) is continuous at a if and only if f1(t),f2(t), and f3(t) are continuous at a.
The derivative of f(t) at a, denoted by f′(a) or dfdt(a), is the limit
f′(a)=limh→0f(a+h)−f(a)h
if that limit exists. Equivalently, f′(a)=(f1′(a),f2′(a),f3′(a)), if the component derivatives exist. We say that f(t) is differentiable at a if f′(a) exists.
Recall that the derivative of a real-valued function of a single variable is a real number, representing the slope of the tangent line to the graph of the function at a point. Similarly, the derivative of a vector-valued function is a tangent vector to the curve in space which the function represents, and it lies on the tangent line to the curve (see Figure 1.8.2).
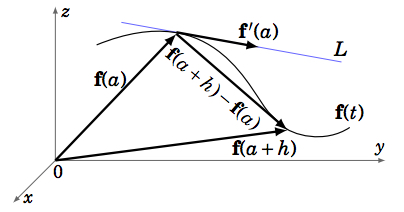
Example 1.36
Let f(t)=(cost,sint,t). Then f′(t)=(−sint,cost,1) for all t. The tangent line L to the curve at f(2π)=(1,0,2π) is L=f(2π)+sf′(2π)=(1,0,2π)+s(0,1,1), or in parametric form: x=1,y=s,z=2π+s for −∞<s<∞.
A scalar function is a real-valued function. Note that if u(t) is a scalar function and f(t) is a vector-valued function, then their product, defined by (uf)(t)=u(t)f(t) for all t, is a vector-valued function (since the product of a scalar with a vector is a vector).
The basic properties of derivatives of vector-valued functions are summarized in the following theorem.
Theorem 1.20
Let f(t) and g(t) be differentiable vector-valued functions, let u(t) be a differentiable scalar function, let k be a scalar, and let c be a constant vector. Then
- ddt(c)=0
- ddt(kf)=kdfdt
- ddt(f+g)=dfdt+dgdt
- ddt(f−g)=dfdt−dgdt
- ddt(uf)=dudtf+udfdt
- ddt(f·g)=dfdt·g+f·dgdt
- ddt(f×g)=dfdt×g+f×dgdt
Proof
The proofs of parts (a)-(e) follow easily by differentiating the component functions and using the rules for derivatives from single-variable calculus. We will prove part (f), and leave the proof of part (g) as an exercise for the reader.
(f) Write f(t)=(f1(t),f2(t),f3(t)) and g(t)=(g1(t),g2(t),g3(t)), where the component functions f1(t),f2(t),f3(t),g1(t),g2(t),g3(t) are all differentiable real-valued functions. Then
ddt(f(t)·g(t))=ddt(f1(t)g1(t)+f2(t)g2(t)+f3(t)g3(t))=ddt(f1(t)g1(t))+ddt(f2(t)g2(t))+ddt(f3(t)g3(t))=df1dt(t)g1(t)+f1(t)dg1dt(t)+df2dt(t)g2(t)+f2(t)dg2dt(t)+df3dt(t)g3(t)+f3(t)dg3dt(t)=(df1dt(t),df2dt(t),df3dt(t))·(g1(t),g2(t),g3(t))+(f1(t),f2(t),f3(t))·(dg1dt(t),dg2dt(t),dg3dt(t))=dfdt(t)·g(t)+f(t)·dgdt(t) for all t.
◻
Example 1.37
Suppose f(t) is differentiable. Find the derivative of ‖f(t)‖.
Since ‖f(t)‖ is a real-valued function of t, then by the Chain Rule for real-valued functions, we know that ddt‖f(t)‖2=2‖f(t)‖ddt‖f(t)‖.
But ‖f(t)‖2=f(t)·f(t), so ddt‖f(t)‖2=ddt(f(t)·f(t)). Hence, we have
2‖f(t)‖ddt‖f(t)‖=ddt(f(t)·f(t))=f′(t)·f(t)+f(t)·f′(t) by Theorem 1.20(f), so=2f′(t)·f(t), so if ‖f(t)‖≠0 thenddt‖f(t)‖=f′(t)·f(t)‖f(t)‖
We know that ‖f(t)‖ is constant if and only if ddt‖f(t)‖=0 for all t. Also, f(t)⊥f′(t) if and only if f′(t)·f(t)=0. Thus, the above example shows this important fact:
If ‖f(t)‖≠0, then ‖f(t)‖ is constant if and only if f(t)⊥f′(t) for all t.
This means that if a curve lies completely on a sphere (or circle) centered at the origin, then the tangent vector f′(t) is always perpendicular to the position vector f(t).
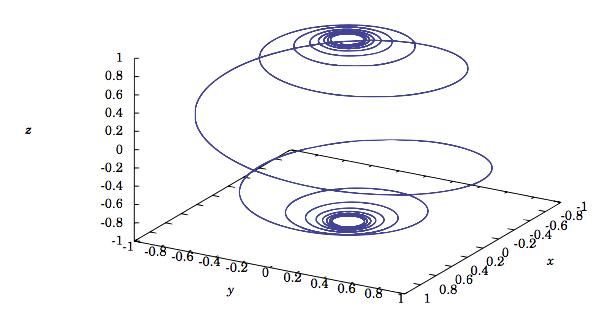
Example 1.38
The spherical spiral f(t)=(cost√1+a2t2,sint√1+a2t2,−at√1+a2t2), for a≠0.
Figure 1.8.3 shows the graph of the curve when a=0.2. In the exercises, the reader will be asked to show that this curve lies on the sphere x2+y2+z2=1 and to verify directly that f′(t)·f(t)=0 for all t.
Just as in single-variable calculus, higher-order derivatives of vector-valued functions are obtained by repeatedly differentiating the (first) derivative of the function:
f′′(t)=ddtf′(t),f′′′(t)=ddtf′′(t),...,dnfdtn=ddt(dn−1fdtn−1) (for n=2,3,4,...)
We can use vector-valued functions to represent physical quantities, such as velocity, acceleration, force, momentum, etc. For example, let the real variable t represent time elapsed from some initial time (t=0), and suppose that an object of constant mass m is subjected to some force so that it moves in space, with its position (x,y,z) at time t a function of t. That is, x=x(t),y=y(t),z=z(t) for some real-valued functions x(t),y(t),z(t). Call r(t)=(x(t),y(t),z(t)) the position vector of the object. We can define various physical quantities associated with the object as follows:
position:r(t)=(x(t),y(t),z(t))velocity:v(t)=˙r(t)=r′(t)=drdt=(x′(t),y′(t),z′(t))acceleration:a(t)=˙v(t)=v′(t)=dvdt=¨r(t)=r′′(t)=d2rdt2=(x′′(t),y′′(t),z′′(t))momentum:p(t)=mv(t)force:F(t)=˙p(t)=p′(t)=dpdt (Newton’s Second Law of Motion)
The magnitude ‖v(t)‖ of the velocity vector is called the speed of the object. Note that since the mass m is a constant, the force equation becomes the familiar F(t)=ma(t).
Example 1.39
Let r(t)=(5cost,3sint,4sint) be the position vector of an object at time t≥0. Find its (a) velocity and (b) acceleration vectors.
Solution
- v(t)=˙r(t)=(−5sint,3cost,4cost)
- a(t)=˙v(t)=(−5cost,−3sint,−4sint)
Note that ‖r(t)‖=√25cos2t+25sin2t=5 for all t, so by Example 1.37 we know that r(t)·˙r(t)=0 for all t (which we can verify from part (a)). In fact, ‖v(t)‖=5 for all t also. And not only does r(t) lie on the sphere of radius 5 centered at the origin, but perhaps not so obvious is that it lies completely within a circle of radius 5 centered at the origin. Also, note that a(t)=−r(t). It turns out (see Exercise 16) that whenever an object moves in a circle with constant speed, the acceleration vector will point in the opposite direction of the position vector (i.e. towards the center of the circle).
Recall from Section 1.5 that if r1,r2 are position vectors to distinct points then r1+t(r2−r1) represents a line through those two points as t varies over all real numbers. That vector sum can be written as (1−t)r1+tr2. So the function l(t)=(1−t)r1+tr2 is a line through the terminal points of r1 and r2, and when t is restricted to the interval [0,1] it is the line segment between the points, with l(0)=r1 and l(1)=r2.
In general, a function of the form f(t)=(a1t+b1,a2t+b2,a3t+b3) represents a line in R3. A function of the form f(t)=(a1t2+b1t+c1,a2t2+b2t+c2,a3t2+b3t+c3) represents a (possibly degenerate) parabola in R3.
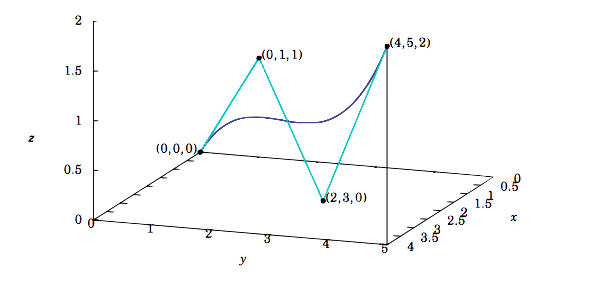
Example 1.40: Bézier curves
Bézier curves are used in Computer Aided Design (CAD) to approximate the shape of a polygonal path in space (called the Bézier polygon or control polygon). For instance, given three points (or position vectors) b0,b1,b2 in R3, define
b10(t)=(1−t)b0+tb1b11(t)=(1−t)b1+tb2b20(t)=(1−t)b10(t)+tb11(t)=(1−t)2b0+2t(1−t)b1+t2b2
for all real t. For t in the interval [0,1], we see that b10(t) is the line segment between b0 and b1, and b11(t) is the line segment between b1 and b2. The function b20(t) is the Bézier curve for the points b0,b1,b2. Note from the last formula that the curve is a parabola that goes through b0 (when t=0) and b2 (when t=1).
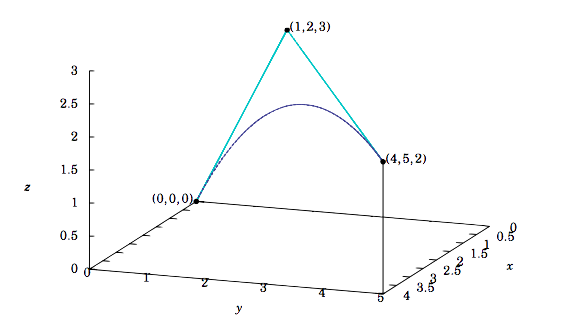
As an example, let b0=(0,0,0),b1=(1,2,3), and b2=(4,5,2). Then the explicit formula for the Bézier curve is b20(t)=(2t+2t2,4t+t2,6t−4t2), as shown in Figure 1.8.4, where the line segments are b10(t) and b11(t), and the curve is b20(t).
In general, the polygonal path determined by n≥3 noncollinear points in R3 can be used to define the Bézier curve recursively by a process called repeated linear interpolation. This curve will be a vector-valued function whose components are polynomials of degree n−1, and its formula is given by de Casteljau’s algorithm. In the exercises, the reader will be given the algorithm for the case of n=4 points and asked to write the explicit formula for the Bézier curve for the four points shown in Figure 1.8.5.